以下是UC San Diego的ECON 120B的midterm exam的题目的简单解析
Name _________________________________
Student ID# _________________________________
midterm exam EXAM
ECON 120B, ECONOMETRICS
Gordon Dahl
UC San Diego
Instructions: You will have 100 minutes to complete the exam. Details on how to submit your
answers are discussed in the instructions for the Technology Quiz and so are not repeated here.
The only differences are: (i) you will have 100 minutes for the final exam (instead of 70 minutes)
and (ii) the start time of the exam is as stated in the class announcement on Canvas (you must
begin at the stated start time, as the 100 minute limit begins then). Failure to follow those
instructions could result in a failing score on the final.
Write your answers as clearly and concisely as possible, and feel free to use mathematical
expressions in your explanations. Show your derivations, reasoning, and calculations on the short
answer questions. You will not receive full credit on the short answer questions unless you show
your work.
You may use one page of notes, written on one side of a regular sized piece of paper.
These notes must be prepared by you and written in your handwriting. One thing you may want
to include on your sheet of notes are the two tables on the next page. These tables will not be
included on the exam, but contains all of the critical values you will need to answer the exam
questions.
You may use the built-in calculator which appears in Respondus LockDown Browser.
You may not use any books (electronic or paper), class notes (electronic or paper), or any other
internet, electronic, or paper resources.
You may not receive any help on the exam or discuss/share the questions with anyone.
You may not use your phone during the exam, except to convert your answers to a pdf file and
upload them to Gradescope.
You may not use any scratch paper. The only paper you should have is the Blank Answer Sheet
which you will write your answers on. All of your answers must appear in the designated areas.
Good luck!2
Distribution Tables
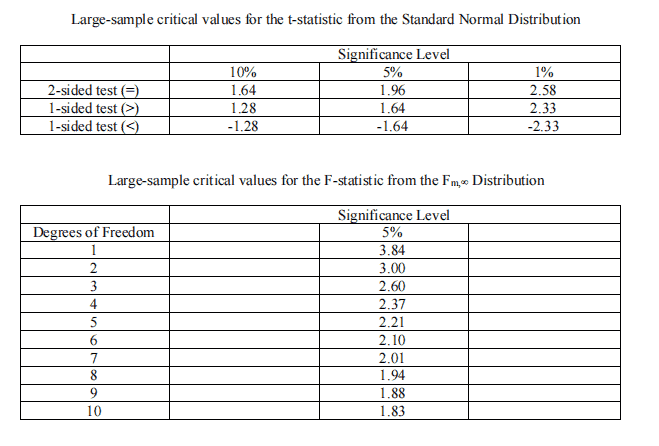
Useful notes:
(1) Point totals for each question are given in brackets. The actual exam may have more or fewer
points. Use the point totals for the questions to help you allocate your time effectively.
(2) The actual exam may have multiple choice questions, true/false questions or a combination of
these types of questions.
(3) The actual exam will have one or more short answer questions. Make sure to show your work
and explain your steps for full credit.
(4) Make sure to review any announcements on Canvas which provide further details regarding
the final exam.
Econometrics代写经济代写第一题
Multiple Choice: Choose the one alternative that best completes the statement or answers the question.
1.1) An estimate is
A) unbiased if its expected value equals the population value
B) a number
C) another word for estimator
D) efficient if it has the smallest variance
1.2) Under imperfect multicollinearity
A) the OLS estimator is biased even in large samples
B) two or more of the regressors are highly correlated
C) the OLS estimator cannot be computed
D) the error terms are highly, but not perfectly correlated, across different observations
1.3) When there are omitted variables in the regression, which are determinants of the dependent variable, then
A) the OLS estimator is biased if the omitted variable is correlated with the included variable
B) you cannot measure the effect of the omitted variable, but the estimators of your included
variables are unaffected
C) this will always bias the OLS estimator of the included variable
D) this has no effect on the estimator of your included variable because the other variable is not
included
1.4) The interpretation of the slope coefficient in the model $\ln \left(Y_{i}\right)=\beta_{0}+\beta_{1} X_{i}+u_{i}$ is:
A) a $1 \%$ increase in $X$ is associated with a change in $Y$ of $.01 \times \beta_{1}$
B) an increase in $X$ by one unit is associated with a $100 \times \beta_{1} \%$ change in $Y$
C) an increase in $X$ by one unit is associated with a $\beta_{1}$ change in $Y$
D) a $1 \%$ increase in $X$ is associated with a $\beta_{1} \%$ change in $Y$
基本的概念题
Econometrics代写经济代写第二题
(a) Let $X_{i} i=1, \ldots, n$ denote a sequence of random variables which are independent and identically distributed. Write down a formula for the sample mean.
(b) Consider the regression model $Y_{i}=\beta_{0}+\beta_{1} X_{i}+u_{i},$ and assume the first three least squares assumptions hold. State the Gauss Markov Theorem, including any additional assumptions needed for the theorem to hold (beyond the first three least squares assumptions).
(c) Define the average treatment effect (ATE) in terms of potential outcomes.
还是概念题,比如第一题sample mean就是
the distribution of the population, with mean ${ }^{\mu}$ and standard deviation ${ }^{\sigma}$. The sample mean is defined to be $\bar{x}=\frac{1}{n}\left(X_{I}+X_{2}+\cdots+X_{n}\right)$
Econometrics代写经济代写第三题
Consider the regression equation $Y_{i}=\beta_{0}+\beta_{1} X_{i}+u_{i} .$ Show that $\hat{\beta}_{1}=r_{X Y}\left(\frac{s_{Y}}{s_{X}}\right),$ where $r_{x y}$ is the sample correlation between $X$ and $Y,$ and $s_{x}$ and $s_{Y}$ are the sample standard deviations.
一些代数变形
Econometrics代写经济代写第四题
Females, on average, are shorter and weigh less than males. One of your friends tells you that in addition, females will weigh less for a given height. To test this hypothesis, you use a simple random sample to collect the height and weight of 59 female and 54 male students at UCSD. A regression of the weight on a constant, height, and a binary variable which takes a value of one for females and is zero otherwise, yields the following result:
weight $_{i}=-229.21-6.36 \times$ female $_{i}+5.58 \times$ height $_{i} \quad \mathrm{R}^{2}=0.50, \mathrm{RMSE}=20.99$
Where weight is weight measured in pounds, female takes a value of 1 for females and is 0 otherwise, and height is measured in inches.
(a) What is the literal interpretation of the intercept term? Does a negative intercept term imply a problem with the regression you ran? Explain.
(b) Is the estimated coefficient for height significantly different from zero at the $5 \%$ confidence level? Show your work.
(c) You decide to rescale the height variable by subtracting 5 feet (or 60 inches) from the original variable height. Will this change the estimated intercept term if you re-run the regression with this rescaled variable instead? Explain.
(d) Suppose you collected this data by having students fill out a survey. If men are not good at remembering their height, so that you have a noisy measure of their height, what problems (if any) does this create?
(e) Come up with one omitted variable which you think would create a bias for the estimated height coefficient. Which direction would this omitted variable bias the coefficient? Explain your reasoning
假设检验和置信区间的应用题
Econometrics代写经济代写第五题
A subsample from the Current Population Survey (a survey the U.S. government uses to calculate official statistics) is taken on weekly earnings of individuals, their age, and their gender. You have read in the news that women make 70 cents for every $\$ 1$ that men earn. To examine this hypothesis, you first regress weekly earnings on a constant and a binary variable female, which takes on a value of 1 for females and 0 otherwise. The regression results are:
earn $_{i}=570.70-170.72 \times$ female $_{i} \quad \mathrm{R}^{2}=0.084, \mathrm{RMSE}=282.12, \mathrm{~N}=1740$
(a) What are the mean earnings of males and females in this sample?
(b) A classmate argues that you should control for education. He breaks education into 3 mutually exclusive and exhaustive categories: high school dropout or less, high school graduate, and at least one year of college. He says you should add three dummy variables into the model, one for each category. Is this good advice? Explain.
You decide to control for age (in years) in your regression results because you hypothesize that older people earn more on average than younger people, but at a decreasing rate as they age. This regression output is as follows:
$$
\begin{array}{l}
\text { earn }_{i}=323.70-169.78 \times \text { female }_{i}+15.15 \times \text { age }_{i}-.021 \times \text { age }^{2} \text { i } \\
\mathrm{R}^{2}=0.135, \mathrm{RMSE}=274.45, \mathrm{~N}=1,740
\end{array}
$$
(c) What words do the initials RMSE stand for? Interpret the RMSE.
(d) How much more, on average, does a 30-year-old male make per year in your sample compared to a 25 -year-old female? (note: you do not need to simplify your answer)
(e) Assuming homoskedasticity, test whether age and $a g e^{2}$ are jointly significant. Show your work. To help get you started, the formula for the homoskedasticity only F statistic is:
$$
\frac{\left(R_{\text {unrestricted }}^{2}-R_{\text {restricted }}^{2}\right) / q}{\left(1-R_{\text {unrestricted }}^{2}\right) /(n-k-1)}
$$
线性回归的应用题

E-mail: [email protected] 微信:shuxuejun
Econometrics代写经济代写ECON 120B代写请认准uprivateta
更多统计代写案例请参考另外一份统计代写案例
uprivate™是一个服务全球中国留学生的专业代写公司
专注提供稳定可靠的北美、澳洲、英国代写服务
专注于数学,统计,金融,经济,计算机科学,物理的作业代写服务