| Multiplication and addition are defined in the most obvious way subject to the convention that $i^{2}=-1$. Thus, $$ (a+i b)+(c+i d)=(a+c)+i(b+d) $$ and $$ (a+i b)(c+i d)=a c+i a d+i b c+i^{2} b d=(a c-b d)+i(b c+a d) $$ Every non zero complex number, $a+i b$, with $a^{2}+b^{2} \neq 0$, has a unique multiplicative inverse. $$ \frac{1}{a+i b}=\frac{a-i b}{a^{2}+b^{2}}=\frac{a}{a^{2}+b^{2}}-i \frac{b}{a^{2}+b^{2}} $$ You should prove the following theorem. Theorem 2.13.1 The complex numbers with multiplication and addition defined as above form a field satisfying all the field axioms listed on Page 9 . The field of complex numbers is denoted as $\mathrm{C}$. An important construction regarding complex numbers is the complex conjugate denoted by a horizontal line above the number. It is defined as follows. $$ \overline{a+i b} \equiv a-i b $$ What it does is reflect a given complex number across the $x$ axis. Algebraically, the following formula is easy to obtain. $$ (\overline{a+i b})(a+i b)=a^{2}+b^{2} . $$ Definition 2.13.2 Define the absolute value of a complex number as follows. $$ |a+i b| \equiv \sqrt{a^{2}+b^{2}} $$ Thus, denoting by $z$ the complex number $z=a+i b$, $$ |z|=(z \bar{z})^{1 / 2} $$ Be sure to verify the last claim in this definition. With this definition, it is important to note the following. Be sure to verify this. It is not too hard but you need to do it. Remark $2.13 .3:$ Let $z=a+i b$ and $w=c+i d .$ Then $|z-w|=\sqrt{(a-c)^{2}+(b-d)^{2}}$. Thus the distance between the point in the plane determined by the ordered pair, $(a, b)$ and the ordered pair $(c, d)$ equals $|z-w|$ where $z$ and $w$ are as just described. For example, consider the distance between $(2,5)$ and $(1,8)$. From the distance formula which you should have seen in either algebra or calculus, this distance is defined ass $$ \sqrt{(2-1)^{2}+(5-8)^{2}}=\sqrt{10} $$ On the other hand, letting $z=2+i 5$ and $w=1+i 8, z-w=1-i 3$ and so $$ (z-w)(\overline{z-w})=(1-i 3)(1+i 3)=10 $$ so $|z-w|=\sqrt{10}$, the same thing obtained with the distance formula. Notation 2.13.4 From now on I will sometimes use the symbol $\mathrm{F}$ to denote either $\mathbb{C}$ or $\mathbb{R}$, ruther than fussing over which one is meant becuuse it often does not make any difference. |
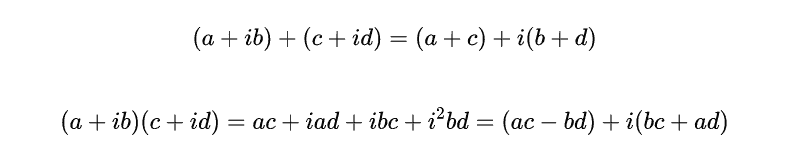

real analysis代写analysis 2, analysis 3请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
代写
隐藏