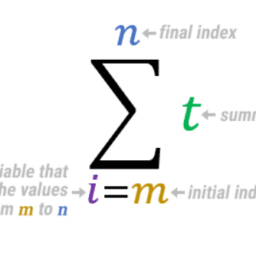| Proposition 2.14.5 The greatest common divisor of $\left{p_{1}(\lambda), \cdots, p_{\mathrm{m}}(\lambda)\right}$ exists and is characterized as the monic polynomial of smallest degree equal to an expression of the form $$ \sum_{k=1}^{m} a_{k}(\lambda) p_{k}(\lambda), \text { the } a_{k}(\lambda) \text { being polynomials. } $$ Proof: First I need show that if $q(\lambda)$ is monic of the above form with smallest degree, then it is the greatest common divisor. If $q(\lambda)$ fails to divide $p_{k}(\lambda)$, then $p_{k}(\lambda)=q(\lambda) l(\lambda)+r(\lambda)$ where the degree of $r(\lambda)$ is smaller than the degree of $q(\lambda)$. Thus, $$ r(\lambda)=p_{k}(\lambda)-l(\lambda) \sum_{k=1}^{m} a_{k}(\lambda) p_{k}(\lambda) $$ which violates the condition that $q(\lambda)$ has smallest degree. Thus $q(\lambda) / p_{k}(\lambda)$ for each $k$. If $\hat{q}(\lambda)$ divides each $p_{k}(\lambda)$ then it must divide $q(\lambda)$ because $q(\lambda)$ is given by $2.1$. Hence $q(\lambda)$ is the greatest common divisor. Next, why does such greatest common divisor exist? Simply pick the monic polynomial which has smallest degree which is of the form $\sum_{k-1}^{m} a_{k}(\lambda) p_{k}(\lambda)$. Then from what was just shown, it is the greatest common divisor. Proposition 2.14.6 Let $p(\lambda)$ be a polynomial. Then there are polynomials $p_{1}(\lambda)$ such that $$ p(\lambda)=a \prod_{i=1}^{m} p_{i}(\lambda)^{m_{i}} $$ where $m_{1} \in \mathbb{N}$ and $\left{p_{1}(\lambda), \cdots, p_{m}(\lambda)\right}$ are monic and relatively prime or else there is no polynomial of degree larger than 0 which divides $p(\lambda)$. Proof: If there is no polynomial of degree larger than 0 dividing $p(\lambda)$, then we are done. Simply pick $a$ such that $p(\lambda)$ is monic. Otherwise $p(\lambda)=a p_{1}(\lambda) p_{2}(\lambda)$ where $p_{1}(\lambda)$ is monic and each has degree at least 1. These could be the same polynomial. If some nonconstant polynomial divides each $p_{1}(\lambda)$, factor further. Continue doing this. Eventually the process must end with a factorization as described in $2.2$ because the degrees of the factors are decreasing- $2.15$ The Cauchy Schwarz Inequality This fundamental inequality takes several forms. I will present the version first given by Cauchy although I am not sure if the proof is the same. Proposition 2.15.1 Let $z_{j}, w_{j}$ be complex numbers. Then $$ \left|\sum_{j=1}^{\mathrm{P}} z_{j} \overline{w_{j}}\right| \leq\left(\sum_{j=1}^{p}\left|z_{j}\right|^{2}\right)^{1 / 2}\left(\sum_{j=1}^{\mathrm{P}}\left|w_{j}\right|^{2}\right)^{1 / 2} $$ Proof: First note that $\sum_{j-1}^{p} z_{j} \overline{z_{j}}=\sum_{j-1}^{p}\left|z_{j}\right|^{2} \geq 0 .$ Next, if $a+i b$ is a complex number, consider $\theta=1$ if both $a, b$ are zero and $\theta=\frac{a-1 b}{\sqrt{a^{2}+b^{2}}}$ if the complex number is not zero. Thus, in either case, there exists a complex number $\theta$ such that $|\theta|=1$ and $\theta(a+i b)=|a+i b| \equiv \sqrt{a^{2}+b^{2}}$. Now let $|\theta|=1$ and $$ \theta \sum_{j=1}^{p} z_{j} \overline{w_{j}}=\left|\sum_{j=1}^{p} z_{j} \overline{w_{j}}\right| $$ |
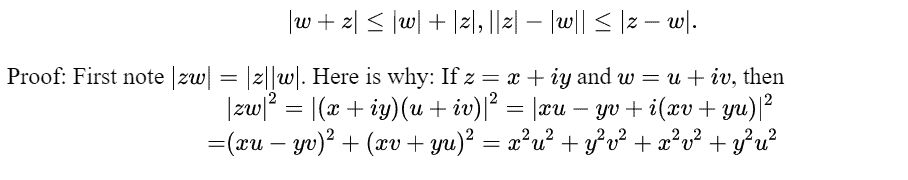

real analysis代写analysis 2, analysis 3请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
代写
隐藏