| Definition 2.7.1 A set is well ordered if every nonempty subset $S$, contains a smallest element $z$ having the property that $z \leq x$ for all $x \in S$. Axiom 2.7.2 Any set of integers larger than a given number is well ordened. In particular, the natural numbers defined as $\mathbb{N} \equiv{1,2, \cdots}$ is well ordered. The above axiom implies the principle of mathematical induction. Theorem $2.7 .3$ (Mathematical indwction) A set $S \subseteq \mathbb{Z}$, having the property that $a \in S$ and $n+1 \in S$ whenever $n \in S$ contains all integers $x \in \mathbb{Z}$ such that $x \geq a$. Proof: Let $T \equiv([a, \infty) \cap \mathbb{Z}) \backslash S$. Thus $T$ consists of all integers larger than or equal to $a$ which are not in $S$. The theorem will be proved if $T=\emptyset .$ If $T \neq \emptyset$ then by the well ordering principle, there would have to exist a smallest element of $T$, denoted as $b$. It must be the case that $b>a$ since by definition, $a \notin T$. Then the integer, $b-1 \geq a$ and $b-1 \notin S$ because if $b-1 \in S$, then $b-1+1=b \in S$ by the assumed property of $S$. Therefore, $b-1 \in([a, \infty) \cap \mathbb{Z}) \backslash S=T$ which contradicts the choice of $b$ as the smallest element of $T$. ( $b-1$ is smaller.) Since a contradiction is obtained by assuming $T \neq \emptyset$, it must be the case that $T=\emptyset$ and this says that everything in $[a, \infty) \cap \mathbb{Z}$ is also in $S$. Mathematical induction is a very useful device for proving theorems about the integers. Example 2.7.4 Prove by induction that $\sum_{k-1}^{n} k^{2}=\frac{n(n+1)(2 n+1)}{6}$. By inspection, if $n=1$ then the formuls is true. The sum yields 1 and so does the formula on the right. Suppose this formuls is valid for some $n \geq 1$ where $n$ is an integer. Then $$ \sum_{k=1}^{n+1} k^{2}=\sum_{k=1}^{n} k^{2}+(n+1)^{2}=\frac{n(n+1)(2 n+1)}{6}+(n+1)^{2} $$ The step going from the first to the second equality is based on the assumption that the formula is true for $n$. This is called the induction hypothesis. Now simplify the expression in the second line, $$ \frac{n(n+1)(2 n+1)}{6}+(n+1)^{2} . $$This equals $(n+1)\left(\frac{n(2 n+1)}{6}+(n+1)\right)$ and $$ \frac{n(2 n+1)}{6}+(n+1)=\frac{6(n+1)+2 n^{2}+n}{6}=\frac{(n+2)(2 n+3)}{6} $$ Therefore, $$ \sum_{k=1}^{n+1} k^{2}=\frac{(n+1)(n+2)(2 n+3)}{6}=\frac{(n+1)((n+1)+1)(2(n+1)+1)}{6} $$ showing the formula holds for $n+1$ whenever it holds for $n$. This proves the formula by mathematical induction. Example $2.7 .5$ Show that for all $n \in \mathbb{N}, \frac{1}{2} \cdot \frac{3}{4} \ldots \frac{2 n-1}{2 n}<\frac{1}{\sqrt{2 n+1}}$. If $n=1$ this reduces to the statement that $\frac{1}{2}<\frac{1}{\sqrt{3}}$ which is obviously true. Suppose then that the inequality holds for $n$. Then $$ \frac{1}{2} \cdot \frac{3}{4} \cdots \frac{2 n-1}{2 n} \cdot \frac{2 n+1}{2 n+2}<\frac{1}{\sqrt{2 n+1}} \frac{2 n+1}{2 n+2}=\frac{\sqrt{2 n+1}}{2 n+2} $$ The theorem will be proved if this last expression is less than $\frac{1}{\sqrt{2 n+3}}$. This happens if and only if $$ \left(\frac{1}{\sqrt{2 n+3}}\right)^{2}=\frac{1}{2 n+3}>\frac{2 n+1}{(2 n+2)^{2}} $$ which occurs if and only if $(2 n+2)^{2}>(2 n+3)(2 n+1)$ and this is clearly true which may be seen from expanding both sides. This proves the inequality. Lets review the process just used. If $S$ is the set of integers at least as large as 1 for which the formula holds, the first step was to show $1 \in S$ and then that whenever $n \in S$, it follows $n+1 \in S$. Therefore, by the principle of mathematical induction, $S$ contains $[1, \infty) \cap \mathbb{Z}$, all positive integers. In doing an inductive proof of this sort, the set, $S$ is normally not mentioned. One just verifies the steps above. First show the thing is true for some $a \in \mathbb{Z}$ and then verify that whenever it is true for $m$ it follows it is also true for $m+1$. When this has been done, the theorem has been proved for all $m \geq a$. |
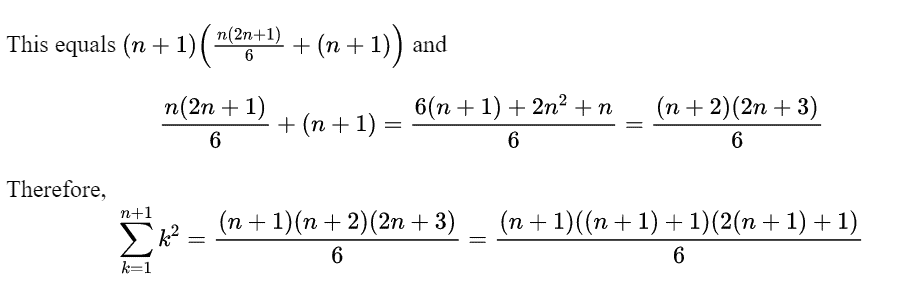

real analysis代写analysis 2, analysis 3请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
代写
隐藏