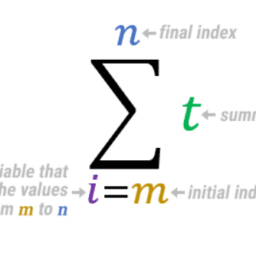0 0

By admin 数学代写 2022年2月22日

Proof: Consider the first claim. If the indicated set equals $\emptyset$, then sup $(S)-\delta$ is an upper bound for $S$ which is smaller than sup $(S)$, contrary to the definition of $\sup (S)$ as the least upper bound. In the second claim, if the indicated set equals $\emptyset$, then inf $(S)+\delta$ would be a lower bound which is larger than inf $(S)$ contrary to the definition of inf $(S)$.
The wonderful thing about sup is that you can switch the order in which they occur. The same thing holds for inf. It is also convenient to generalize the notion of sup and inf so that we don’t have to worry about whether it is a real number.
Definition 2.10.4 Let $f(a, b) \in[-\infty, \infty]$ for $a \in A$ and $b \in B$ where $A, B$ are nonempty sets which means that $f(a, b)$ is either a number, $\infty$, or $-\infty$. The symbol, $+\infty$ is interpreted as a point out at the end of the number line which is larger than every real number. Of course there is no such number. That is why it is called $\infty$. The symbol, $-\infty$ is interpreted similarly. Then sup $_{a \in A} f(a, b)$ means sup $\left(S_{b}\right)$ where $S_{b} \equiv{f(a, b): a \in A}$. A similar convention holds for inf.
Unlike limits, you can take the sup in different orders, same for inf.
Lemma 2.10.5 Let $f(a, b) \in[-\infty, \infty]$ for $a \in A$ and $b \in B$ where $A, B$ are sets. Then
$$
\sup {a \in A} \sup {b \in B} f(a, b)=\sup {b \in B} \sup {a \in A} f(a, b) .
$$
Also, you can replace sup with inf.
Proof: Note that for all $a, b, f(a, b) \leq \sup {b \in B} \sup {a \in A} f(a, b)$ and therefore, for all $a, \sup {b \in B} f(a, b) \leq \sup {b \in B} \sup {a \in A} f(a, b)$. Therefore, $$ \sup {a \in A} \sup {b \in B} f(a, b) \leq \sup {b \in B} a \in A \atop f(a, b) .
$$
Repeat the same argument interchanging $a$ and $b$, to get the conclusion of the lemms. Similar considerations give the same result for inf.
$2.11$ Existence of Roots
What is $\sqrt[5]{7}$ and does it even exist? You can ask for it on your calculator and the calculator will give you a number which multiplied by itself 5 times will yield a number which is close to 7 but it isn’t exactly right. Why should there exist a number which works exactly? Every one you find, appears to be some sort of approximation at best. If you can’t produce one, why should you believe it is even there? The following is an argument that roots exist. You fill in the details of the argument. Brsically, roots exist in anslysis because of completeness of the real line. Here is a lemms.
Lemma 2.11.1 Suppose $n \in \mathbb{N}$ and $a>0$. Then if $x^{n}-a \neq 0$, there exists $\delta>0$ such that whenever
$$
y \in(x-\delta, x+\delta)
$$
it follows $y^{n}-a \neq 0$ and has the same sign as $x^{n}-a$.
Proof: Using the binomial theorem, $y^{n}=(y-x+x)^{n}$
$$
=\sum_{k=0}^{n-1}\left(\begin{array}{c}
n \
k
\end{array}\right)(y-x)^{n-k} x^{k}+x^{n}
$$
Let $|y-x|<1$. Then using the triangle inequality, it follows that for $|y-x|<1$,
$$
\left|y^{n}-x^{n}\right| \leq|y-x| \sum_{k=0}^{n-1}\left(\begin{array}{c}
n \
k
\end{array}\right)|x|^{k} \equiv C|x-y|
$$

证明：考虑第一个主张。如果指示集等于$\emptyset$，则sup $(S)-\delta$ 是$S$ 的上限，它小于sup $(S)$，这与$\sup (S) 的定义相反$ 作为最小上限。在第二个声明中，如果指示的集合等于 $\emptyset$，那么 inf $(S)+\delta$ 将是一个大于 inf $(S)$ 的下界，这与 inf $(S) 的定义相反美元。 sup 的美妙之处在于您可以切换它们出现的顺序。同样的事情也适用于 inf。推广 sup 和 inf 的概念也很方便，这样我们就不必担心它是否是实数。定义 2.10.4 令 $f(a, b) \in[-\infty, \infty]$ 对于 $a \in A$ 和 $b \in B$ 其中 $A, B$ 是非空集，这意味着 $ f(a, b)$ 是一个数字、$\infty$ 或 $-\infty$。符号 $+\infty$ 被解释为数轴末端的一个点，它比每个实数都大。当然没有这样的数字。这就是为什么它被称为$\infty$。符号 $-\infty$ 的解释类似。然后 sup $_{a \in A} f(a, b)$ 表示 sup $\left(S_{b}\right)$ 其中 $S_{b} \equiv\{f(a, b): a \在 A\}$。类似的约定适用于 inf。与限制不同，您可以按不同的顺序接受 sup，inf 也是如此。引理 2.10.5 令 $f(a, b) \in[-\infty, \infty]$ 为 $a \in A$ 和 $b \in B$ 其中 $A, B$ 是集合。然后 $$ \sup _{a \in A} \sup _{b \in B} f(a, b)=\sup _{b \in B} \sup _{a \in A} f(a, b) 。 $$ 此外，您可以将 sup 替换为 inf。证明：注意对于所有 $a, b, f(a, b) \leq \sup _{b \in B} \sup _{a \in A} f(a, b)$ 因此，对于所有 $ a, \sup_{b \in B} f(a, b) \leq \sup_{b \in B} \sup_{a \in A} f(a, b)$。所以， $$ \sup _{a \in A} \sup _{b \in B} f(a, b) \leq \sup _{b \in B} a \in A \atop f(a, b) 。 $$ 重复相同的论点，交换 $a$ 和 $b$，得到引理的结论。类似的考虑对 inf 给出了相同的结果。 $2.11$ 根的存在什么是 $\sqrt[5]{7}$，它甚至存在吗？你可以在你的计算器上要求它，计算器会给你一个数字，它自己乘以 5 次将得到一个接近 7 的数字，但它并不完全正确。为什么应该存在一个完全有效的数字？你发现的每一个，似乎充其量只是某种近似值。如果你不能生产一个，你为什么要相信它甚至在那里？以下是根存在的论点。您填写论点的详细信息。归根结底，由于实线的完整性，分析中存在根源。这是一个lemms。引理 2.11.1 假设 $n \in \mathbb{N}$ 和 $a>0$。那么如果 $x^{n}-a \neq 0$，则存在 $\delta>0$ 使得无论何时 $$ y \in(x-\delta, x+\delta) $$ 它跟在 $y^{n}-a \neq 0$ 之后，并且与 $x^{n}-a$ 具有相同的符号。证明：使用二项式定理，$y^{n}=(y-x+x)^{n}$ $$ =\sum_{k=0}^{n-1}\left(\begin{array}{c} n \\ ķ \end{数组}\right)(y-x)^{n-k} x^{k}+x^{n} $$ 令 $|y-x|

real analysis代写analysis 2, analysis 3请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。

代写隐藏