| Theorem $2.13 .5$ Let $z, w \in \mathbb{C}$. Then $$ |w+z| \leq|w|+|z|,|| z|-| w|| \leq|z-w| . $$ Proof: First note $|z w|=|z||w|$. Here is why: If $z=x+i y$ and $w=u+i v$, then $$ \begin{aligned} &|z w|^{2}=|(x+i y)(u+i v)|^{2}=|x u-y v+i(x v+y u)|^{2} \ =&(x u-y v)^{2}+(x v+y u)^{2}=x^{2} u^{2}+y^{2} v^{2}+x^{2} v^{2}+y^{2} u^{2} \end{aligned} $$ Now look at the right side. $$ |z|^{2}|w|^{2}=(x+i y)(x-i y)(u+i v)(u-i v)=x^{2} u^{2}+y^{2} v^{2}+x^{2} v^{2}+y^{2} u^{2} $$ the same thing. Thus the rest of the proof goes just as before with real numbers. Using the results of Problem 6 on Page 36 , the following holds. $$ \begin{aligned} |z+w|^{2} &=(z+w)(\bar{z}+\bar{w})=z \bar{z}+z \bar{w}+w \bar{z}+w \bar{w} \ &=|z|^{2}+|w|^{2}+z \bar{w}+\overline{\overline{w z z}} \ &=|z|^{2}+|w|^{2}+2 \operatorname{Re} z \bar{w} \ & \leq|z|^{2}+|w|^{2}+2|z \bar{w}|=|z|^{2}+|w|^{2}+2|z||w| \ &=(|z|+|w|)^{2} \end{aligned} $$ and so $|z+w| \leq|z|+|w|$ as claimed. The other inequality follows as before. $$ |z| \leq|z-w|+|w| $$ and so $|z|-|w| \leq|z-w|=|w-z|$. Now do the same argument switching the roles of $z$ and $w$ to conclude $$ |z|-|w| \leq|z-w|,|w|-|z| \leq|z-w| $$ which implies the desired inequality. Since $\mathbb{R} \subseteq \mathbb{C}$ and the absolute value is consistently defined, the inequality holds also on $\mathbb{R}$. 2.14 Dividing Polynomials It will be very important to be able to work with polynomials, especially in subjects like linear algebra and with the technique of partial fractions. It is surprising how useful this junior high material will be. In this section, a polynomial is an expression. Later, the expression will be used to define a function. These two ways of looking at a polynomial are very different. Definition 2.14.1 A polynomial is an expression of the form $p(\lambda)=$ $$ a_{n} \lambda^{\mathrm{n}}+a_{n-1} \lambda^{n-1}+\cdots+a_{1} \lambda+a_{0}, $$ $a_{n} \neq 0$ where the $a_{1}$ are (real or complex) numbers. Two polynomials are equal means that the coefficients match for each power of $\lambda$. The degree of a polynomial is the largest power of $\lambda$. Thus the degree of the above polynomial is $n$. Addition of polynomials is defined in the usual way as is multiplication of two polynomials. The leading term in the above polynomial is $a_{n} \lambda^{n}$. The coefficient of the leading term is called the leading coefficient. It is called a monic polynomial if $a_{n}=1$. A root of a polynomial $p(\lambda)$ is $\mu$ such that $p(\mu)=0$. This is also called a zero. |
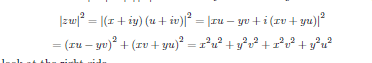

real analysis代写analysis 2, analysis 3请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
代写
隐藏