0 0

By admin 数学代写 2022年2月23日

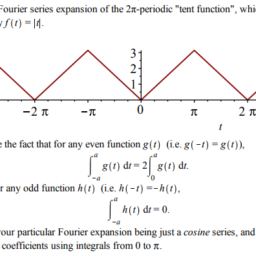
$8.10$ Multiplication of Power Series
Next consider the problem of multiplying two power series.
Theorem 8.10.1 Let $\sum_{n=0}^{\infty} a_{n}(x-a)^{n}$ and $\sum_{n=0}^{\infty} b_{n}(x-a)^{n}$ be two power series having radii of convergence $r_{1}$ and $r_{2}$, both positive. Then
$$
\left(\sum_{n=0}^{\infty} a_{n}(x-a)^{n}\right)\left(\sum_{n=0}^{\infty} b_{n}(x-a)^{n}\right)=\sum_{n=0}^{\infty}\left(\sum_{k=0}^{n} a_{k} b_{n-k}\right)(x-a)^{n}
$$
whenever $|x-a|<r \equiv \min \left(r_{1}, r_{2}\right) .$
Proof: By Theorem 8.1.3 both series converge absolutely if $|x-a|<r$. Therefore, by Theorem 5.5.6
$$
\begin{gathered}
\left(\sum_{n=0}^{\infty} a_{n}(x-a)^{n}\right)\left(\sum_{n=0}^{\infty} b_{n}(x-a)^{n}\right)= \
\sum_{n=0}^{\infty} \sum_{k=0}^{n} a_{k}(x-a)^{k} b_{n-k}(x-a)^{n-k}=\sum_{n=0}^{\infty}\left(\sum_{k=0}^{n} a_{k} b_{n-k}\right)(x-a)^{n}
\end{gathered}
$$
2 Surprisingly, this function is very important to those who use modern techniques to study differential equations. One needs to consider test functions which have the property they have infinitely many derivatives but vanish outside of some interval. The theory of complex variables can be used to show there are no examples of such functions if they have a valid power series expansion. It even becomes enough of them, and it is this very example which is used to show this.

The significance of this theorem in terms of applications is that it states you can multiply power series just as you would multiply polynomials and everything will be all right on the common interval of convergence. This is called the Cauchy product. This theorem can be used to find Taylor series which would perhaps be hard to find without it. Here is an example. Example $8.10 .2$ Find the Toylor series for $e^{x}$ sin $x$ centered at $x=0$. From the above theorem the result should be All that is required is to multiply $$ (\overbrace{1+x+x^{2}}^{2}+\left(-\frac{1}{3 !}+\frac{1}{2 !}\right) x^{3}+\cdots $$ $1+\frac{x^{2}}{2 !}+\frac{x^{3}}{3 !} \cdots$
You can continue this way and get the following to a few more terms.
$$
x+x^{2}+\frac{1}{3} x^{3}-\frac{1}{30} x^{5}-\frac{1}{90} x^{6}-\frac{1}{630} x^{7}+\cdots
$$
I don’t see a pattern in these coefficients but I can go on generating them as long as I want. (In practice this tends to not be very long.) I also know the resulting power series will converge for all $x$ because both the series for $e^{x}$ and the one for $\sin x$ converge for all $x$.
Example 8.10.3 Find the Taylor series for $\tan x$ centered at $x=0$.
Lets suppose it has a Taylor series $a_{0}+a_{1} x+a_{2} x^{2}+\cdots$ Then
$$
x+x^{2}+\frac{1}{3} x^{3}-\frac{1}{30} x^{5}-\frac{1}{90} x^{6}-\frac{1}{630} x^{7}+\cdots
$$
I don’t see a pattern in these coefficients but I can go on generating them as long as I want. (In practice this tends to not be very long.) I also know the resulting power series will converge for all $x$ because both the series for $e^{x}$ and the one for $\sin x$ converge for all $x$.
Example 8.10.3 Find the Taylor series for $\tan x$ centered at $x=0$.
Lets suppose it has a Taylor series $a_{0}+a_{1} x+a_{2} x^{2}+\cdots \cdot$ Then
$\left.x^{2}+\cdots\right)(\overbrace{1-}^{ }$
Using the above, $a_{0}=0, a_{1} x=x$ so $$ a_{1}=1,\left(0\left(\frac{-1}{2}\right)+a_{2}\right) x^{2} $$ so $a_{2}=0 .$ $\left(a_{3}-\frac{a_{1}}{2}\right) x^{3}=\frac{-1}{3 !} x^{3}$
$x$ so $=1,\left(0\left(\frac{-1}{2}\right)+a_{2}\right) x^{2}=0$
so $a_{3}-\frac{1}{2}=-\frac{1}{6}$ so $a_{3}=\frac{1}{3}$. Clearly one can continue in this manner. Thus the first several terms of the power series for tan are
$$
\tan x=x+\frac{1}{3} x^{3}+\cdots
$$
$=\left(x-\frac{x^{3}}{3 !}+\frac{x^{5}}{5 !}\right.$ 3 $=0$ in this manner. and two yielding
You can go on calculating these terms and find the next two yield $$ \tan x=x+\frac{1}{3} x^{3}+\frac{2}{15} x^{5}+\frac{17}{315} x^{7}+\cdots $$
8.11. EXERCISES
173
This is a very significant technique because, as you see, there does not appear to be a very simple pattern for the coefficients of the power series for tan $x$. Of course there are some issues here about whether $\tan x$ even has a power series, but if it does, the above must be it. In fact, $\tan (x)$ will have a power series valid on some interval centered at 0 and this becomes completely obvious when one uses methods from complex analysis but it isn’t too obvious at this point. If you are interested in this issue, read the last section of the chapter. Note also that what has been accomplished is to divide the power series for $\sin x$ by the power series for $\cos x$ just like they were polynomials.

$8.10$ 幂级数的乘法
接下来考虑乘以两个幂级数的问题。
定理 8.10.1 令 $\sum_{n=0}^{\infty} a_{n}(xa)^{n}$ 和 $\sum_{n=0}^{\infty} b_{n}(xa )^{n}$ 是两个幂级数，其收敛半径为 $r_{1}$ 和 $r_{2}$，均为正数。然后
$$
\left(\sum_{n=0}^{\infty} a_{n}(xa)^{n}\right)\left(\sum_{n=0}^{\infty} b_{n}(xa )^{n}\right)=\sum_{n=0}^{\infty}\left(\sum_{k=0}^{n} a_{k} b_{nk}\right)(xa)^ {n}
$$
每当 $|x-a|<r \equiv \min \left(r_{1}, r_{2}\right) .$
证明：根据定理 8.1.3，如果 $|x-a|<r$，则两个级数绝对收敛。因此，由定理 5.5.6
$$
\开始{聚集}
\left(\sum_{n=0}^{\infty} a_{n}(xa)^{n}\right)\left(\sum_{n=0}^{\infty} b_{n}(xa )^{n}\右)= \
\sum_{n=0}^{\infty} \sum_{k=0}^{n} a_{k}(xa)^{k} b_{nk}(xa)^{nk}=\sum_{n =0}^{\infty}\left(\sum_{k=0}^{n} a_{k} b_{nk}\right)(xa)^{n}
\结束{聚集}
$$
2 令人惊讶的是，这个函数对于那些使用现代技术研究微分方程的人来说非常重要。需要考虑具有无限多导数但在某个区间之外消失的特性的测试函数。如果它们具有有效的幂级数展开式，则复变量理论可用于表明不存在此类函数的示例。它甚至变得足够了，正是这个例子被用来证明这一点。

这个定理在应用方面的意义在于它表明你可以乘幂级数，就像你乘多项式一样，并且在共同的收敛区间上一切都会好起来的。这称为柯西积。这个定理可以用来找到泰勒级数，没有它可能很难找到。这是一个例子。示例 $8.10 .2$ 求以 $x=0$ 为中心的 $e^{x}$ sin $x$ 的托勒级数。根据上述定理，结果应该是只需将 $$ (\overbrace{1+x+x^{2}}^{2}+\left(-\frac{1}{3 !}+ \frac{1}{2 !}\right) x^{3}+\cdots $$ $1+\frac{x^{2}}{2 !}+\frac{x^{3}}{3 ! } \cdots$
您可以继续这种方式并获得以下几个术语。
$$
x+x^{2}+\frac{1}{3} x^{3}-\frac{1}{30} x^{5}-\frac{1}{90} x^{6}- \frac{1}{630} x^{7}+\cdots
$$
我没有在这些系数中看到模式，但我可以根据需要继续生成它们。（实际上，这往往不会很长。）我也知道得到的幂级数将对所有 $x$ 收敛，因为 $e^{x}$ 的级数和 $\sin x$ 的级数都收敛于所有$x$。
例 8.10.3 求以 $x=0$ 为中心的 $\tan x$ 的泰勒级数。
假设它有一个泰勒级数 $a_{0}+a_{1} x+a_{2} x^{2}+\cdots$ 那么
$$
x+x^{2}+\frac{1}{3} x^{3}-\frac{1}{30} x^{5}-\frac{1}{90} x^{6}- \frac{1}{630} x^{7}+\cdots
$$
我没有在这些系数中看到模式，但我可以根据需要继续生成它们。（实际上，这往往不会很长。）我也知道得到的幂级数将对所有 $x$ 收敛，因为 $e^{x}$ 的级数和 $\sin x$ 的级数都收敛于所有$x$。
例 8.10.3 求以 $x=0$ 为中心的 $\tan x$ 的泰勒级数。
假设它有一个泰勒级数 $a_{0}+a_{1} x+a_{2} x^{2}+\cdots \cdot$ 那么
$\left.x^{2}+\cdots\right)(\overbrace{1-}^{ }$
使用上述，$a_{0}=0, a_{1} x=x$ 所以 $$ a_{1}=1,\left(0\left(\frac{-1}{2}\right)+ a_{2}\right) x^{2} $$ 所以 $a_{2}=0 .$ $\left(a_{3}-\frac{a_{1}}{2}\right) x^{ 3}=\frac{-1}{3 !} x^{3}$
$x$ 所以 $=1,\left(0\left(\frac{-1}{2}\right)+a_{2}\right) x^{2}=0$
所以 $a_{3}-\frac{1}{2}=-\frac{1}{6}$ 所以 $a_{3}=\frac{1}{3}$。显然，人们可以以这种方式继续。因此 tan 幂级数的前几项是
$$
\tan x=x+\frac{1}{3} x^{3}+\cdots
$$
$=\left(x-\frac{x^{3}}{3 !}+\frac{x^{5}}{5 !}\right.$ 3 $=0$ 以这种方式。两个产生
您可以继续计算这些项并找到接下来的两个收益率 $$ \tan x=x+\frac{1}{3} x^{3}+\frac{2}{15} x^{5}+\frac {17}{315} x^{7}+\cdots $$
8.11。练习
173
这是一项非常重要的技术，因为如您所见，对于 tan $x$ 的幂级数的系数似乎没有一个非常简单的模式。当然这里有一些关于$\tan x$是否有幂级数的问题，但如果有的话，上面的肯定就是它了。事实上，$\tan (x)$ 将有一个在以 0 为中心的某个区间上有效的幂级数，当使用复杂分析的方法时，这一点变得非常明显，但在这一点上还不太明显。如果您对此问题感兴趣，请阅读本章的最后一节。还要注意，已经完成的是将 $\sin x$ 的幂级数除以 $\cos x$ 的幂级数，就像它们是多项式一样。