物理代考| Bound States 量子力学代写
物理代写
3.5 bound States
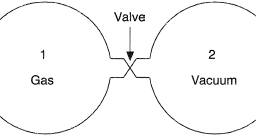
As another application of the one-dimensional Schrödinger equation, consider the lowest-energy ground state in an attractive square-well potential
$$
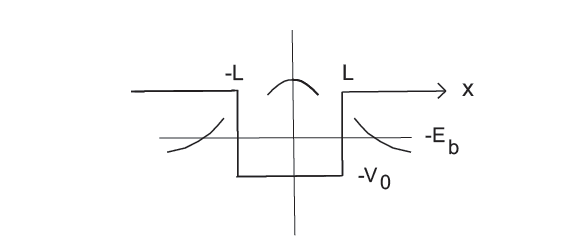
V(x)=-V_{0} \quad ;-L0$. We are looking for a bound state with (see Fig. 3.5)
$$
E=-E_{b}<0 \quad \text {; bound state } $$ The ground state will be symmetric, and so we only have to consider $x>0$.
Fig. 3.5 Bound ground state in a square-well potential in one dimension. Here we make the minus signs explicit, with $V=-V_{0}<0$, and $E=-E_{b}<0$. We are looking for the symmetric ground-state eigenfunction, with no nodes and minimum curvature. ${ }^{2}$ See, for example, [Walecka (2008)]. 20 Introduction to Quantum Mechanics Inside the potential, we want the symmetric solution with minimum curvature, and so $\psi(x)=a \cos \left(\kappa_{i} x\right) \quad ; xL \
\cdots^{2} & 2 m & &
\end{array}
$$
yet, match the logarithmic derivative, which is the ratio of the derivative to the function, since one then gets rid of the amplitudes. Thus, with a change in sign, $$ \kappa_{i} \tan \left(\kappa_{i} L\right)=\kappa_{o} \quad \text {; eigenvalue equation (3.30) } $$ $$ \kappa_{o}^{2}=\frac{2 m}{\hbar^{2}} E_{b} $$ Now match the wave functions and their derivatives at et, match the logarithmic derivative, which is the ratio of the function, since one then gets rid of the amplitudes. hange in sign, $$ \kappa_{i} \tan \left(\kappa_{i} L\right)=\kappa_{o} \quad \text {; eigenvalue equation } $$ Given $V_{0}$, this transcendental eigenvalue equation must be solved $\mathrm{n}$ cally for $E_{b}$. Fortunately, we can readily extract two limiting cases:
(1) Suppose $V_{0}$ is very large, then $E_{b}$ will also be very large, and so will the r.h.s. of Eq. (3.30). Now adjust $V_{0}$. Start with $V_{0}=E_{b}$, in which case the l.h.s. vanishes. Move $V_{0}$ away from $E_{b}$. By the time one gets to $\left(\kappa_{i} L\right)=\pi / 2$, one will have found a solution to Eq. (3.30) since the l.h.s. is infinite at that point. Hence, as $V_{0} \rightarrow \infty$ one has
$$
E_{b}=V_{0}-\frac{\hbar^{2}}{2 m}\left(\frac{\pi}{2 L}\right)^{2} \quad ; V_{0} \rightarrow \infty
$$
When the well is very deep, the ground state looks just like the ground state of a particle in a one-dimensional box of length $2 L$.
(2) Suppose $V_{0}$ goes to zero. $E_{b}$ then also goes to zero, and the r.h.s. of Eq. (3.30) is very small. $^{3}$ Again, start with $V_{0}=E_{b}$ in which case the l.h.s. vanishes. Move $V_{0}$ away from $E_{b}$ a little. An expansion of the l.h.s. of Eq. (3.30) for small $\left(\kappa_{i} L\right)$ gives
$\kappa_{i}\left(\kappa_{i} L\right)=\kappa_{o}$
${ }^{3}$ The wave function now falls off only very slowly outside of the potential.
物理代考
3.5 约束状态
作为一维薛定谔方程的另一个应用,考虑有吸引力的方形阱势中的最低能量基态
$$
V(x)=-V_{0} \quad ;-L0$。我们正在寻找一个绑定状态(见图 3.5)
$$
E=-E_{b}<0 \quad \text {;绑定状态 } $$ 基态将是对称的,因此我们只需要考虑 $x>0$。
图 3.5 一维方阱电位中的束缚基态。这里我们明确减号,$V=-V_{0}<0$,$E=-E_{b}<0$。我们正在寻找没有节点和最小曲率的对称基态特征函数。 ${ }^{2}$ 例如,参见 [Walecka (2008)]。 20 量子力学导论 在势内,我们想要曲率最小的对称解,所以 $\psi(x)=a \cos \left(\kappa_{i} x\right) \quad ; xL \
\cdots^{2} & 2 m & &
\结束{数组}
$$
然而,匹配对数导数,它是导数与函数的比率,因为这样就可以摆脱幅度。因此,随着符号的变化,$$ \kappa_{i} \tan \left(\kappa_{i} L\right)=\kappa_{o} \quad \text {;特征值方程 (3.30) } $$ $$ \kappa_{o}^{2}=\frac{2 m}{\hbar^{2}} E_{b} $$ 现在匹配 et 处的波函数及其导数,匹配对数导数,它是函数的比率,因为然后摆脱了幅度。悬挂符号,$$ \kappa_{i} \tan \left(\kappa_{i} L\right)=\kappa_{o} \quad \text {;特征值方程 } $$ 给定 $V_{0}$,这个超越特征值方程必须用 $\mathrm{n}$ 求解 $E_{b}$。幸运的是,我们可以很容易地提取两种限制情况:
(1) 假设$V_{0}$ 很大,那么$E_{b}$ 也会很大,r.h.s. 也会很大。方程。 (3.30)。现在调整 $V_{0}$。从 $V_{0}=E_{b}$ 开始,在这种情况下,l.h.s.消失。将 $V_{0}$ 从 $E_{b}$ 移开。等到 $\left(\kappa_{i} L\right)=\pi / 2$ 时,就会找到方程的解。 (3.30) 自 l.h.s.在那一点上是无限的。因此,正如 $V_{0} \rightarrow \infty$ 有
$$
E_{b}=V_{0}-\frac{\hbar^{2}}{2 m}\left(\frac{\pi}{2 L}\right)^{2} \quad ; V_{0} \rightarrow \infty
$$
当井很深时,基态看起来就像一个粒子在长度为 $2 L$ 的一维盒子中的基态。
(2) 假设 $V_{0}$ 变为零。然后 $E_{b}$ 也归零,而 r.h.s.方程。 (3.30) 非常小。 $^{3}$ 再次以 $V_{0}=E_{b}$ 开头,在这种情况下,l.h.s.消失。将 $V_{0}$ 从 $E_{b}$ 移开一点。 l.h.s.的扩展方程。 (3.30) 对于小的 $\left(\kappa_{i} L\right)$ 给出
$\kappa_{i}\left(\kappa_{i} L\right)=\kappa_{o}$
${ }^{3}$ 现在波函数在势能之外非常缓慢地下降

3.1 薛定谔方程
让我们尝试扩展薛定谔方程来描述质量为 $m$ 的非相对论粒子在真实势 $V(x)$ 中运动。一个明显的方法是仅仅求助于我们的经典力学论点,并将汉密尔顿方程扩展为
$$
\frac{p^{2}}{2 m} \rightarrow \frac{p^{2}}{2 m}+V(x)
$$
让我们看看如果我们使用以下哈密顿量,我们之前的量子力学论证会发生什么
$$
H(p, x)=\frac{p^{2}}{2 m}+V(x) \quad ; \文本{汉密尔顿}
$$
我们将继续将薛定谔方程中的动量写为
$$
p=\frac{\hbar}{i} \frac{\partial}{\partial x} \quad ; \text {动量}
$$
汉密尔顿仍然是厄米特,因为真正的潜力是厄米特
$$
\int d x \psi^{}(x) V \psi(x)=\int d x[V \psi(x)]^{} \psi(x) \quad ; \text { 厄米特人 }
$$
然后分离的解决方案再次成为静止状态
$$
\Psi(
$$ $$ \Psi(x, t)=\psi(x) e^{-i E t / \hbar} $$ 其中 $E$ 是实际能量 $$ \frac{\int dx \psi^{ }(x) H \psi(x)}{\int dx|\psi(x)|^{2}}=E $$ 14 $\quad$ 量子力学导论 $$ \frac{\partial \rho (x, t)}{\partial t}+\frac{\partial S(x, t)}{\partial x}=0 $$ rhs 上的势能抵消方程。 (2.15) $$ \begin{array}{l}\left.1 \hbar^{}(x, t)[V \Psi(x, t)]-[V \Psi(x, t)]^ {} \Psi(x, t)\right}=0 \ \text { 因此概率连续性方程的论证 }\end{array} $$ 在哪里 $$ \开始{数组}{lrl} \rho(x, t) & =|\Psi(x, t)|^{2} & ; \text { 概率密度 } \ S(x, t) & =\frac{1}{2 m}\left{\Psi^{\star}(x, t) p \Psi(x, t)+[p \Psi(x, t )]^{} \Psi(x, t)\right}
\结束{数组}
$$
;概率通量
特别是,概率密度和通量在静止状态下仍然与时间无关
$$
\开始{对齐}
\rho(x) &=|\psi(x)|^{2} & ; \text { 静止状态 } \
S(x) &=\frac{1}{2 m}\left{\psi^{\star}(x) p \psi(x)+[p \psi(x)]^{*} \psi (x)\右}
\end{对齐}
$$
物理代考| Classical Optics量子力学代写 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
电磁学代考
物理代考服务:
物理Physics考试代考、留学生物理online exam代考、电磁学代考、热力学代考、相对论代考、电动力学代考、电磁学代考、分析力学代考、澳洲物理代考、北美物理考试代考、美国留学生物理final exam代考、加拿大物理midterm代考、澳洲物理online exam代考、英国物理online quiz代考等。
光学代考
光学(Optics),是物理学的分支,主要是研究光的现象、性质与应用,包括光与物质之间的相互作用、光学仪器的制作。光学通常研究红外线、紫外线及可见光的物理行为。因为光是电磁波,其它形式的电磁辐射,例如X射线、微波、电磁辐射及无线电波等等也具有类似光的特性。
大多数常见的光学现象都可以用经典电动力学理论来说明。但是,通常这全套理论很难实际应用,必需先假定简单模型。几何光学的模型最为容易使用。
相对论代考
上至高压线,下至发电机,只要用到电的地方就有相对论效应存在!相对论是关于时空和引力的理论,主要由爱因斯坦创立,相对论的提出给物理学带来了革命性的变化,被誉为现代物理性最伟大的基础理论。
流体力学代考
流体力学是力学的一个分支。 主要研究在各种力的作用下流体本身的状态,以及流体和固体壁面、流体和流体之间、流体与其他运动形态之间的相互作用的力学分支。
随机过程代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其取值随着偶然因素的影响而改变。 例如,某商店在从时间t0到时间tK这段时间内接待顾客的人数,就是依赖于时间t的一组随机变量,即随机过程