经济代写 |Decision trees and actions 微观经济学代写
经济代写
2.1. Perfect information. Before defining a decision situation in extensive form, we need to clarify what we mean by a partition.
DEFINITION III.1 (PARTITION). Let $M$ be any nonempty set. A partition of $M$ is a subset $\mathcal{P}{M}=\left{M{1}, \ldots, M_{k}\right}$ of the power set $2^{M}$ such that
hold. $B y \mathcal{P}{M}(m)$ we mean the element of $\mathcal{P}{M}$ that contains $m \in M$. The elements of partitions are often called components. A component with one element only is called a singleton.
Most of the time, a partition will not contain the empty set but we allow for this possibility.
EXERCISE III.1. Write down two partitions of $M:={1,2,3}$. Find $\mathcal{P}_{M}$ (1) in each case.
We begin by describing a decision situation. (This description is not a very formal definition but leans on the investment-marketing decision situation.)
DEfINITION III.2 (EXTENSIVE-FORM DECISION SITUATION). A decision situation (in extensive form and for perfect information) $\Delta=\left(V, u,\left(A_{d}\right)_{d \in D}\right)$ is given by
- a tree with node set $V$ where the nodes are often denoted by $v_{0}$, $v_{1}, \ldots$ together with
- links that connect the nodes, directly or indirectly.
Additionally:
34
III. DECISIONS IN EXTENSIVE FORM - A tree has an initial node $v_{0}$ and for every node $v$ thene exists exactly one trail (consisting of links) from $v_{0}$ to $v$ (see below). Trails are indicated by brackets \langle\rangle that contain at least two nodes.
- A trail is called maximal if it cannot be extended.
- The length of a trail is defined in the obvious manner (just go from one node to successor nodes and count the number of steps). The length of a tree is defined by its longest trail.
- $D$ is the set of non-terminal nodes that are also called decision nodes. $A_{d}$ is the set of actions that can be chosen at decision node d. Every link at $d$ corresponds to exactly one action. The set of all actions is defined by $A=\cup_{d \in D} A_{d}$.
- $E$ is the set of end nodes where a payoff function $u: E \rightarrow \mathbb{R}$ records the payoffs.
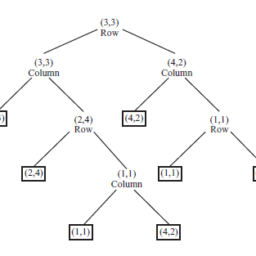
We have three decision nodes and six actions in the investment-marketing decision situation. The link from $v_{1}$ to $v_{3}$ in figure III.1 corresponds to action $M$ if the firm has chosen I at the first stage. Action M after action nI is a different link (the one from $v_{2}$ to $v_{5}$ ). Furthermore, observe $D=\left{v_{0}, v_{1}, v_{2}\right}$, $E=\left{v_{3}, v_{4}, v_{5}, v_{6}\right}, A_{v_{2}}={\mathrm{M}, \mathrm{nM}}, A={\mathrm{I}, \mathrm{nI}, \mathrm{M}, \mathrm{nM}} .$ The trail $\left\langle v_{0}, v_{3}\right\rangle$ has length 2 , while the length of trail $\left\langle v_{1}, v_{3}\right\rangle$ is 1 .
EXERCISE III.2. What is the length of the investment-marketing tree above? How about the absent minded driver (where you disregand the dotted line)? Indicate all the maximal trails in these two decision situations.
2.2. Imperfect information. The above definition refers to “perfect information”. This means that the decision maker knows the decision node at which he finds himself. In contrast, under “imperfect information” the decision maker does not know exactly the current decision node. We represent imperfect information by information sets that gather decision nodes between which the decision maker cannot distinguish. Therefore, the actions available at different nodes in an information set have to be the same. The absent-minded driver provides an example.
DEFINITION III.3 (INFORMATION PARTITION). A decision situation (in extensive form and for imperfect information) $\Delta=\left(V, u, I,\left(A_{d}\right){d \in D}\right)$ equals the one for perfect information with the following exception: There exists a partition I (called information partition) of the decision nodes $D$. The elements of I are called information sets (which are components of I). The actions at decision nodes belonging to the same information set have to be identical: $A{a}=A_{d^{\prime}}$ for all $d, d^{\prime} \in I(d)$.
2.1。完善的信息。在以广泛的形式定义决策情况之前,我们需要澄清分区的含义。
定义 III.1(分区)。令 $M$ 为任意非空集。 $M$ 的分区是幂集 $2^{M} 的子集 $\mathcal{P}{M}=\left{M{1}, \ldots, M_{k}\right}$ $ 这样
抓住。 $B y \mathcal{P}{M}(m)$ 我们指的是 $\mathcal{P}{M}$ 中包含 $m \in M$ 的元素。分区的元素通常称为组件。只有一个元素的组件称为单例。
大多数情况下,分区不会包含空集,但我们允许这种可能性。
练习 III.1。记下 $M:={1,2,3}$ 的两个分区。在每种情况下找到 $\mathcal{P}_{M}$ (1)。
我们首先描述一个决策情况。 (这个描述不是一个非常正式的定义,而是依赖于投资营销决策情况。)
定义 III.2(广泛形式的决策情况)。一个决策情况(广泛形式和完美信息)$\Delta=\left(V, u,\left(A_{d}\right)_{d \in D}\right)$ 由下式给出
- 具有节点集 $V$ 的树,其中节点通常由 $v_{0}$、$v_{1}、\ldots$ 和
- 直接或间接连接节点的链接。
此外:
34
三、广泛形式的决定 - 一棵树有一个初始节点 $v_{0}$ 并且对于每个节点 $v$ 都存在从 $v_{0}$ 到 $v$ 的一条路径(由链接组成)(见下文)。路径由包含至少两个节点的括号 \langle\rangle 指示。
- 如果一条路径不能扩展,则称为最大路径。
- 路径的长度以显而易见的方式定义(只需从一个节点到后继节点并计算步数)。树的长度由其最长的路径定义。
- $D$ 是非终端节点的集合,也称为决策节点。 $A_{d}$ 是可以在决策节点 d 处选择的动作集。 $d$ 处的每个链接都对应一个操作。所有动作的集合由 $A=\cup_{d \in D} A_{d}$ 定义。
- $E$ 是支付函数 $u: E \rightarrow \mathbb{R}$ 记录支付的端节点集。
在投资营销决策情境中,我们有三个决策节点和六个动作。如果公司在第一阶段选择了 I,则图 III.1 中从 $v_{1}$ 到 $v_{3}$ 的链接对应于行动 $M$。动作 nI 之后的动作 M 是不同的链接(从 $v_{2}$ 到 $v_{5}$ 的链接)。此外,观察 $D=\left{v_{0}, v_{1}, v_{2}\right}$, $E=\left{v_{3}, v_{4}, v_{5 }, v_{6}\right}, A_{v_{2}}={\mathrm{M}, \mathrm{nM}}, A={\mathrm{I}, \mathrm{nI} , \mathrm{M}, \mathrm{nM}} .$ 轨迹 $\left\langle v_{0}, v_{3}\right\rangle$ 的长度为 2 ,而轨迹 $\left\ 的长度角度 v_{1}, v_{3}\right\rangle$ 是 1 。
练习 III.2。上面的投资营销树的长度是多少?心不在焉的司机(你无视虚线)怎么样?指出这两种决策情况下的所有最大轨迹。
2.2.信息不完善。上述定义指的是“完美信息”。这意味着决策者知道他所在的决策节点。相反,在“不完全信息”下,决策者并不确切知道当前的决策节点。我们通过收集决策者无法区分的决策节点的信息集来表示不完全信息。因此,信息集中不同节点可用的动作必须相同。心不在焉的司机提供了一个例子。
定义 III.3(信息分区)。一个决策情况(扩展形式和不完全信息)$\Delta=\left(V, u, I,\left(A_{d}\right){d \in D}\right)$ 等于完美信息,但有以下例外:存在决策节点$D$的分区I(称为信息分区)。 I 的元素称为信息集(它们是 I 的组成部分)。属于同一信息集的决策节点的动作必须相同:$A{a}=A_{d^{\prime}}$ for all $d, d^{\prime} \in I(d)$ .
经济代考
微观经济学又称个体经济学,小经济学,是宏观经济学的对称。 微观经济学主要以单个经济单位( 单个的生产者、单个的消费者、单个市场的经济活动)作为研究对象,分析单个生产者如何将有限的资源分配在各种商品的生产上以取得最大的利润;单个消费者如何将有限的收入分配在各种商品的消费上以获得最大的满足。

其他相关科目课程代写:组合学Combinatorics集合论Set Theory概率论Probability组合生物学Combinatorial Biology组合化学Combinatorial Chemistry组合数据分析Combinatorial Data Analysis
my-assignmentexpert愿做同学们坚强的后盾,助同学们顺利完成学业,同学们如果在学业上遇到任何问题,请联系my-assignmentexpert™,我们随时为您服务!
微观经济学 是研究人们和企业在资源分配、商品和服务交易价格等方面做出的决策。它考虑税收、法规和政府立法。
计量经济学代考
计量经济学是以一定的经济理论和统计资料为基础,运用数学、统计学方法与电脑技术,以建立经济计量模型为主要手段,定量分析研究具有随机性特性的经济变量关系的一门经济学学科。 主要内容包括理论计量经济学和应用经济计量学。 理论经济计量学主要研究如何运用、改造和发展数理统计的方法,使之成为经济关系测定的特殊方法。
相对论代考
相对论(英語:Theory of relativity)是关于时空和引力的理论,主要由愛因斯坦创立,依其研究对象的不同可分为狭义相对论和广义相对论。 相对论和量子力学的提出给物理学带来了革命性的变化,它们共同奠定了现代物理学的基础。
编码理论代写
编码理论(英语:Coding theory)是研究编码的性质以及它们在具体应用中的性能的理论。编码用于数据压缩、加密、纠错,最近也用于网络编码中。不同学科(如信息论、电机工程学、数学、语言学以及计算机科学)都研究编码是为了设计出高效、可靠的数据传输方法。这通常需要去除冗余并校正(或检测)数据传输中的错误。
编码共分四类:[1]
数据压缩和前向错误更正可以一起考虑。
复分析代考
学习易分析也已经很冬年了,七七八人的也续了圧少的书籍和论文。略作总结工作,方便后来人学 Đ参考。
复分析是一门历史悠久的学科,主要是研究解析函数,亚纯函数在复球面的性质。下面一昭这 些基本内容。
(1) 提到复变函数 ,首先需要了解复数的基本性左和四则运算规则。怎么样计算复数的平方根, 极坐标与 $x y$ 坐标的转换,复数的模之类的。这些在高中的时候囸本上都会学过。
(2) 复变函数自然是在复平面上来研究问题,此时数学分析里面的求导数之尖的运算就会很自然的 引入到复平面里面,从而引出解析函数的定义。那/研究解析函数的性贡就是关楗所在。最关键的 地方就是所谓的Cauchy一Riemann公式,这个是判断一个函数是否是解析函数的关键所在。
(3) 明白解析函数的定义以及性质之后,就会把数学分析里面的曲线积分 $a$ 的概念引入复分析中, 定义几乎是一致的。在引入了闭曲线和曲线积分之后,就会有出现复分析中的重要的定理: Cauchy 积分公式。 这个是易分析的第一个重要定理。