my-assignmentexpert™ Economics 经济学作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 $100 \%$ 原创。my-assignmentexpert™, 最高质量的ECON经济学作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于economics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此经济作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在经济学作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的经济代写服务。我们的专家在经济学 代写方面经验极为丰富,各种economics相关的作业也就用不着 说。
我们提供的econ代写服务范围广, 其中包括但不限于:
- 微观经济学
- 货币银行学
- 数量经济学
- 宏观经济学
- 经济统计学
- 经济学理论
- 商务经济学
- 计量经济学
- 金融经济学
- 国际经济学
- 健康经济学
- 劳动经济学
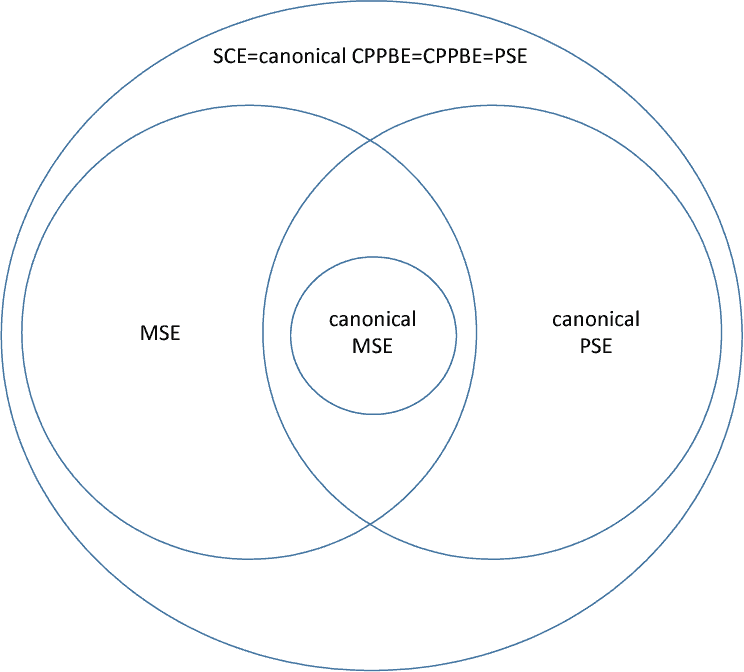
Econ经济作业代写Economics代考|The revelation principle
- In a message game, a principal asks for information about the players’ types so that the action sets equal the type sets, $\left(M_{i}=\right) A_{i}:=$ $T_{i}$.
We now consider any mechanism $(M, \zeta)$ and a strategy combination $s^{}$ for the corresponding message game. $s^{}$ can (but need not) be an equilibrium. With the help of $s^{*}$ we can transform $(M, \zeta)$ into a direct mechanism.
DEFINITION XVIII.7 (DERIVED DIRECT MECHANISM). Let $(M, \zeta)$ be a mechanism for $(N, T, \tau, Z, u)$ and let $s^{}$ be a strategy combination of the corresponding message game $\Gamma=\left(N, M, T, \tau,\left(u_{i}\right)_{i \in N}\right)$. Then, $\left(T, \zeta^{s^{}}\right)$ defined by
$$
\begin{aligned}
\zeta^{s^{}} &=\zeta \circ s^{}: \
T & \rightarrow Z \
t & \mapsto \zeta^{s^{}}(t)=\zeta\left(s^{}(t)\right)
\end{aligned}
$$
is the direct mechanism derived from $(M, \zeta)$ by $s^{}$. In the introductory section, we present a suitable example. There, the mechanism ( $T$, first-price auction) is used to derive the mechanism ( $T$, half-price auction) by the half-bid strategy combination $s^{}$. Figure XVIII.2 depicts $\zeta^{s^{}}$ as the composition $\zeta \circ s^{}$ of functions $\zeta$ and $s^{*}$ where
- first, $s^{}$ is applied to a type combination $t \in T$ to yield the message combination $s^{}(t) \in M$ and
- second, $\zeta$ is applied to that message combination so that we obtain an outcome $\zeta\left(s^{*}(t)\right) \in Z$.
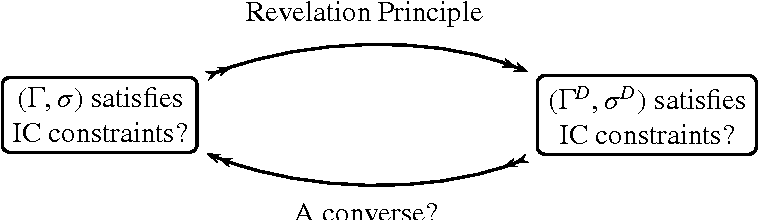
We now turn to the celebrated revelation principle. We give a proof for implementation via dominant strategies (theorem XVIII.1) and via Bayesian equilibria (theorem XVIII.2).
- 在消息游戏中,委托人询问有关玩家类型的信息,以便动作集等于类型集,(米一世=)一种一世:= 吨一世.
我们现在考虑任何机制(米,G)和一个策略组合 $s^{ }F○r吨H和C○rr和sp○nd一世nG米和ss一种G和G一种米和.s^{ }C一种n(b你吨n和和dn○吨)b和一种n和q你一世一世一世br一世你米.在一世吨H吨H和H和一世p○Fs^{*}在和C一种n吨r一种nsF○r米(M, \zeta)$ 转化为直接机制。
定义 XVIII.7(衍生直接机制)。让(米,G)成为一种机制(ñ,吨,τ,和,你)让 $s^{ }b和一种s吨r一种吨和G和C○米b一世n一种吨一世○n○F吨H和C○rr和sp○nd一世nG米和ss一种G和G一种米和\Gamma=\left(N, M, T, \tau,\left(u_{i}\right)_{i \in N}\right).吨H和n,\left(T, \zeta^{s^{ }}\right)d和F一世n和db和$
\begin{对齐}
\zeta^{s^{ }} &=\zeta \circ s^{ }: \
T & \rightarrow Z \
t & \mapsto \zeta^{s^{ }}(t)= \zeta\left(s^{ }(t)\right)
\end{aligned}
$$
是从(米,G)由 $s^{ }.一世n吨H和一世n吨r○d你C吨○r和s和C吨一世○n,在和pr和s和n吨一种s你一世吨一种b一世和和X一种米p一世和.吨H和r和,吨H和米和CH一种n一世s米(吨,F一世rs吨−pr一世C和一种你C吨一世○n)一世s你s和d吨○d和r一世v和吨H和米和CH一种n一世s米(吨,H一种一世F−pr一世C和一种你C吨一世○n)b和吨H和H一种一世F−b一世ds吨r一种吨和G和C○米b一世n一种吨一世○ns^{ }.F一世G你r和X五一世一世一世.2d和p一世C吨s\zeta ^ {s ^ { }}一种s吨H和C○米p○s一世吨一世○n\ zeta \ circ s ^ { }○FF你nC吨一世○ns\zeta一种nds^{*}$ 其中
- 首先,$s^{ }一世s一种pp一世一世和d吨○一种吨和p和C○米b一世n一种吨一世○nt \in T吨○和一世和一世d吨H和米和ss一种G和C○米b一世n一种吨一世○ns^{ }(t) \in M$ 和
- 第二,G应用于该消息组合,以便我们获得结果G(s∗(吨))∈和.
我们现在转向著名的启示原则。我们通过占优策略(定理 XVIII.1)和贝叶斯均衡(定理 XVIII.2)给出了实现的证明。

matlab代写请认准UprivateTA™.
经济代写
计量经济学代写请认准my-assignmentexpert™ Economics 经济学作业代写
微观经济学代写请认准my-assignmentexpert™ Economics 经济学作业代写
宏观经济学代写请认准my-assignmentexpert™ Economics 经济学作业代写