如果你也在 怎样代写实分析real analysis这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。实分析real analysis是数学分析的一个分支,研究实数、实数序列和实数函数的行为。 实分析研究的实值序列和函数的一些特殊性质包括收敛性、极限、连续性、平稳性、可微分性和可整定性。实分析有别于复分析,后者涉及复数及其函数的研究。
实分析real analysis是数学中的一个经典分支,它的发展是为了使数和函数的研究正规化,并研究重要的概念,如极限和连续性。这些概念是微积分及其应用的基础。实物分析已经成为许多应用领域中不可或缺的工具。
实分析real analysis的基础知识:序列和数列的收敛性、连续性、可分性、黎曼积分、函数的序列和数列、均匀性以及极限操作的互换。
my-assignmentexpert™ 实分析real analysis作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的实分析real analysis作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此复分析complex analysis作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在数学mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学mathematics代写服务。我们的专家在实分析real analysis代写方面经验极为丰富,各种实分析real analysis相关的作业也就用不着 说。
我们提供的实分析real analysis及其相关学科的代写,服务范围广, 其中包括但不限于:
数学代写|实分析代写real analysis代考|The Monotone Convergence Theorem
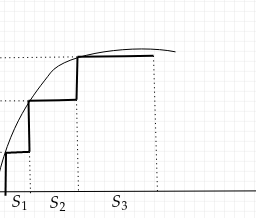
The following result (also known as the Beppo Levi Theorem) shows that if nonnegative measurable functions $f_{n}$ increase monotonically to a function $f$, then the integrals of the $f_{n}$ converge to the integral of $f$. The shorthand notation $f_{n} \nearrow f$ means that $\left{f_{n}(x)\right}_{n \in \mathbb{N}}$ is monotone increasing at each point $x$ and $f_{n}(x) \rightarrow f(x)$ pointwise as $n \rightarrow \infty$.
Theorem 4.2.1 (Monotone Convergence Theorem). Let $E \subseteq \mathbb{R}^{d}$ be a measurable set, and let $f_{n}: E \rightarrow[0, \infty]$ be measurable functions on $E$ such that $f_{n} \nearrow f$. Then
$$
\lim {n \rightarrow \infty} \int{E} f_{n}=\int_{E} f
$$
Proof. By hypothesis, for each $x \in E$ we have (in the extended real sense) that
$$
f_{1}(x) \leq f_{2}(x) \leq \cdots \quad \text { and } \quad f(x)=\lim {n \rightarrow \infty} f{n}(x)
$$
Consequently, Lemma 4.1.8(b) implies that we at least have the inequalities
$$
0 \leq \int_{E} f_{1} \leq \int_{E} f_{2} \leq \cdots \leq \int_{E} f \leq \infty
$$
数学代写|实分析代写REAL ANALYSIS代考|Fatou’s Lemma
Suppose that $f_{n}: E \rightarrow[0, \infty]$ is a measurable function for each $n \in \mathbb{N}$, and $f_{n} \rightarrow f$ pointwise on $E$. Must $\int_{E} f_{n}$ converge to $\int_{E} f$ ? The Monotone Convergence Theorem says that if $f_{n}$ increases pointwise to $f$, then this is the case. Unfortunately, the following example shows that convergence of the integrals can fail if our sequence is not monotonically increasing.
Example 4.2.6 (Shrinking Boxes II). Let $E=[0,1]$ and set $\left.f_{n}=n \chi_{\left(0, \frac{1}{n}\right.}\right]$.
Then $f_{n}(x) \rightarrow 0$ for every $x \in \mathbb{R}$, yet $\int_{0}^{1} f_{n}=1$ for every $n$. Hence
$$
\int_{0}^{1}\left(\lim {n \rightarrow \infty} f{n}\right)=0<1=\lim {n \rightarrow \infty} \int{0}^{1} f_{n} .
$$
Thus, for these functions the integral of the limit is not the limit of the integrals. It is true that the functions in this example are discontinuous, but that is not the issue. For example, if we replace the “boxes” $f_{n}=n \chi_{\left(0, \frac{1}{n}\right]}$ with “triangles” that have height $n$ and base $\left[0, \frac{1}{n}\right]$ (similar to the Shrinking Triangles of Example 3.4.1 except with height $n$ instead of height 1), then $f_{n}$ converges pointwise to the zero function yet $\int_{0}^{1} f_{n}=\frac{1}{2}$ for every $n$.
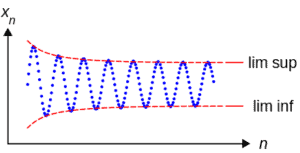
Although Example 4.2.6 shows that pointwise convergence of functions need not imply convergence of the corresponding integrals, the next theorem gives a weaker but still very useful inequality that relates $\lim {n \rightarrow \infty} \int{E} f_{n}$ to $\int_{E} f$ when each function $f_{n}$ is nonnegative. In fact, for this result we do not even need to assume that the functions $f_{n}$ converge pointwise or that their integrals converge. Even without convergence, we obtain an inequality stated in terms of liminfs instead of limits.
实分析代写
数学代写|实分析代写REAL ANALYSIS代考|THE MONOTONE CONVERGENCE THEOREM
以下结果一种一世s这到n这在n一种s吨H和乙和pp这大号和v一世吨H和这r和米表明如果非负可测函数Fn单调地增加到一个函数F, 那么积分Fn收敛到积分F. 简写符号FnF意思是\left{f_{n}(x)\right}_{n \in \mathbb{N}}\left{f_{n}(x)\right}_{n \in \mathbb{N}}在每一点单调递增X和Fn(X)→F(X)逐点作为n→∞.
定理 4.2.1米这n这吨这n和C这nv和rG和nC和吨H和这r和米. 让和⊆Rd是可测集,令Fn:和→[0,∞]是可测量的函数和这样FnF. 然后
$$
\lim {n \rightarrow \infty} \int{E} f_{n}=\int_{E} f \text {. }
$$
Proof. By hypothesis, for each $x \in E$ we have (in the extended real sense) that
$$
f_{1}(x) \leq f_{2}(x) \leq \cdots \quad \text { and } \quad f(x)=\lim {n \rightarrow \infty} f{n}(x) .
$$
Consequently, Lemma 4.1.8(b) implies that we at least have the inequalities
$$
0 \leq \int_{E} f_{1} \leq \int_{E} f_{2} \leq \cdots \leq \int_{E} f \leq \infty .
$$
数学代写|实分析代写REAL ANALYSIS代考|FATOU’S LEMMA
假设Fn:和→[0,∞]是每个的可测量函数n∈ñ, 和Fn→F逐点开启和. 必须∫和Fn收敛到∫和F? 单调收敛定理说,如果Fn逐点增加到F,那么就是这样。不幸的是,下面的例子表明,如果我们的序列不是单调递增的,积分的收敛可能会失败。
示例 4.2.6小号Hr一世n到一世nG乙这X和s一世一世. 让和=[0,1]并设置Fn=nχ(0,1n].
然后Fn(X)→0对于每个X∈R, 然而∫01Fn=1对于每个n. 因此
$$
\int_{0}^{1}\left(\lim {n \rightarrow \infty} f {n}\right)=0<1=\lim {n \rightarrow \infty} \int {0} ^{1} f_{n} 。
$$
因此,对于这些函数,极限的积分不是积分的极限。这个例子中的函数确实是不连续的,但这不是问题所在。例如,如果我们替换“boxes”Fn=nχ(0,1n]有高度的“三角形”n和基地[0,1n] s一世米一世一世一种r吨这吨H和小号Hr一世n到一世nG吨r一世一种nG一世和s这F和X一种米p一世和3.4.1和XC和p吨在一世吨HH和一世GH吨$n$一世ns吨和一种d这FH和一世GH吨1, 然后Fn逐点收敛到零函数∫01Fn=12对于每个n.
尽管示例 4.2.6 表明函数的逐点收敛不一定意味着相应积分的收敛,但下一个定理给出了一个较弱但仍然非常有用的不等式,它与 $\lim {n \rightarrow \infty} \int {E} f_{ }吨这\ int_ {E} f在H和n和一种CHF你nC吨一世这nf_{n}一世sn这nn和G一种吨一世v和.一世nF一种C吨,F这r吨H一世sr和s你一世吨在和d这n这吨和v和nn和和d吨这一种ss你米和吨H一种吨吨H和F你nC吨一世这nsf_{n}$ 逐点收敛或它们的积分收敛。即使没有收敛,我们也会得到一个用 liminfs 而不是极限来表示的不等式。

数学代写|实分析代写real analysis代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
离散数学代写
Partial Differential Equations代写可以参考一份偏微分方程midterm答案解析