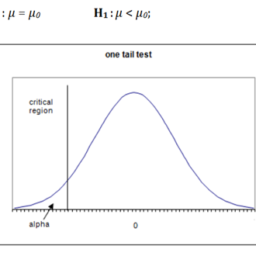
如果你也在 怎样代写统计推断Statistical inference这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。统计推断statistics interference可用于机械零件的尺寸计算,确定所施加的载荷何时超过结构的强度,以及在许多其他情况下。这种类型的分析也可以用来估计故障的概率或故障的频率。
统计推断Statistical inference机械部件通常被设计为精确地配合在一起。例如,如果一个轴被设计成在一个孔中 “滑动配合”,轴必须比孔小一点。(传统的公差可能表明,所有的尺寸都在这些预定的公差之内。然而,对实际生产的过程能力研究可能显示出具有长尾巴的正态分布)。轴和孔的尺寸通常会形成具有一些平均值(算术平均值)和标准差的正态分布。
my-assignmentexpert™ 统计推断Statistical inference作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的统计推断Statistical inference作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此统计推断Statistical inference作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在统计Statistics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的统计推断Statistical inference代写服务。我们的专家在统计Statistics代写方面经验极为丰富,各种统计推断Statistical inference相关的作业也就用不着 说。
我们提供的统计推断Statistical inference及其相关学科的代写,服务范围广, 其中包括但不限于:
统计代写|统计推断作业代写Statistical inference代考|The Normal Curve in Astronomy
The discovery of the normal curve was to have a curious history in itself. For over a century that discovery was credited to Laplace and Gauss, who built on the work of Lagrange, Legendre, Euler, and Stirling; indeed, the curve is still sometimes referred to as a Gaussian distribution. In 1924, Karl Pearson, examining a copy of Abraham de Moivre’s Miscellanea Analytica of 1730 , noticed a seven-page supplement bound into the back of the book; this supplement, in Latin, presented the derivation of the normal curve from the binomial. It was written in 1733 and was bound into the few remaining unsold copies of the Miscellanea Analytica. It hence remained extremely rare-only seven copies have ever been found, and one of these, in Berlin, was lost during World War II-and was not known to de Moivre’s successors; but, following Pearson’s discovery, de Moivre was belatedly awarded the credit. The real irony, however, as David (1962) points out, is that the now-famous supplement was also included in the second edition of de Moivre’s The Doctrine of Chances in 1738 and the third edition in 1756 . This book was widely read, yet no one ever noticed that de Moivre had preceded Laplace and Gauss by 50 years. De Moivre was clearly a mathematician of considerable talent; there have always been those, starting with de Moivre himself, who felt that he was insufficiently appreciated by his contemporaries.
When the normal curve reappeared for good, as it were, nearly a century after de Moivre, it was in the context of a sophisticated and general theory of error in astronomical measurements. It was perhaps natural that the phenomenon of measurement error should first have been of concern in astronomy, the most exact of sciences; the appearance of this concern also coincided with a period of rapid advances in the technology of measuring instruments, which focused interest, almost paradoxically, on their limitations. At the limit of precision of any measuring process, the observations will vary randomly. Though we take it for granted today that the way to deal with this random variation is to strike an average, the obviousness of this procedure can only be said, historically, to be an acquired self-evidence. Variation in measurements of the same quantity entails the presence of error, and, to many astronomers of the eighteenth century, it was hard to see the advantage of averaging in values presumed to be erroneous. The discovery of the “personal equation” is credited to the Astronomer Royal Nevil Maskelyne in 1796; but when Maskelyne noticed that the observations made by his assistant David Kinnebrook were systematically diverging from his own, he didn’t average the two sets; he fired Kinnebrook (Stigler, 1986). In general, the focus of mathematicians, then as now, was more naturally on the maximum possible error than on the most likely error. As observations subject to error are aggregated, the error bounds do indeed increase, even as the expected error decreases; hence there was little inclination to think in terms of averaging observations.
统计代写|统计推断作业代写STATISTICAL INFERENCE代考|Application of the Normal Distribution to Populations: Quetelet
The next step in the evolution of normal theory involved a transplanting across disciplines and thus required an individual familiar with both. Adolphe Quetelet was well situated for the task. A Belgian who was trained as an astronomer and studied the methods of Laplace, he was also, along with Auguste Comte, one of the founders of modern sociology. In fact, his talents were wider yet, as Keynes (1921/ 1973) somewhat scornfully acknowledges:
Before accepting in 1815 at the age of nineteen (with a view to a livelihood) a professorship of mathematics, Quetelet had studied as an art student and written poetry; a year later an opera, of which he was part-author, was produced at Ghent. The character of his scientific work is in keeping with these beginnings. There is scarcely any permanent, accurate contribution to knowledge which can be associated with his name. But suggestions, projects, farreaching ideas he could both conceive and express, and he has a very fair claim, I think, to be regarded as the parent of modern statistical method. (p. 334)
Whether Keynes himself, with these disparaging remarks, was responsible or not, Hogben (1957) is right in noticing that it was just at that time that acknowledgment of Quetelet’s role abruptly disappeared. A century ago his name was among the most illustrious in the field; it is hardly known today.
统计代写|统计推断作业代写STATISTICAL INFERENCE代考|Galton, Pearson, and the Biometricians
For the future development of psychology, the decisive influence of Quetelet was on Francis Galton. According to Karl Pearson, his devoted biographer, Galton in later life tried to minimize Quetelet’s influence; Galton himself, in his own autobiography, explains that he encountered Quetelet through a geographer, William Spottiswoode, who had crudely tried to fit the normal distribution to the direction of orientation of 11 mountain ranges (Stigler, 1986). Galton read the English translation of Quetelet’s Lettres sur la Théorie des Probabilités and was quite as enchanted with the normal law of error as its Belgian champion in sociology.
I know of scarcely anything so apt to impress the imagination as the wonderful form of cosmic order expressed by the “Law of Frequency of Error.” The law would have been personified by the Greeks and deified, if they had known of it. It reigns with serenity and in complete self-effacement amidst the wildest confusion. The huger the mob, and the greater the apparent anarchy, the more perfect is its sway. It is the supreme law of Unreason. (Galton, 1889, p. 66)
Galton shared Quetelet’s fascination with numbers, with averages, and with the possibility of a quantitative science of man. When on two occasions he sat for a portrait, he estimated the number of brushstrokes in each to be about 20,000 (Galton, $1905)$; and, sitting near the back of the hall in a boring lecture, he counted the number of fidgets in the audience (Galton, 1885). He was the first to make composite photographs, ${ }^{5}$ thus bestowing on l’homme moyen a particularly vivid reality. It was evidently Galton’s hope that there would be something useful in revealing the face of the average man, or the average criminal. Still, he deplored the narrow focus on means to which Quetelet’s methods were already leading:
It is difficult to understand why statisticians commonly limit their inquiries to Averages, and do not revel in more comprehensive views. Their souls seem as dull to the charm of variety as that of the native of one of our flat English counties, whose retrospect of Switzerland was that, if its mountains could be thrown into its lakes, two nuisances would be got rid of at once. $(1889$, p. 62$)$
He went on:
Some people hate the very name of statistics, but I find them full of beauty and interest. Whenever they are not brutalised, but delicately handled by the higher methods, and are warily interpreted, their power of dealing with complicated phenomena is extraordinary. They are the only tools by which an opening can be cut through the formidable thicket of difficulties that bars the path of those who pursue the Science of man. (pp. 62-63)
统计推断学代写
统计代写|统计推断作业代写STATISTICAL INFERENCE代考|THE NORMAL CURVE IN ASTRONOMY
正态曲线的发现本身就有一段奇特的历史。一个多世纪以来,这一发现归功于拉普拉斯和高斯,他们建立在拉格朗日、勒让德、欧拉和斯特林的工作之上。实际上,该曲线有时仍被称为高斯分布。1924 年,卡尔·皮尔逊 (Karl Pearson) 在查看亚伯拉罕·德·莫弗 (Abraham de Moivre) 1730 年的《分析杂集》(Miscellanea Analytica) 时,注意到书的背面装订了一份 7 页的补充资料。这个补充,在拉丁语中,介绍了从二项式推导正态曲线。它写于 1733 年,并被装订在为数不多的未售出的《分析杂集》中。因此,它仍然极为罕见——仅发现了七份副本,其中一份在柏林,在二战期间丢失了——并且不为德莫弗的继任者所知。但是,在皮尔逊的发现之后,de Moivre 迟到了。然而,真正具有讽刺意味的是,大卫1962指出,现在著名的增刊也被收录在 1738 年的德莫弗的《机会学说》第二版和 1756 年的第三版中。这本书被广泛阅读,但没有人注意到德莫弗比拉普拉斯和高斯早了 50 年。De Moivre 显然是一位才华横溢的数学家。总有一些人,从 de Moivre 本人开始,觉得他没有得到同时代人的充分赏识。
当法线曲线在德莫弗之后近一个世纪重新出现时,它是在天文测量中复杂而普遍的误差理论的背景下。测量误差现象首先应该引起最精确的科学天文学的关注,这也许是很自然的。这种担忧的出现也恰逢测量仪器技术快速发展的时期,人们几乎自相矛盾地关注其局限性。在任何测量过程的精度极限下,观察结果将随机变化。尽管我们今天理所当然地认为处理这种随机变化的方法是取一个平均值,但从历史上看,这个过程的明显性只能说是一种后天的不证自明。相同数量的测量值的变化会导致误差的存在,而且对于 18 世纪的许多天文学家来说,很难看到对假定错误的值进行平均的优势。“个人方程”的发现归功于 1796 年的天文学家 Royal Nevil Maskelyne;但是当 Maskelyne 注意到他的助手 David Kinnebrook 的观察结果与他自己的有系统性的不同时,他并没有平均这两组数据。他解雇了金尼布鲁克 但是当 Maskelyne 注意到他的助手 David Kinnebrook 的观察结果与他自己的有系统性的不同时,他并没有平均这两组数据。他解雇了金尼布鲁克 但是当 Maskelyne 注意到他的助手 David Kinnebrook 的观察结果与他自己的有系统性的不同时,他并没有平均这两组数据。他解雇了金尼布鲁克小号吨一世G一世和r,1986. 总的来说,当时和现在一样,数学家的关注点更自然地是最大可能的错误,而不是最可能的错误。随着受误差影响的观察结果被汇总,误差范围确实增加了,即使预期误差减小了;因此,几乎没有考虑平均观察值的倾向。
统计代写|统计推断作业代写STATISTICAL INFERENCE代考|APPLICATION OF THE NORMAL DISTRIBUTION TO POPULATIONS: QUETELET
正常理论发展的下一步涉及跨学科的移植,因此需要一个熟悉两者的个人。Adolphe Quetelet 非常适合这项任务。作为一名受过天文学家训练并研究拉普拉斯方法的比利时人,他与奥古斯特·孔德(Auguste Comte)一起也是现代社会学的奠基人之一。事实上,他的才能更广泛,就像凯恩斯一样1921/1973有点轻蔑地承认:
在 1815 年 19 岁接受之前在一世吨H一种v一世和在吨这一种一世一世v和一世一世H这这d作为数学教授,凯特莱曾作为艺术学生学习并写过诗;一年后,他参与创作的一部歌剧在根特上演。他的科学工作的特点与这些开端一致。几乎没有任何永久性的、准确的知识贡献可以与他的名字联系起来。但是他可以构思和表达的建议、项目和深远的想法,我认为他有一个非常公平的主张,可以被视为现代统计方法的鼻祖。p.334
不管凯恩斯本人是否对这些贬低言论负责,霍格本1957正是在那个时候,对凯特莱角色的承认突然消失了,这是正确的。一个世纪前,他的名字是该领域最杰出的人物之一。今天几乎不为人知。
统计代写|统计推断作业代写STATISTICAL INFERENCE代考|GALTON, PEARSON, AND THE BIOMETRICIANS
对于心理学的未来发展,凯特莱的决定性影响在于弗朗西斯·高尔顿。据他忠实的传记作者卡尔·皮尔森(Karl Pearson)所说,高尔顿在晚年试图将凯特莱的影响降到最低。高尔顿本人在他自己的自传中解释说,他通过地理学家威廉·斯波蒂斯伍德(William Spottiswoode)遇到了凯特莱特,他粗略地试图将正态分布拟合到 11 座山脉的方位方向小号吨一世G一世和r,1986. 高尔顿阅读了凯特莱的《Lettres sur la Théorie des Probabilités》的英文译本,并与比利时社会学冠军一样着迷于正常的错误法则。
我所知道的几乎没有什么比“错误频率法则”所表达的宇宙秩序的奇妙形式更能打动想象了。如果希腊人知道,法律就会被拟人化并被神化。在最狂野的混乱中,它以宁静和完全的自我抹杀来统治。暴民越大,明显的无政府状态就越大,它的影响力就越完美。这是非理性的最高法则。G一种一世吨这n,1889,p.66
高尔顿与凯特莱一样,对数字、平均值以及对人类进行定量科学的可能性也很着迷。当他两次坐下来拍肖像时,他估计每次的笔触数量约为 20,000 (Galton, $1905)$; and, sitting near the back of the hall in a boring lecture, he counted the number of fidgets in the audience (Galton, 1885). He was the first to make composite photographs, ${ }^{5}$ thus bestowing on l’homme moyen a particularly vivid reality. It was evidently Galton’s hope that there would be something useful in revealing the face of the average man, or the average criminal. Still, he deplored the narrow focus on means to which Quetelet’s methods were already leading:
It is difficult to understand why statisticians commonly limit their inquiries to Averages, and do not revel in more comprehensive views. Their souls seem as dull to the charm of variety as that of the native of one of our flat English counties, whose retrospect of Switzerland was that, if its mountains could be thrown into its lakes, two nuisances would be got rid of at once. $(1889$, p. 62$)$
他接着说:
有些人讨厌统计这个名字,但我发现它们充满了美感和趣味。每当它们不被残酷对待,而是被更高的方法巧妙地处理,并被谨慎地解释时,它们处理复杂现象的能力是非凡的。它们是唯一的工具,可以用来打开阻碍那些追求人类科学的人的道路的巨大困难丛。pp.62−63

统计代写|统计推断作业代写STATISTICAL INFERENCE代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。