如果你也在 怎样代写偏微分方程Partial Differential Equations这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。偏微分方程Partial Differential Equations是一个方程,它规定了一个多变量函数的各种偏导数之间的关系。该函数通常被认为是一个有待解决的 “未知数”,类似于x被认为是代数方程(如x2-3x+2=0)中有待解决的一个未知数。因此,在现代数学和科学研究中,有大量使用计算机对某些偏微分方程的解进行数值近似的方法。
偏微分方程Partial Differential Equations在以数学为导向的科学领域,如物理学和工程学中无处不在。例如,它们是现代科学对声音、热量、扩散、静电、电动力学、热力学、流体动力学、弹性、广义相对论和量子力学(薛定谔方程、保利方程等)的基础性认识。它们也产生于许多纯粹的数学考虑,如微分几何和变分计算;在其他值得注意的应用中,它们是几何拓扑学中证明庞加莱猜想的基本工具。
my-assignmentexpert™ 偏微分方程Partial Differential Equations作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的偏微分方程Partial Differential Equations作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此偏微分方程Partial Differential Equations作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的偏微分方程Partial Differential Equations代写服务。我们的专家在数学Mathematics代写方面经验极为丰富,各种偏微分方程Partial Differential Equations相关的作业也就用不着 说。
我们提供的偏微分方程Partial Differential Equations及其相关学科的代写,服务范围广, 其中包括但不限于:
调和函数 harmonic function
椭圆方程 elliptic equation
抛物方程 Parabolic equation
双曲方程 Hyperbolic equation
非线性方法 nonlinear method
变分法 Calculus of Variations
几何分析 geometric analysis
偏微分方程数值解 Numerical solution of partial differential equations
数学代写|偏微分方程作业代写Partial Differential Equations代考|The Domain of Dependence and Influence
The most general way to view causality (what causes what) is via the domain of dependence and domain of influence. Both are regions in the $x$ – vs. $t$-plane (space-time), one based upon the past and the other on the future.
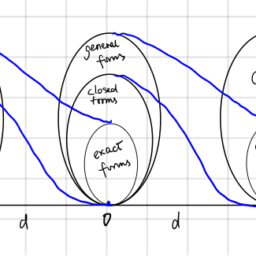
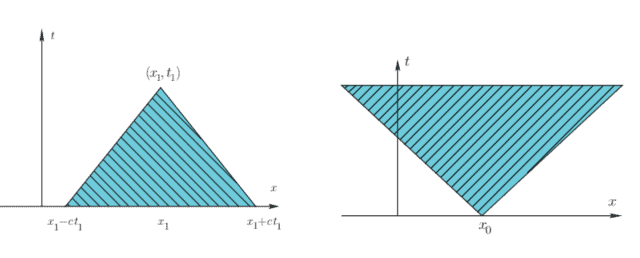
The first is the domain of dependence, illustrated in Figure 3.3: Here we fix a point $\left(x_{1}, t_{1}\right)$ in space-time and look at the past. To this end, consider the dependence of the solution $u\left(x_{1}, t_{1}\right)$ on the initial data. Using D’Alembert’s formula, the solution $u\left(x_{1}, t_{1}\right)$ depends on the initial displacements at positions $x_{1}-c t_{1}$ and $x_{1}+c t_{1}$ and all the initial velocities between them. Hence, it depends on what happened initially (displacement and velocity) in the interval $\left[x_{1}-c t_{1}, x_{1}+c t_{1}\right]$. Now let us consider any earlier time $t_{2}$, i.e., $0<t_{2}<t_{1}$, starting our stopwatch here. We can think of $t_{2}$ as the initial time and ask what positions are relevant at time $t_{2}$ for determining $u\left(x_{1}, t_{1}\right)$. This is a shorter interval as less time has elapsed from $t_{2}$ to $t_{1}$ than from 0 to $t_{1}$. In fact the interval is exactly $\left[x_{1}-c\left(t_{1}-t_{2}\right), x_{1}+c\left(t_{1}-t_{2}\right)\right]$. Thus, the entire domain of dependence for a point $\left(x_{1}, t_{1}\right)$ in space-time is the shaded triangular region shown on the left of Figure 3.3.
数学代写|偏微分方程作业代写Partial Differential Equations代考|Two Examples: A Plucked String and a Hammer Blow
We present two examples wherein one of the data functions is identically 0 . They correspond, respectively, to the situations of a plucked string and a hammer blow.
Warning: In each case, the illustrated dynamics given by the wave equation will not coincide with your intuition of plucking a guitar string nor hitting a piano string. This is because of our assumption of an infinitely long string. An actual guitar, or piano, string is finite with fixed ends (no displacement at the end points), and as we shall see later, these boundary conditions greatly affect the wave dynamics.
The Plucked String. Let $c=1$,
$$
\phi(x)= \begin{cases}1-|x,| & |x| \leq 1 \ 0, & |x|>1\end{cases}
$$
and $\psi \equiv 0$. By D’Alembert’s formula, the solution is
$$
u(x, t)=\frac{1}{2}[\phi(x+t)+\phi(x-t)] .
$$
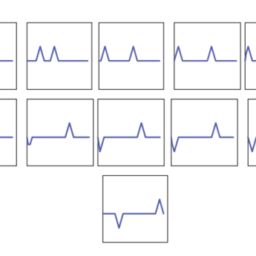
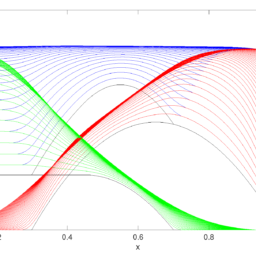
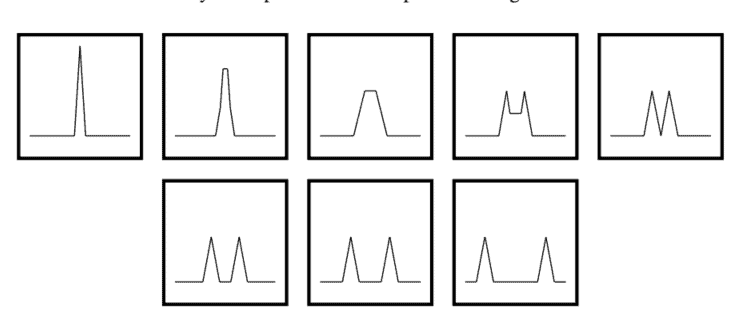
Thus, at any time $t$, the solution is simply the sum of two waves with the same initial shape but half the amplitude, one which has moved to the right by $t$ and one which has moved to the left by $t$. We plot some of the profiles in Figure 3.4.
偏微分方程代写
数学代写|偏微分方程作业代写PARTIAL DIFFERENTIAL EQUATIONS代考|THE DOMAIN OF DEPENDENCE AND INFLUENCE
查看因果关系的最一般方法在H一种吨C一种在s和s在H一种吨是通过依赖域和影响域。两者都是地区X- 与。吨-飞机sp一种C和−吨一世米和,一个基于过去,另一个基于未来。
第一个是依赖域,如图 3.3 所示:这里我们固定一个点(X1,吨1)在时空中看过去。为此,考虑解决方案的依赖性在(X1,吨1)关于初始数据。使用 D’Alembert 公式,解在(X1,吨1)取决于位置处的初始位移X1−C吨1和X1+C吨1以及它们之间的所有初始速度。因此,这取决于最初发生的事情d一世spl一种C和米和n吨一种nd在和l这C一世吨是在区间[X1−C吨1,X1+C吨1]. 现在让我们考虑任何更早的时间吨2, IE,0<吨2<吨1,在这里开始我们的秒表。我们可以想到吨2作为初始时间,并询问当时哪些职位是相关的吨2用于确定在(X1,吨1). 这是一个较短的间隔,因为从吨2到吨1比从 0 到吨1. 实际上间隔正好[X1−C(吨1−吨2),X1+C(吨1−吨2)]. 因此,一个点的整个依赖域(X1,吨1)在时空中是图 3.3 左侧所示的阴影三角形区域。
数学代写|偏微分方程作业代写PARTIAL DIFFERENTIAL EQUATIONS代考|TWO EXAMPLES: A PLUCKED STRING AND A HAMMER BLOW
我们提出两个示例,其中数据函数之一是相同的 0 。它们分别对应于拨弦和锤击的情况。
警告:在每种情况下,波动方程给出的图示动力学与您弹奏吉他弦或弹奏钢琴弦的直觉不一致。这是因为我们假设一个无限长的字符串。真正的吉他或钢琴弦是有固定末端的n这d一世spl一种C和米和n吨一种吨吨H和和ndp这一世n吨s,正如我们稍后将看到的,这些边界条件极大地影响了波浪动力学。
弹拨弦。让C=1,
φ(X)={1−|X,||X|≤1 0,|X|>1
和ψ≡0. 根据 D’Alembert 公式,解为
在(X,吨)=12[φ(X+吨)+φ(X−吨)].
因此,任何时候吨,解决方案只是两个具有相同初始形状但幅度为一半的波的总和,其中一个波向右移动了吨一个已经向左移动了吨. 我们在图 3.4 中绘制了一些配置文件。

数学代写|偏微分方程作业代写Partial Differential Equations代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。