如果你也在 怎样代写偏微分方程Partial Differential Equations这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。偏微分方程Partial Differential Equations是一个方程,它规定了一个多变量函数的各种偏导数之间的关系。该函数通常被认为是一个有待解决的 “未知数”,类似于x被认为是代数方程(如x2-3x+2=0)中有待解决的一个未知数。因此,在现代数学和科学研究中,有大量使用计算机对某些偏微分方程的解进行数值近似的方法。
偏微分方程Partial Differential Equations在以数学为导向的科学领域,如物理学和工程学中无处不在。例如,它们是现代科学对声音、热量、扩散、静电、电动力学、热力学、流体动力学、弹性、广义相对论和量子力学(薛定谔方程、保利方程等)的基础性认识。它们也产生于许多纯粹的数学考虑,如微分几何和变分计算;在其他值得注意的应用中,它们是几何拓扑学中证明庞加莱猜想的基本工具。
my-assignmentexpert™ 偏微分方程Partial Differential Equations作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的偏微分方程Partial Differential Equations作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此偏微分方程Partial Differential Equations作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的偏微分方程Partial Differential Equations代写服务。我们的专家在数学Mathematics代写方面经验极为丰富,各种偏微分方程Partial Differential Equations相关的作业也就用不着 说。
我们提供的偏微分方程Partial Differential Equations及其相关学科的代写,服务范围广, 其中包括但不限于:
调和函数 harmonic function
椭圆方程 elliptic equation
抛物方程 Parabolic equation
双曲方程 Hyperbolic equation
非线性方法 nonlinear method
变分法 Calculus of Variations
几何分析 geometric analysis
偏微分方程数值解 Numerical solution of partial differential equations
数学代写|偏微分方程作业代写Partial Differential Equations代考|A Few Examples
Example 2.2.1. Recall the example
$$
\left{\begin{array}{l}
a u_{x}+b u_{y}=0, \
u(x, 0)=x^{3},
\end{array}\right.
$$
where $a, b$ are fixed real numbers. We have done this one before but let us redo it using the method of characteristics. The characteristic system of ODEs is
$$
\dot{x}(s)=a, \quad \dot{y}(s)=b, \quad \dot{z}(s)=0 .
$$
Solving the $x$ and $y$ equations first gives
$$
x(s)=a s+c_{1}, \quad y(s)=b s+c_{2} .
$$
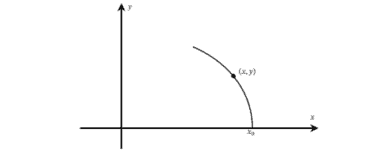
What do we take for the “constants” $c_{1}$ and $c_{2}$ ? In other words, how do we choose the initial conditions for the ODEs? We choose them so that at $s=0,(x(0), y(0))$ corresponds to a point on the data curve, here the $x$-axis. Thus we take $c_{2}=0$. The value of $c_{1}$ will then correspond to the intersection point on the $x$-axis. It will index the different lines (characteristics). Let us also use more descriptive notation for $c_{1}$ and denote it by $x_{0}$ since it corresponds to the point of intersection between the characteristic and the $x$-axis. Equivalently, we are solving the ODEs with initial values $(x(0), y(0))=\left(x_{0}, 0\right)$.
Now the solution to the $z$ equation is simply
$$
z=c_{3} \text {, }
$$
but since $z(0)$ corresponds to $u(x(0), y(0))=u\left(x_{0}, 0\right)=x_{0}^{3}$, we must have $c_{3}=x_{0}^{3}$. Thus
$$
x(s)=a s+x_{0}, \quad y(s)=b s, \quad z=z_{0}=x_{0}^{3} .
$$
OK, what do we have so far? We have equations for the characteristic curves $(x(s), y(s))$ which lie in the domain of the unknown solution. These curves are indexed (labeled) by $x_{0}$, the $x$ coordinate of their intersection with the $x$-axis. We also know the value of the solution $u$ along any one of these curves. This value is different on each curve and hence the appearance of $x_{0}$ in the equation for $z$. Surely, we can piece this all together to find a formula for $u(x, y)$ in terms of $x$ and $y$ (no $x_{0}$ or $s$ in the formula!). Indeed, given $(x, y)$, we need to know
- what characteristic this point lies on (i.e., which $x_{0}$ ) and
- where along this characteristic the point lies (i.e., the value of $s$ ).
数学代写|偏微分方程作业代写Partial Differential Equations代考|Temporal Equations: Using Time to Parametrize the Character
istics. In many cases, time is one of the independent variables and we are given the values of the solution at $t=0$. In these cases, the linear PDE for $u(x, t)$ can always be written in a form where the coefficient of $u_{t}$ is 1 ; otherwise, we can divide through the original equation by the coefficient of $u_{t}$. In fact, most of the time the PDE will be presented in the form
$$
u_{t}+\cdots=0
$$
Since the data will be given on the $t=0$ axis, the characteristic ODE for $t$,
$$
\dot{t}(s)=1,
$$
will be solved with condition $t(0)=0$. Thus we have
$$
t(s)=s \quad \text { or } \quad t=s,
$$
and we may as well use $t$ (time) as the parameter of our characteristics, eliminating the variable $s$. In this case, the characteristics $(x(s), t(s))=(x(t), t)$ in the $x$-vs. $t$-plane can be written with the scalar equation for $x=x(t)$. We give an example.
数学代写|偏微分方程作业代写PARTIAL DIFFERENTIAL EQUATIONS代考|More Than Two Independent Variables
Than Two Independent Variables. Our method can readily be performed when the unknown function depends on more than two variables. A few things change. First, since the domain of our solution $u$ is a subset of $\mathbb{R}^{N}$ with $N \geq 3$, the number of equations for the characteristics will increase. Note that the characteristic will still be curves in $\mathbb{R}^{N}$ – one-dimensional objects. The “one” comes from the order of the PDE. There will, of course, be more than one parameter needed to label these characteristics. In fact, there will be $N-1$ such parameters, and data will now be given on an $(N-1)$-dimensional hypersurface (e.g., a two-dimensional surface for $N=3$ ). These $N-1$ parameters will label all characteristic curves via their intersection with the data hypersurface. The following provides an example with $N=3$.

偏微分方程代写
数学代写|偏微分方程作业代写PARTIAL DIFFERENTIAL EQUATIONS代考|A FEW EXAMPLES
示例 2.2.1。回想一下示例
$$
\left{\begin{array}{l}
a u_{x}+b u_{y}=0, \
u(x, 0)=x^{3},
\end{array}\right.
$$
where $a, b$ are fixed real numbers. We have done this one before but let us redo it using the method of characteristics. The characteristic system of ODEs is
$$
\dot{x}(s)=a, \quad \dot{y}(s)=b, \quad \dot{z}(s)=0 .
$$
Solving the $x$ and $y$ equations first gives
$$
x(s)=a s+c_{1}, \quad y(s)=b s+c_{2} .
$$
What do we take for the “constants” $c_{1}$ and $c_{2}$ ? In other words, how do we choose the initial conditions for the ODEs? We choose them so that at $s=0,(x(0), y(0))$ corresponds to a point on the data curve, here the $x$-axis. Thus we take $c_{2}=0$. The value of $c_{1}$ will then correspond to the intersection point on the $x$-axis. It will index the different lines (characteristics). Let us also use more descriptive notation for $c_{1}$ and denote it by $x_{0}$ since it corresponds to the point of intersection between the characteristic and the $x$-axis. Equivalently, we are solving the ODEs with initial values $(x(0), y(0))=\left(x_{0}, 0\right)$.
Now the solution to the $z$ equation is simply
$$
z=c_{3} \text {, }
$$
but since $z(0)$ corresponds to $u(x(0), y(0))=u\left(x_{0}, 0\right)=x_{0}^{3}$, we must have $c_{3}=x_{0}^{3}$. Thus
$$
x(s)=a s+x_{0}, \quad y(s)=b s, \quad z=z_{0}=x_{0}^{3} .
$$
好的,到目前为止我们有什么?我们有特征曲线的方程(X(s),是(s))它位于未知解决方案的域中。这些曲线被索引l一种b和l和d经过X0, 这X它们的交点坐标X-轴。我们也知道解决方案的价值在沿着这些曲线中的任何一条。该值在每条曲线上都不同,因此X0在等式中和. 当然,我们可以将所有这些拼凑起来找到一个公式在(X,是)按照X和是 n这$X0$这r$s$一世n吨H和F这r米在l一种!. 的确,鉴于(X,是), 我们需要知道
- 这个点有什么特点一世.和.,在H一世CH$X0$和
- 沿着这个特征,重点在哪里一世.和.,吨H和在一种l在和这F$s$.
数学代写|偏微分方程作业代写PARTIAL DIFFERENTIAL EQUATIONS代考|TEMPORAL EQUATIONS: USING TIME TO PARAMETRIZE THE CHARACTER
学问。在许多情况下,时间是自变量之一,我们得到解的值吨=0. 在这些情况下,线性 PDE 为在(X,吨)总是可以写成其中的系数在吨是 1 ; 否则,我们可以通过原始方程除以系数在吨. 事实上,大多数时候 PDE 会以这种形式呈现
在吨+⋯=0
由于数据将在吨=0轴,特征 ODE吨,
吨˙(s)=1,
将有条件解决吨(0)=0. 因此我们有
吨(s)=s 或者 吨=s,
我们也可以使用吨 吨一世米和作为我们特征的参数,消除变量s. 在这种情况下,特征(X(s),吨(s))=(X(吨),吨)在里面X-vs。吨-plane 可以用标量方程写成X=X(吨). 我们举个例子。
数学代写|偏微分方程作业代写PARTIAL DIFFERENTIAL EQUATIONS代考|MORE THAN TWO INDEPENDENT VARIABLES
比两个自变量。当未知函数取决于两个以上的变量时,我们的方法可以很容易地执行。有几件事发生了变化。首先,由于我们解决方案的域在是的一个子集Rñ和ñ≥3,特征方程的数量将增加。请注意,特征仍然是曲线Rñ– 一维对象。“一”来自 PDE 的顺序。当然,标记这些特征需要不止一个参数。其实会有ñ−1这样的参数,和数据现在将给出一个(ñ−1)维超曲面和.G.,一种吨在这−d一世米和ns一世这n一种ls在rF一种C和F这r$ñ=3$. 这些ñ−1参数将通过它们与数据超曲面的交点标记所有特征曲线。下面提供了一个例子ñ=3.

数学代写|偏微分方程作业代写Partial Differential Equations代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。