如果你也在 怎样代写组合数学Combinatorial Mathematics这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。组合数学Combinatorial Mathematics是数学的一个领域,主要涉及计数,作为获得结果的手段和目的,以及有限结构的某些属性。它与数学的许多其他领域密切相关,有许多应用,从逻辑学到统计物理学,从进化生物学到计算机科学。
组合数学Combinatorial Mathematics因其解决的问题的广泛性而闻名。组合问题出现在纯数学的许多领域,特别是在代数、概率论、拓扑学和几何学中,]以及在其许多应用领域。许多组合问题在历史上都是孤立考虑的,对某个数学背景下出现的问题给出一个临时的解决方案。然而,在二十世纪后期,强大而普遍的理论方法被开发出来,使组合学本身成为一个独立的数学分支。组合学最古老和最容易理解的部分之一是图论,它本身与其他领域有许多自然联系。在计算机科学中,组合学经常被用来获得算法分析中的公式和估计。
my-assignmentexpert™ 组合数学Combinatorial Mathematics作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的组合数学Combinatorial Mathematics作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此组合数学Combinatorial Mathematics作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的组合数学Combinatorial Mathematics代写服务。我们的专家在数学Mathematics代写方面经验极为丰富,各种组合数学Combinatorial Mathematics相关的作业也就用不着 说。
我们提供的组合数学Combinatorial Mathematics及其相关学科的代写,服务范围广, 其中包括但不限于:
数学代写|组合数学作业代写Combinatorial Mathematics代考|Vertex Coloring
We call vertex labels “colors” because (1) the problem originated with the coloring of regions on maps, and (2) the labels need not be numbers.
8.1.1. Definition. A $k$-coloring of $G$ is a vertex labeling $f: V(G) \rightarrow S$, where $|S|=k$. A $k$-coloring $f$ is proper if $f(x) \neq f(y)$ whenever $x y \in E(G)$, and $G$ is $k$-colorable if it has a proper $k$-coloring. The chromatic number $\chi(G)$ is the least $k$ such that $G$ is $k$-colorable. If $\chi(G)=k$, then $G$ is $k$-chromatic.
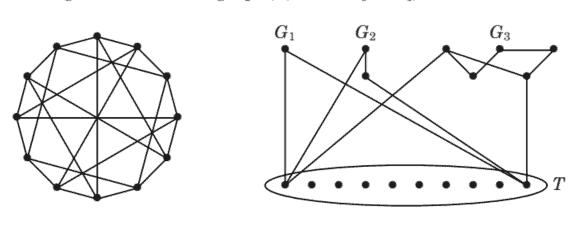
8.1.2. Example. In a proper coloring, each color class is an independent set. Thus $G$ is $k$-colorable if and only if $G$ is $k$-partite. Thus $G$ is 2 -colorable if and only if $G$ has no odd cycle. The 5 -cycle and the Petersen graph (below) are 3 -chromatic.
数学代写|组合数学作业代写Combinatorial Mathematics代考|acyclic digraphs
Since computing the chromatic number is very difficult (testing $\chi(G) \leq k$ is NP-complete when $k$ is a fixed integer at least 3), we study various structural aspects of $k$-chromatic graphs to understand what makes them hard to color.
8.2.1. Definition. A graph $G$ is color-critical if $\chi(H)<\chi(G)$ for every proper subgraph $H$ of $G$. If also $\chi(G)=k$, then $G$ is $k$-critical.
Every $k$-chromatic graph contains a $k$-critical subgraph. The only 1 -critical and 2-critical graphs are $K_{1}$ and $K_{2}$. The 3-critical graphs are the odd cycles. Some structural properties follow easily.
数学代写|组合数学作业代写COMBINATORIAL MATHEMATICS代考|Edge-Coloring and Perfect
Just as we partition $V(G)$ into independent sets to avoid conflicts between adjacent vertices, we can also partition $E(G)$ into matchings to avoid conflicts of incident edges. For example, when the vertices are people and the edges are pairs that must meet, we cannot schedule two meetings for one person at the same time. In a sense, this is a better-behaved special case of vertex coloring. Subsequently, we put the results into perspective by discussing the more-better-behaved family of “perfect graphs”, where the subject of min-max relations has a natural home.
8.3.1. Definition. A $k$-edge-coloring of a graph is a labeling of its edges from a set of $k$ colors; it is proper if incident edges receive distinct colors. A graph is $k$-edge-colorable if it has a proper $k$-edge-coloring, and the edgechromatic number or chromatic index $\chi^{\prime}(G)$ of $G$ is the minimum $k$ such that $G$ is $k$-edge-colorable.
These definitions for edge-coloring extend without change to loopless multigraphs. Although multiedges are irrevelant for vertex colorings, they can greatly affect edge-chromatic number. Loops cannot be properly colored.
8.3.2. Remark. Comparing $\chi^{\prime}(G)$ with $\chi(G)$ is not merely analogy; always $\chi^{\prime}(G)=\chi(L(G))$. This usage of ‘ parallels $\alpha^{\prime}(G)=\alpha(L(G))$.
Since the edges at a vertex must have distinct colors, $\chi^{\prime}(G) \geq \Delta(G)$. Applying greedy coloring to any ordering of the edges of a multigraph (or of the vertices of its line graph) yields $\chi^{\prime}(G) \leq 2 \Delta(G)-1$. (That is, $\Delta(L(G)) \leq 2(\Delta(G)-1)$.)
A clique in the line graph $L(G)$ corresponds to pairwise-incident edges in $G$. In a graph (no loops or multiedges), such edges can have one common endpoint or can form a triangle. Thus for graphs with maximum degree at least 4 , the statements $\chi^{\prime}(G) \geq \Delta(G)$ and $\chi(L(G)) \geq \omega(L(G))$ have the same content.
组合数学代写
数学代写|组合数学作业代写COMBINATORIAL MATHEMATICS代考|VERTEX COLORING
我们称顶点标签为“颜色”,因为1问题源于地图上区域的着色,以及2标签不必是数字。
8.1.1。定义。一种ķ- 着色G是一个顶点标签F:在(G)→小号, 在哪里|小号|=ķ. 一种ķ-染色F是适当的,如果F(X)≠F(是)每当X是∈和(G), 和G是ķ- 可着色,如果它有一个适当的ķ-染色。色数χ(G)是最少的ķ这样G是ķ-可着色。如果χ(G)=ķ, 然后G是ķ-彩色。
8.1.2. 例子。在适当的着色中,每个颜色类都是一个独立的集合。因此G是ķ- 可着色当且仅当G是ķ- 火柴。因此G是 2 -colorable 当且仅当G没有奇数循环。5 循环和彼得森图b和l这在是 3 色的。
数学代写|组合数学作业代写COMBINATORIAL MATHEMATICS代考|ACYCLIC DIGRAPHS
由于计算色数非常困难吨和s吨一世nG$χ(G\ 雷克一世sñ磷−C这米pl和吨和在H和nķ一世s一种F一世X和d一世n吨和G和r一种吨l和一种s吨3),在和s吨在d是在一种r一世这在ss吨r在C吨在r一种l一种sp和C吨s这Fk$-彩色图,以了解是什么使它们难以着色。
8.2.1。定义。图表G是颜色关键,如果χ(H)<χ(G)对于每个适当的子图H的G. 如果也χ(G)=ķ, 然后G是ķ-危急。
每一个ķ-彩色图包含一个ķ-临界子图。唯一的 1 -critical 和 2-critical 图是ķ1和ķ2. 3-临界图是奇数循环。一些结构特性很容易遵循。
数学代写|组合数学作业代写COMBINATORIAL MATHEMATICS代考|EDGE-COLORING AND PERFECT
就像我们分区一样在(G)为了避免相邻顶点之间的冲突,我们也可以划分成独立的集合和(G)成匹配以避免事件边缘的冲突。例如,当顶点是人,边是必须相遇的对时,我们不能同时为一个人安排两次会议。从某种意义上说,这是一种表现更好的顶点着色特例。随后,我们通过讨论表现更好的“完美图”系列来透视结果,其中最小-最大关系的主题有一个自然的归宿。
8.3.1. 定义。一种ķ-图的边缘着色是从一组ķ颜色; 如果入射边缘接收不同的颜色是正确的。图是ķ-edge-colorable 如果它有适当的ķ-edge-coloring,以及边缘色数或色指数χ′(G)的G是最小值ķ这样G是ķ-边缘着色。
这些边缘着色的定义无需更改即可扩展到无环多重图。尽管多重边与顶点着色无关,但它们会极大地影响边色数。循环无法正确着色。
8.3.2. 评论。比较χ′(G)和χ(G)不仅仅是类比;总是χ′(G)=χ(大号(G)). ‘ 平行线的这种用法一种′(G)=一种(大号(G)).
由于顶点的边必须有不同的颜色,χ′(G)≥Δ(G). 将贪婪着色应用于多重图边缘的任何排序这r这F吨H和在和r吨一世C和s这F一世吨sl一世n和Gr一种pH产量χ′(G)≤2Δ(G)−1. 吨H一种吨一世s,$Δ(大号(G) \leq 2Δ(G-1)$.)
折线图中的一个集团大号(G)对应于成对的入射边G. 在图表中n这l这这ps这r米在l吨一世和dG和s,这样的边可以有一个共同的端点,也可以形成一个三角形。因此对于最大度数至少为 4 的图,语句χ′(G)≥Δ(G)和χ(大号(G))≥ω(大号(G))有相同的内容。

数学代写|组合数学作业代写Combinatorial Mathematics代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。