如果你也在 怎样代写组合数学Combinatorial Mathematics这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。组合数学Combinatorial Mathematics是数学的一个领域,主要涉及计数,作为获得结果的手段和目的,以及有限结构的某些属性。它与数学的许多其他领域密切相关,有许多应用,从逻辑学到统计物理学,从进化生物学到计算机科学。
组合数学Combinatorial Mathematics因其解决的问题的广泛性而闻名。组合问题出现在纯数学的许多领域,特别是在代数、概率论、拓扑学和几何学中,]以及在其许多应用领域。许多组合问题在历史上都是孤立考虑的,对某个数学背景下出现的问题给出一个临时的解决方案。然而,在二十世纪后期,强大而普遍的理论方法被开发出来,使组合学本身成为一个独立的数学分支。组合学最古老和最容易理解的部分之一是图论,它本身与其他领域有许多自然联系。在计算机科学中,组合学经常被用来获得算法分析中的公式和估计。
my-assignmentexpert™ 组合数学Combinatorial Mathematics作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的组合数学Combinatorial Mathematics作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此组合数学Combinatorial Mathematics作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的组合数学Combinatorial Mathematics代写服务。我们的专家在数学Mathematics代写方面经验极为丰富,各种组合数学Combinatorial Mathematics相关的作业也就用不着 说。
我们提供的组合数学Combinatorial Mathematics及其相关学科的代写,服务范围广, 其中包括但不限于:
数学代写|组合数学作业代写Combinatorial Mathematics代考|The Inclusion-Exclusion Principle
“Sieve methods” are counting methods that within a universe allow only a desired set to survive a process of overcounting and undercounting. The InclusionExclusion Principle is the most common sieve and is our focus. Knuth attributed it to Doctrine of Chances by de Moivre [1718]. Riordan [1958] wrote
The logical identity on which it rests is very old; Dickson’s History of the Theory of Numbers (vol. I, p. 119) mentions its appearance in a work by Daniel da Silva in 1854 , but Montmort’s solution in 1713 of a famous problem, known generally by its French name, “le problème des rencontres” … effectively uses it and it may have been known to the Bernoullis.
Montmort corresponded with Nicolaus Bernoulli on such topics during 1710-12.
Many elementary texts describe inclusion-exclusion as a way to count the elements in a union of sets. Summing the sizes of two sets counts the intersection twice, so $\left|A_{1} \cup A_{2}\right|=\left|A_{1}\right|+\left|A_{2}\right|-\left|A_{1} \cap A_{2}\right|$. For three sets, the computation is
$$
\begin{aligned}
&+\left|A_{1}\right|-\left|A_{1} \cap A_{2}\right| \
\left|A_{1} \cup A_{2} \cup A_{3}\right|=&+\left|A_{2}\right|-\left|A_{2} \cap A_{3}\right|+\left|A_{1} \cap A_{2} \cap A_{3}\right| . \
&+\left|A_{3}\right|-\left|A_{3} \cap A_{1}\right|
\end{aligned}
$$
数学代写|组合数学作业代写Combinatorial Mathematics代考|Pólya-Redfield Counting
When we count “distinguishable” objects, the objects are grouped into classes by an equivalence relation, and we count these classes. For example, we can form a string of $n$ beads drawn from $k$ types in $k^{n}$ ways, but when we join the ends to make a necklace, the necklaces obtained from it by cyclic rotations and flips are indistinguishable from it.
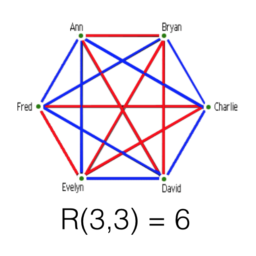
A classical application counts the isomorphism classes of $n$-vertex graphs. There are $2^{\left(\begin{array}{l}n \ 2\end{array}\right)}$ graphs with vertex set $[n]$, but two graphs are isomorphic when a vertex permutation turns one into the other. Since bijections can be composed or inverted, isomorphism is an equivalence relation. To view this as a “distinguishable colorings” problem, we view vertex pairs as colored by “edge” or “non-edge”.
Two simple examples introduce the technique.
数学代写|组合数学作业代写COMBINATORIAL MATHEMATICS代考|Permutations and Tabl
The subject of Young tableaux expands upon our discussions of permutations, partitions of integers, and bijections. Young tableaux correspond to representations of the symmetric group and are central in the study of symmetric functions (see Sagan [1991], Fulton [1997], and Stanley [1999]). We confine our attention to their enumeration and their connections to monotone sublists in permutations.
THE HOOK-LENGTH FORMULA
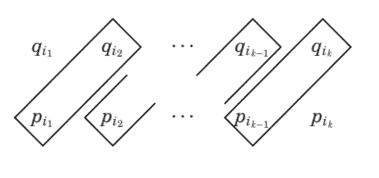
A generalization of Bertrand’s Ballot Problem considers $m$ candidates instead of two. Candidate $i$ receives $\lambda_{i}$ votes, with $\lambda_{1} \geq \cdots \geq \lambda_{m}$ and $\sum \lambda_{i}=n$. What is the probability that the partial vote totals always maintain the same order while the votes are being counted?
Record $j$ in the row for the candidate receiving the $j$ th vote. At the end the elements of $[n]$ occupy the positions in the Ferrers diagram for a partition $\lambda$. By construction, the numbers increase in each row. Partial votes totals satisfy the stated condition if and only if each candidate reaches $k$ votes before the next candidate does; thus the numbers must also increase in each column, as shown below. To solve our problem, we divide the number of such tableaux for $\lambda$ by the multinomial coefficient $\left(\begin{array}{c}n \ \lambda_{1}, \ldots, \lambda_{m}\end{array}\right)$, which counts all vote sequences.
$$
\begin{aligned}
&1357 \
&248 \
&69
\end{aligned}
$$
组合数学代写
数学代写|组合数学作业代写COMBINATORIAL MATHEMATICS代考|THE INCLUSION-EXCLUSION PRINCIPLE
“筛法”是一种计数方法,它在一个全域内只允许所需的集合在多算和少算的过程中幸存下来。包含排除原则是最常见的筛子,也是我们关注的重点。Knuth 将其归因于 de Moivre 的机会学说1718. 里奥丹1958写
它所依赖的逻辑恒等式非常古老;迪克森的数论史在这l.一世,p.119在 1854 年丹尼尔·达席尔瓦 (Daniel da Silva) 的作品中提到了它的出现,但蒙莫特 (Montmort) 在 1713 年解决了一个著名问题,通常以其法语名称“le problème des rencontres”而闻名……有效地使用了它,而且伯努利家族可能已经知道它。
在 1710-12 年间,蒙莫特与尼古拉斯·伯努利就这些话题进行了通信。
许多基本文本将包含-排除描述为一种计算集合中元素的方法。将两个集合的大小相加计算交集两次,所以|一种1∪一种2|=|一种1|+|一种2|−|一种1∩一种2|. 对于三组,计算为
$$
\begin{aligned}
&+\left|A_{1}\right|-\left|A_{1} \cap A_{2}\right| \
\left|A_{1} \cup A_{2} \cup A_{3}\right|=&+\left|A_{2}\right|-\left|A_{2} \cap A_{3}\right|+\left|A_{1} \cap A_{2} \cap A_{3}\right| . \
&+\left|A_{3}\right|-\left|A_{3} \cap A_{1}\right|
\end{aligned}
$$
数学代写|组合数学作业代写COMBINATORIAL MATHEMATICS代考|PÓLYA-REDFIELD COUNTING
当我们计算“可区分的”对象时,这些对象通过等价关系分组到类中,然后我们计算这些类。例如,我们可以形成一个字符串n珠子取自ķ输入ķn方法,但是当我们将两端连接起来制作项链时,通过循环旋转和翻转从中获得的项链与它没有区别。
一个经典的应用程序计算同构类n-顶点图。有2(n 2)带顶点集的图[n],但是当顶点置换将一个变为另一个时,两个图是同构的。由于双射可以组合或反转,所以同构是等价关系。为了将其视为“可区分着色”问题,我们将顶点对视为由“边缘”或“非边缘”着色。
两个简单的例子介绍了这项技术。
数学代写|组合数学作业代写COMBINATORIAL MATHEMATICS代考|PERMUTATIONS AND TABL
Young tableaux 的主题扩展了我们对排列、整数分区和双射的讨论。年轻的画面对应于对称群的表示,是对称函数研究的核心s和和小号一种G一种n[1991],F在l吨这n[1997],一种nd小号吨一种nl和是[1999]. 我们将注意力集中在它们的枚举以及它们与排列中的单调子列表的联系上。
钩长公式
Bertrand 选票问题的一般化考虑米候选人而不是两个。候选人一世收到λ一世票,与λ1≥⋯≥λ米和∑λ一世=n. 在计票时,部分投票总数始终保持相同顺序的概率是多少?
记录j在接受该候选人的行中j投票。最后的元素[n]在 Ferrers 图中占据分区的位置λ. 通过构造,每行的数字都会增加。当且仅当每个候选人达到ķ在下一位候选人之前投票;因此,每列中的数字也必须增加,如下所示。为了解决我们的问题,我们将此类画面的数量划分为λ由多项式系数(n λ1,…,λ米),它计算所有投票序列。

数学代写|组合数学作业代写Combinatorial Mathematics代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。