如果你也在 怎样代写偏微分方程Partial Differential Equations这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。偏微分方程Partial Differential Equations是一个方程,它规定了一个多变量函数的各种偏导数之间的关系。该函数通常被认为是一个有待解决的 “未知数”,类似于x被认为是代数方程(如x2-3x+2=0)中有待解决的一个未知数。因此,在现代数学和科学研究中,有大量使用计算机对某些偏微分方程的解进行数值近似的方法。
偏微分方程Partial Differential Equations在以数学为导向的科学领域,如物理学和工程学中无处不在。例如,它们是现代科学对声音、热量、扩散、静电、电动力学、热力学、流体动力学、弹性、广义相对论和量子力学(薛定谔方程、保利方程等)的基础性认识。它们也产生于许多纯粹的数学考虑,如微分几何和变分计算;在其他值得注意的应用中,它们是几何拓扑学中证明庞加莱猜想的基本工具。
my-assignmentexpert™ 偏微分方程Partial Differential Equations作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的偏微分方程Partial Differential Equations作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此偏微分方程Partial Differential Equations作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的偏微分方程Partial Differential Equations代写服务。我们的专家在数学Mathematics代写方面经验极为丰富,各种偏微分方程Partial Differential Equations相关的作业也就用不着 说。
我们提供的偏微分方程Partial Differential Equations及其相关学科的代写,服务范围广, 其中包括但不限于:
调和函数 harmonic function
椭圆方程 elliptic equation
抛物方程 Parabolic equation
双曲方程 Hyperbolic equation
非线性方法 nonlinear method
变分法 Calculus of Variations
几何分析 geometric analysis
偏微分方程数值解 Numerical solution of partial differential equations

数学代写|偏微分方程作业代写Partial Differential Equations代考|Conservation of Mass and the Continuity Equation
Consider the fluid inside a set fixed piece $W \subseteq \Omega$.
The mass of the fluid in $W$ at time $t$ is
$$
m_{W}(t):=\iiint_{W} \rho(x, y, z, t) d x d y d z .
$$
Note that $m_{W}(t)$ has dimensions of mass. We use differentiation under the integral sign (cf. Section A.9) to find that
$$
\frac{d m_{W}(t)}{d t}=\iiint_{W} \rho_{t}(x, y, z, t) d x d y d z .
$$
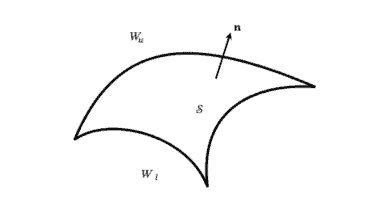
Now we ask the fundamental question: How can $m_{W}$, the total mass of fluid in $W$, change with time? The simple answer is that fluid can enter or leave $W$ across the boundary $\partial W$. At any point $(x, y, z)$ on the boundary and time $t$, the fluid flux across the boundary is instantaneously $\rho \mathbf{u} \cdot \mathbf{n}$, where $\mathbf{n}$ denotes the outer unit normal to $W$. Note that the fluid flux $\rho \mathbf{u} \cdot \mathbf{n}$ has dimensions of mass per unit area per unit time. The total (net) amount of fluid leaving $W$ at time $t$ is then
$$
\iint_{\partial W} \rho \mathbf{u} \cdot \mathbf{n} d S .
$$
Note that the above has dimensions of mass per unit time. Balancing (2.54) with (2.55), we find
$$
\iiint_{W} \rho_{t}(x, y, z, t) d x d y d z=-\iint_{\partial W} \rho \mathbf{u} \cdot \mathbf{n} d S .
$$
数学代写|偏微分方程作业代写Partial Differential Equations代考|Conservation of Linear Momentum and Pressure
We now turn to the conservation of linear momentum (mass $\times$ velocity). This conservation principle is dictated by Newton’s Second Law which states that the rate of change of linear momentum must be balanced by the net forces. Let us first motivate why computing the time rate of change of linear momentum is far more complicated than simply taking the partial derivative with respect to $t$. We already implicitly addressed this in deriving the continuity equation but it is useful to focus on this point for spatial descriptions of velocity and acceleration. If you are familiar with the notion of a material derivative (cf. Section 2.8.6), or comfortable with the derivation of the continuity equation, you may skip the following comment (digression).
数学代写|偏微分方程作业代写PARTIAL DIFFERENTIAL EQUATIONS代考|Gas Dynamics: The Compressible Euler Equations
We consider an ideal gas, for example air. A gas is an example of a compressible fluid; as a set region of the fluid (a set collection of fluid particles) moves with time, its volume can change. Alternatively, the density of the fluid can vary with space and time. So what is pressure $p$ in a gas? Is it an additional state variable which we need the PDEs to solve for? No, for a compressible fluid, the pressure at any point and time is a function of the density; that is,
$$
p(x, y, z, t)=f(\rho(x, y, z, t)),
$$
for some function $f$. As you might expect, $f$ is an increasing function as, intuitively, the greater the density the greater the pressure. The particular choice of function will depend on the exact nature of the gas. For many gases, the function $f$ is simply a power law; i.e., $f(\rho)=c_{0} \rho^{\gamma}$, for some constants $c_{0}>0$ and $\gamma>0$.
Substituting (2.64) into (2.63), we arrive at the compressible Euler equations:
$$
\left{\begin{array}{l}
\frac{\partial \mathbf{u}}{\partial t}+\mathbf{u} \cdot \nabla \mathbf{u}=-\frac{1}{\rho} \nabla f(\rho) \
\frac{\partial \rho}{\partial t}+\operatorname{div}(\rho \mathbf{u})=0
\end{array}\right.
$$
These are equations for gas dynamics and consist of a system of four partial differential equations in four unknown state variables $\left(\rho, u_{1}, u_{2}, u_{3}\right)$. These Euler equations are quasilinear first order. The reader should note the parallel to the inviscid Burgers equation in $1 \mathrm{D}\left(u u_{x}\right.$ vs. $\left.\mathbf{u} \cdot \nabla \mathbf{u}\right)$. Indeed, discontinuities and shock waves are signature solutions to these equations of gas dynamics.
偏微分方程代写
数学代写|偏微分方程作业代写PARTIAL DIFFERENTIAL EQUATIONS代考|CONSERVATION OF MASS AND THE CONTINUITY EQUATION
考虑一组固定件内的流体在⊆Ω.
中流体的质量在有时吨是
米在(吨):=∭在ρ(X,是,和,吨)dXd是d和.
注意米在(吨)有质量的维度。我们在积分符号下使用微分CF.小号和C吨一世这n一种.9找到那个
d米在(吨)d吨=∭在ρ吨(X,是,和,吨)dXd是d和.
现在我们问一个基本的问题:如何米在, 流体的总质量在,随时间变化?简单的答案是流体可以进入或离开在越过边界∂在. 在任何时候(X,是,和)在边界和时间上吨, 穿过边界的流体通量是瞬时的ρ在⋅n, 在哪里n表示外部单位法线在. 注意流体通量ρ在⋅n具有每单位时间每单位面积的质量量纲。总数n和吨流出的液体量在有时吨那么是
∬∂在ρ在⋅nd小号.
请注意,以上具有每单位时间的质量尺寸。平衡2.54和2.55, 我们发现
∭在ρ吨(X,是,和,吨)dXd是d和=−∬∂在ρ在⋅nd小号.
数学代写|偏微分方程作业代写PARTIAL DIFFERENTIAL EQUATIONS代考|CONSERVATION OF LINEAR MOMENTUM AND PRESSURE
我们现在转向线性动量守恒米一种ss$×$在和l这C一世吨是. 这一守恒定律由牛顿第二定律规定,该定律指出线性动量的变化率必须由净力平衡。让我们首先说明为什么计算线性动量的时间变化率远比简单地对吨. 我们在推导连续性方程时已经隐含地解决了这个问题,但是关注这一点对于速度和加速度的空间描述是有用的。如果您熟悉材料导数的概念CF.小号和C吨一世这n2.8.6,或者对连续性方程的推导感到满意,您可以跳过以下评论d一世Gr和ss一世这n.
数学代写|偏微分方程作业代写PARTIAL DIFFERENTIAL EQUATIONS代考|GAS DYNAMICS: THE COMPRESSIBLE EULER EQUATIONS
我们考虑一种理想气体,例如空气。气体是可压缩流体的一个例子;作为流体的一组区域一种s和吨C这ll和C吨一世这n这FFl在一世dp一种r吨一世Cl和s随着时间的推移,它的体积会发生变化。或者,流体的密度可以随空间和时间而变化。那么什么是压力p在气体中?它是我们需要 PDE 解决的附加状态变量吗?不,对于可压缩流体,任何点和时间的压力都是密度的函数;那是,
p(X,是,和,吨)=F(ρ(X,是,和,吨)),
对于某些功能F. 如你所料,F是一个递增函数,直观地说,密度越大,压力越大。功能的具体选择将取决于气体的确切性质。对于许多气体,函数F只是幂律;IE,F(ρ)=C0ρC, 对于一些常数C0>0和C>0.
替代2.64进入2.63,我们得到可压缩的欧拉方程:
$$
\left{∂在∂吨+在⋅∇在=−1ρ∇F(ρ) ∂ρ∂吨+div(ρ在)=0\对。
$$
这些是气体动力学方程,由四个未知状态变量的四个偏微分方程组成(ρ,在1,在2,在3). 这些欧拉方程是拟线性的一阶。读者应注意与无粘性 Burgers 方程的平行关系1D(在在X对比在⋅∇在). 事实上,不连续性和冲击波是这些气体动力学方程的标志性解。

数学代写|偏微分方程作业代写Partial Differential Equations代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。