如果你也在 怎样代写泛函分析functional analysis这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。泛函分析functional analysis是数学分析的一个分支,其核心是研究具有某种极限相关结构(如内积、规范、拓扑等)的向量空间以及定义在这些空间上并在适当意义上尊重这些结构的线性函数。函数分析的历史根源在于对函数空间的研究,以及对函数变换属性的表述,例如将傅里叶变换作为定义函数空间之间的连续、单元等算子的变换。这一观点对微分和积分方程的研究特别有用。
泛函分析functional analysis这个词作为一个名词的用法可以追溯到变分学,意味着一个参数是函数的函数。这个词最早是在哈达玛德1910年关于该主题的书中使用的。然而,函数的一般概念早在1887年就由意大利数学家和物理学家Vito Volterra提出。非线性函数的理论由Hadamard的学生,特别是Fréchet和Lévy继续研究。哈达玛德还创立了现代线性函数分析学派,该学派由里耶兹和斯特凡-巴纳赫周围的波兰数学家小组进一步发展。
my-assignmentexpert™ 泛函分析functional analysis作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的泛函分析functional analysis作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此泛函分析functional analysis作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的泛函分析functional analysis代写服务。我们的专家在数学Mathematics代写方面经验极为丰富,各种泛函分析functional analysis相关的作业也就用不着 说。
我们提供的泛函分析functional analysis及其相关学科的代写,服务范围广, 其中包括但不限于:
非线性方法 nonlinear method functional analysis
变分法 Calculus of Variations
数学代写|泛函分析作业代写functional analysis代考|Metrizable Topology and Connectedness
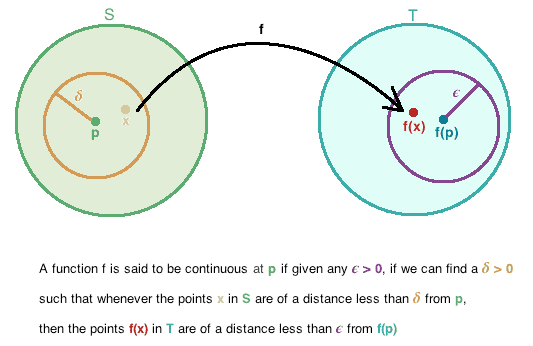
To begin with, we introduce the definition of a metric space followed by some useful examples, and consider topological properties such as open and closed sets induced by a metric space.
Definition 6.1.1. A metric space is a system $(X, d)$ that consists of a set $X$ whose elements are called points and a function $d$ whose domain is all of $X \times X$ and whose range is in $[0, \infty)$ such that the following three properties hold:
(i) d(x, y) ≥ 0 for all x, y ∈ X and d(x, y) = 0 if and only if x = y;
(ii) d(x, y) = d(y, x) for every x, y ∈ X ;
(iii) d(x,z) ≤ d(x, y) +d(y,z) for every x, y,z ∈ X.
数学代写|泛函分析作业代写functional analysis代考|Completeness
To discuss the completeness of a metric space, we start with the definition of the convergence of a point sequence in the metric space.
A point sequence is a function from $\mathbf{N}$ into a metric space $(X, d)$; this is, it is a sequence whose terms are points in $X$. Since our principal examples of metric spaces are the Euclidean spaces and we use subscripts to designate the coordinates of points in $\mathbf{R}^{n}$, we use superscripts to index the terms of a point sequence $-\left{x^{(k)}\right}_{k=1}^{\infty}$ represents a point sequence in a metric space.
Definition 6.2.1. Given a metric space $(X, d)$. The point sequence $\left{x^{(k)}\right}_{k=1}^{\infty}$ in $X$ is said to converge to the point $x \in X$, denoted $\lim _{k \rightarrow \infty} x^{(k)}=x$, provided for every $\varepsilon>0$ there is an $N \in \mathbf{N}$ such that $d\left(x^{(k)}, x\right)<\varepsilon$ whenever $k>N$.
Our first task is to establish a connection between convergent point sequences and cluster points.
Theorem 6.2.2. Given a metric space $(X, d)$ and $A \subseteq X$. Then $x \in A^{\prime}$ if and only if there is a non-repeating point sequence in $A$ that converges to $x$.
数学代写|泛函分析作业代写FUNCTIONAL ANALYSIS代考|Compactness, Density and Separability
As for an expansion of the Heine-Borel property, we discuss the compactness, density and countability of sets in a given metric space.
The first important notion induced by the Heine-Borel property is that of compact sets. To see this picture clearly, we first consider two examples that enable us to describe some important and attractive results in the theory of functions.
Example 6.3.1. A set $K \subseteq \mathbf{R}^{n}$ is said to be compact provided every sequence in $K$ contains a subsequence that converges to a point in $K$. This notion can be characterized by the equivalence of the following three statements:
(i) $K$ is compact;
(ii) $K$ is closed and bounded;
(iii) Every open cover of $K$ has a finite subcover; that is, if $K \subseteq \cup_{\alpha \in I} G_{\alpha}$ where each $G_{\alpha}$ is an open subset of $\mathbf{R}^{n}$, then there is a finite subset $J$ of the index set $I$ such that $K \subseteq \cup_{\alpha \in J} G_{\alpha}$.
In fact, suppose that (i) holds. Then every convergent sequence in $K$ converges to a point in $K$. Using the fact that a subset $E$ of $\mathbf{R}^{n}$ is closed if and only if $E$ equals its closure, we get that $K$ is closed. If $K$ is not bounded, then for each $k \in \mathbf{N}$, there is an $x_{k} \in K$ such that $d_{n}\left(x_{k}, 0\right)>k$. Consequently, no subsequence of $\left(x_{k}\right)_{k=1}^{\infty}$ can converge and so $K$ is not compact, a contradiction. Thus, (ii) holds.
泛函分析代写
数学代写|泛函分析作业代写FUNCTIONAL ANALYSIS代考|METRIZABLE TOPOLOGY AND CONNECTEDNESS
首先,我们介绍度量空间的定义以及一些有用的示例,并考虑由度量空间引起的开集和闭集等拓扑性质。
定义 6.1.1。度量空间是一个系统(X,d)由一组组成X其元素称为点和函数d其域是全部X×X并且其范围在[0,∞)使得以下三个性质成立:
(i) d(x, y) ≥ 0 for all x, y ∈ X and d(x, y) = 0 if and only if x = y;
(ii) d(x, y) = d(y, x) for every x, y ∈ X ;
(iii) d(x,z) ≤ d(x, y) +d(y,z) for every x, y,z ∈ X.
数学代写|泛函分析作业代写FUNCTIONAL ANALYSIS代考|COMPLETENESS
为了讨论度量空间的完整性,我们从度量空间中点序列收敛的定义开始。
点序列是一个函数ñ进入度量空间(X,d); 也就是说,它是一个序列,其项是点X. 因为我们的度量空间的主要例子是欧几里得空间,我们使用下标来指定点的坐标Rn,我们使用上标来索引一个点序列的项-\left{x^{(k)}\right}_{k=1}^{\infty}-\left{x^{(k)}\right}_{k=1}^{\infty}表示度量空间中的点序列。
定义 6.2.1。给定一个度量空间(X,d). 点序列\left{x^{(k)}\right}_{k=1}^{\infty}\left{x^{(k)}\right}_{k=1}^{\infty}在X据说收敛到一点X∈X, 表示林ķ→∞X(ķ)=X, 为每个e>0有一个ñ∈ñ这样d(X(ķ),X)<e每当ķ>ñ.
我们的首要任务是在收敛点序列和聚类点之间建立连接。
定理 6.2.2。给定一个度量空间(X,d)和一种⊆X. 然后X∈一种′当且仅当在一种收敛到X.
数学代写|泛函分析作业代写FUNCTIONAL ANALYSIS代考|COMPACTNESS, DENSITY AND SEPARABILITY
至于海涅-博雷尔性质的扩展,我们讨论了给定度量空间中集合的紧致性、密度和可数性。
Heine-Borel 属性引出的第一个重要概念是紧集。为了清楚地看到这幅图,我们首先考虑两个例子,它们使我们能够描述函数理论中一些重要且有吸引力的结果。
例 6.3.1。一套ķ⊆Rn据说是紧凑的,前提是每个序列ķ包含一个收敛到一个点的子序列ķ. 这个概念可以通过以下三个陈述的等价来表征:
一世 ķ紧凑;
一世一世 ķ是封闭且有界的;
一世一世一世每一个打开的盖子ķ有一个有限的子覆盖;也就是说,如果ķ⊆∪一种∈一世G一种其中每个G一种是的一个开子集Rn, 那么有一个有限子集Ĵ索引集的一世这样ķ⊆∪一种∈ĴG一种.
事实上,假设一世持有。然后每个收敛序列ķ收敛到一个点ķ. 使用子集的事实和的Rn关闭当且仅当和等于它的闭包,我们得到ķ已经关闭。如果ķ是无界的,那么对于每个ķ∈ñ, 有一个Xķ∈ķ这样dn(Xķ,0)>ķ. 因此,没有子序列(Xķ)ķ=1∞可以收敛等等ķ不紧凑,矛盾。因此,一世一世持有。

数学代写|泛函分析作业代写functional analysis代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。