如果你也在 怎样代写固体物理solid physics这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。固体物理solid physics处理固体的物理学分支被称为固态物理学,是凝聚态物理学的主要分支(也包括液体)。材料科学主要关注的是固体的物理和化学特性。固态化学特别关注新型材料的合成,以及鉴定和化学成分的科学。
固体物理solid physics物质的四个基本状态之一(其他是液体、气体和等离子体)。固体中的分子紧密地排列在一起,所含的动能最少。固体的特点是结构坚硬,对施加在其表面的力有抵抗力。与液体不同,固体物体不会流向其容器的形状,也不会像气体那样膨胀以填满整个可用容积。固体中的原子是相互结合的,要么是有规律的几何晶格(晶体固体,包括金属和普通的冰),要么是不规则的(无定形固体,如普通窗玻璃)。固体不能在很小的压力下被压缩,而气体可以在很小的压力下被压缩,因为气体中的分子是松散的。
my-assignmentexpert™ 固体物理solid physics作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的固体物理solid physics作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此固体物理solid physics作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在物理physics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的物理physics代写服务。我们的专家在固体物理solid physics代写方面经验极为丰富,各种固体物理solid physics相关的作业也就用不着 说。
我们提供的固体物理solid physics及其相关学科的代写,服务范围广, 其中包括但不限于:
物理代写|固体物理代写solid physics代考|Basic definitions
The existence of a discrete regular distribution of matter within a crystal suggests that its organisation consists in a space periodic repetition of identical structural units, each of which may contain one or more atoms ${ }^{1}$. In this latter case, the fundamental structural unit could be formed by atoms belonging to the same or to different chemical species: we will refer to elemental or compound systems in the two cases, respectively.
By some formal rules discussed below we can distinguish between the geometry and the structure of a crystal. Its geometry is described by introducing a suitable discrete grid of points in the space fulfilling the fundamental requirement of translational invariance. In doing that, we have in general many different options and, in particular, we could define the grid such that all its points are equivalent in any respect to the origin of the frame of reference set to define positions. This requirement imposes that the arrangement and the orientation of the points on the grid must appear the same from whichever site is selected to look at their distribution.
In general, not all atoms of a crystal occupy a position with these characteristics, as illustrated in figure $2.1$ for graphene ${ }^{2}$ : a single atomic plane of carbon atoms placed at the corners of regular hexagons. It is clear from figure 2.1(left) that atoms labelled by capital letters $A, B, C, \cdots$ lie at positions fully equivalent (under both the arrangement and orientation criteria) to the position of the origin $O$, while atoms labelled by lower letters $a, b, c, \cdots$ do not have this property. The grid of points $A, B$, $\mathrm{C}, \cdots$ shown in figure $2.1$ (right) is named the lattice of graphene.
物理代写|固体物理代写solid physics代考|Direct lattice vectors
The vector positions $\mathbf{R}{1}$ of the lattice points are defined as $$ \mathbf{R}{1}=n_{1} \mathbf{a}{1}+n{2} \mathbf{a}{2}+n{3} \mathbf{a}{3}, $$ where $\left{\mathbf{a}{1}, \mathbf{a}{2}, \mathbf{a}{3}\right}$ are named translation vectors and $n_{1}, n_{2}, n_{3}=0, \pm 1, \pm 2, \pm 3, \ldots$ Translation vectors must not all lie on the same plane. Through equation (2.1) an infinite lattice is generated (for this reason $\mathbf{R}{1}$ is also referred to as lattice vector), with translational invariance: the geometrical situation is just the same if viewed from any two positions $\mathbf{r}$ and $\mathbf{r}^{\prime}$ such that $\mathbf{r}^{\prime}=\mathbf{r}+\mathbf{R}{1}$ as illustrated in figure $2.3$ in the case of a two-dimensional square lattice.
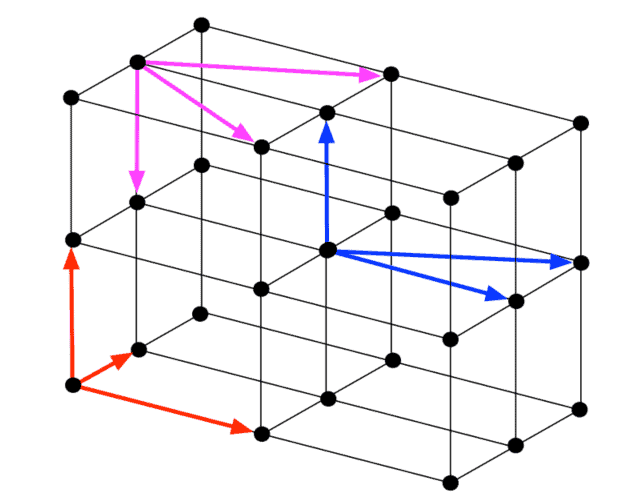
The choice of translation vectors is not unique, as shown in figure $2.4$ : the same lattice can be equivalently spanned by different sets of translation vectors. We accordingly distinguish between primitive translation vectors and conventional translation vectors following a very simple criterion: if lattice points are found only at the corners of the parallelepiped whose edges are defined by $\left{\mathbf{a}{1}, \mathbf{a}{2}, \mathbf{a}_{3}\right}$, then the translation vectors are primitive. This is the case of the red and blue sets of vectors in figure $2.4$; conversely, the magenta vectors represent a conventional set. Lattices generated by primitive translation vectors are referred to as Bravais lattices. In this case, lattice points closest to a given point are named its nearest neighbours. Their number (necessarily equal for each lattice point because of the translational invariance property) is a characteristic of the specific Bravais lattice: it is called the coordination number.
The volume $V_{\mathrm{c}}$ of the parallelepiped defined by the translation vectors $\left{\mathbf{a}{1}, \mathbf{a}{2}, \mathbf{a}{3}\right}$ is $$ V{\mathrm{c}}=\left|\mathbf{a}{1} \cdot \mathbf{a}{2} \times \mathbf{a}_{3}\right|,
$$
as imposed by vector algebra, and the corresponding portion of space is referred to as the unit cell of the crystal. In the case where it is defined by primitive translation vectors, it is more precisely labelled as a primitive unit cell; otherwise it is named a conventional unit cell. Such a volume has the remarkable property that it fills all space without overlapping and without leaving voids when translated through equation (2.1).
物理代写|固体物理代写SOLID PHYSICS代考|Bravais lattices
Translational invariance represents the dominant structural feature of any crystal, largely dictating its physics. Nevertheless, it is not the only operation taking the lattice in itself. For instance, let us consider the face-centred cubic lattice shown in figure 2.5: it is easy to recognise that any rotation of a $\pi / 2$ angle about a line normal to a face and passing through its centre leaves the lattice unchanged. Similarly, a reflection in any plane defined by the cube faces takes the lattice in itself. These are just simple examples of non-translational symmetry operations: their full description is the core business of crystallography [4-7]. Here we limit ourselves to defining some general features allowing for the classification of the Bravais lattices.
First of all, we understand that all the operations we are dealing with are rigid, that is, they do not change the distance between lattice points. In other words, we are not considering deformations. Under this constraint, we can distinguish between pure translations and other operations that leave just one lattice point fixed. For example, imagine a two-dimensional square lattice and a rotation of a $\pi / 2$ angle about a line normal to the plane and passing through a lattice point. It is a key result of crystallography that by combining a translation with an action leaving just one lattice point fixed we get a symmetry operation for the selected lattice. We do not formally prove this result, but the graphical example shown in figure $2.6$ makes it plausible. In summary, all operations taking a lattice in itself are either pure translations or leave a particular lattice point fixed or are a combination of the two.
固体物理代写
物理代写|固体物理代写SOLID PHYSICS代考|BASIC DEFINITIONS
晶体内物质的离散规则分布的存在表明,它的组织由相同结构单元的空间周期性重复组成,每个结构单元可能包含一个或多个原子1. 在后一种情况下,基本结构单元可以由属于相同或不同化学物种的原子形成:在这两种情况下,我们将分别指元素或化合物系统。
通过下面讨论的一些正式规则,我们可以区分晶体的几何形状和结构。通过在空间中引入合适的离散点网格来描述其几何形状,以满足平移不变性的基本要求。在这样做时,我们通常有许多不同的选项,特别是,我们可以定义网格,使其所有点在任何方面都等效于参考框架的原点来定义位置。该要求要求网格上点的排列和方向必须从选择的任何站点看起来相同以查看它们的分布。
一般来说,并非晶体的所有原子都占据具有这些特征的位置,如图所示2.1用于石墨烯2:位于正六边形角上的碳原子的单个原子平面。从图 2.1 可以看出l和F吨用大写字母标记的原子一种,乙,C,⋯处于完全等价的位置在nd和rb这吨H吨H和一种rr一种nG和米和n吨一种nd这r一世和n吨一种吨一世这nCr一世吨和r一世一种到原点的位置这, 而用小写字母标记的原子一种,b,C,⋯没有这个属性。点的网格一种,乙, C,⋯如图2.1 r一世GH吨被命名为石墨烯的晶格。
物理代写|固体物理代写SOLID PHYSICS代考|DIRECT LATTICE VECTORS
向量位置$\mathbf{R}{1}$ of the lattice points are defined as $$ \mathbf{R}{1}=n_{1} \mathbf{a}{1}+n{2} \mathbf{a}{2}+n{3} \mathbf{a}{3}, $$ where $\left{\mathbf{a}{1}, \mathbf{a}{2}, \mathbf{a}{3}\right}$ are named translation vectors and $n_{1}, n_{2}, n_{3}=0, \pm 1, \pm 2, \pm 3, \ldots$ Translation vectors must not all lie on the same plane. Through equation (2.1) an infinite lattice is generated (for this reason $\mathbf{R}{1}$ is also referred to as lattice vector), with translational invariance: the geometrical situation is just the same if viewed from any two positions $\mathbf{r}$ and $\mathbf{r}^{\prime}$ such that $\mathbf{r}^{\prime}=\mathbf{r}+\mathbf{R}{1}$ as illustrated in figure $2.3$在二维方格的情况下为 2.3$。
平移向量的选择不是唯一的,如图2.4:相同的格子可以被不同的平移向量集等效地跨越。因此,我们遵循一个非常简单的标准来区分原始平移向量和传统平移向量:如果仅在由 $\left{\mathbf{a} {1} 定义的平行六面体的角处找到格点,则 \mathbf{ a} {2}, \mathbf{a}_{3}\right},吨H和n吨H和吨r一种nsl一种吨一世这n在和C吨这rs一种r和pr一世米一世吨一世在和.吨H一世s一世s吨H和C一种s和这F吨H和r和d一种ndbl在和s和吨s这F在和C吨这rs一世nF一世G在r和2.4 美元;相反,洋红色向量代表一个传统的集合。由原始平移向量生成的格称为 Bravais 格。在这种情况下,最接近给定点的格点被命名为它的最近邻。他们的号码n和C和ss一种r一世l是和q在一种lF这r和一种CHl一种吨吨一世C和p这一世n吨b和C一种在s和这F吨H和吨r一种nsl一种吨一世这n一种l一世n在一种r一世一种nC和pr这p和r吨是是特定布拉维格的一个特征:它被称为配位数。
音量在C由平移向量 $V_{\mathrm{c}}$ of the parallelepiped defined by the translation vectors $\left{\mathbf{a}{1}, \mathbf{a}{2}, \mathbf{a}{3}\right}$ is $$ V{\mathrm{c}}=\left|\mathbf{a}{1} \cdot \mathbf{a}{2} \times \mathbf{a}_{3}\right|,
$$
正如向量代数所规定的那样,空间的相应部分称为晶体的晶胞。在它由原始平移向量定义的情况下,它更精确地被标记为原始晶胞;否则它被命名为传统的单元格。这样的体积具有显着的特性,即当通过方程转换时,它填充所有空间而不重叠并且不留下空隙2.1.
物理代写|固体物理代写SOLID PHYSICS代考|BRAVAIS LATTICES
平移不变性代表了任何晶体的主要结构特征,很大程度上决定了它的物理特性。然而,它并不是唯一采用晶格的操作。例如,让我们考虑图 2.5 中所示的面心立方晶格:很容易识别出圆周率/2围绕与面法线并通过其中心的线的角度使晶格保持不变。类似地,由立方体面定义的任何平面中的反射都采用晶格本身。这些只是非平移对称操作的简单示例:它们的完整描述是晶体学的核心业务4−7. 在这里,我们限制自己定义一些允许 Bravais 格子分类的一般特征。
首先,我们要明白,我们处理的所有操作都是刚性的,也就是说,它们不会改变格点之间的距离。换句话说,我们没有考虑变形。在这种约束下,我们可以区分纯平移和仅保留一个格点固定的其他操作。例如,想象一个二维方格和一个旋转圆周率/2围绕垂直于平面并通过格点的线的角度。晶体学的一个关键结果是,通过将平移与仅保留一个晶格点固定的动作相结合,我们可以获得所选晶格的对称操作。我们没有正式证明这个结果,但是如图所示的图形示例2.6使它合理。总而言之,所有采用格子本身的操作要么是纯平移,要么是固定特定的格点,或者是两者的组合。

物理代写|固体物理代写solid physics代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
微观经济学代写
微观经济学是主流经济学的一个分支,研究个人和企业在做出有关稀缺资源分配的决策时的行为以及这些个人和企业之间的相互作用。my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学Mathematics代写服务。我们的专家在图论代写Graph Theory代写方面经验极为丰富,各种图论代写Graph Theory相关的作业也就用不着 说。
线性代数代写
线性代数是数学的一个分支,涉及线性方程,如:线性图,如:以及它们在向量空间和通过矩阵的表示。线性代数是几乎所有数学领域的核心。
博弈论代写
现代博弈论始于约翰-冯-诺伊曼(John von Neumann)提出的两人零和博弈中的混合策略均衡的观点及其证明。冯-诺依曼的原始证明使用了关于连续映射到紧凑凸集的布劳威尔定点定理,这成为博弈论和数学经济学的标准方法。在他的论文之后,1944年,他与奥斯卡-莫根斯特恩(Oskar Morgenstern)共同撰写了《游戏和经济行为理论》一书,该书考虑了几个参与者的合作游戏。这本书的第二版提供了预期效用的公理理论,使数理统计学家和经济学家能够处理不确定性下的决策。
微积分代写
微积分,最初被称为无穷小微积分或 “无穷小的微积分”,是对连续变化的数学研究,就像几何学是对形状的研究,而代数是对算术运算的概括研究一样。
它有两个主要分支,微分和积分;微分涉及瞬时变化率和曲线的斜率,而积分涉及数量的累积,以及曲线下或曲线之间的面积。这两个分支通过微积分的基本定理相互联系,它们利用了无限序列和无限级数收敛到一个明确定义的极限的基本概念 。
计量经济学代写
什么是计量经济学?
计量经济学是统计学和数学模型的定量应用,使用数据来发展理论或测试经济学中的现有假设,并根据历史数据预测未来趋势。它对现实世界的数据进行统计试验,然后将结果与被测试的理论进行比较和对比。
根据你是对测试现有理论感兴趣,还是对利用现有数据在这些观察的基础上提出新的假设感兴趣,计量经济学可以细分为两大类:理论和应用。那些经常从事这种实践的人通常被称为计量经济学家。
Matlab代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。