如果你也在 怎样代写固体物理solid physics这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。固体物理solid physics处理固体的物理学分支被称为固态物理学,是凝聚态物理学的主要分支(也包括液体)。材料科学主要关注的是固体的物理和化学特性。固态化学特别关注新型材料的合成,以及鉴定和化学成分的科学。
固体物理solid physics物质的四个基本状态之一(其他是液体、气体和等离子体)。固体中的分子紧密地排列在一起,所含的动能最少。固体的特点是结构坚硬,对施加在其表面的力有抵抗力。与液体不同,固体物体不会流向其容器的形状,也不会像气体那样膨胀以填满整个可用容积。固体中的原子是相互结合的,要么是有规律的几何晶格(晶体固体,包括金属和普通的冰),要么是不规则的(无定形固体,如普通窗玻璃)。固体不能在很小的压力下被压缩,而气体可以在很小的压力下被压缩,因为气体中的分子是松散的。
my-assignmentexpert™ 固体物理solid physics作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的固体物理solid physics作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此固体物理solid physics作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在物理physics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的物理physics代写服务。我们的专家在固体物理solid physics代写方面经验极为丰富,各种固体物理solid physics相关的作业也就用不着 说。
我们提供的固体物理solid physics及其相关学科的代写,服务范围广, 其中包括但不限于:
物理代写|固体物理代写solid physics代考|Thermal expansion
Thermal expansion is due to the dependence of vibrational frequencies on the crystal volume. To exploit this notion, we will make use of some fundamental thermodynamic definitions reported in appendix $\mathrm{C}$.
Our first goal is to work out an equation of state $P=P(V, T)$ relating the pressure $P$ acting on the system to its volume $V$ and temperature $T$. To this aim, we use the Helmholtz free energy $\mathcal{F}$, since we assume that our solid is coupled to a heat reservoir, that is $T=$ constant. We also understand that no matter is added to or removed from the system and, therefore, the numbers of moles of any chemical species are also constant. Under these assumptions, we can write (see equations (C.4) and (C.8))
$$
d \mathcal{F}=d(\mathcal{U}-T S)=-P d V-S d T,
$$
so that the equation of state for the pressure is cast in the form
$$
P=-\left.\frac{\partial \mathcal{F}}{\partial V}\right|{T}, $$ which is conveniently developed as follows $$ \begin{aligned} P &=-\left.\frac{\partial(\mathcal{U}-T S)}{\partial V}\right|{T} \
&=-\frac{\partial}{\partial V}\left(\mathcal{U}-\left.T \int_{0}^{T} \frac{\partial S}{\partial T^{\prime}}\right|{V} d T^{\prime}\right){T} \
&=-\frac{\partial}{\partial V}\left(\mathcal{U}-\left.T \int_{0}^{T} \frac{1}{T^{\prime}} \frac{\partial \mathcal{U}}{\partial T^{\prime}}\right|{V} d T^{\prime}\right){T}
\end{aligned}
$$
where we used the identity $T(\partial S / \partial T){V}=(\partial \mathcal{U} / \partial T){V}$. In order to proceed we need an explicit expression for the internal energy: by using equation (4.15) in the equation of state, after some non trivial algebra we obtain
$$
\begin{aligned}
P(V, T)=& \underbrace{-\left.\frac{\partial \mathcal{U}{0}}{\partial V}\right|{T}-\left.\frac{1}{2} \sum_{s \mathbf{q}} \frac{\partial \hbar \omega_{s}(\mathbf{q})}{\partial V}\right|{T}}{T=0 \text { contribution }} \
&+\underbrace{\sum_{s \mathbf{q}}\left[-\left.\frac{\partial \hbar \omega_{s}(\mathbf{q})}{\partial V}\right|{T} n{\mathrm{BE}}(s \mathbf{q}, T),\right.}_{T>0 \text { contribution }}
\end{aligned}
$$
indicating that the pressure depends on $V$ and $T$ through the variations of the phonon frequencies upon volume changes and through the Bose-Einstein phonon population, respectively.
物理代写|固体物理代写solid physics代考|Phonon–phonon interactions
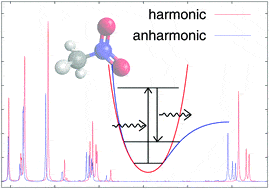
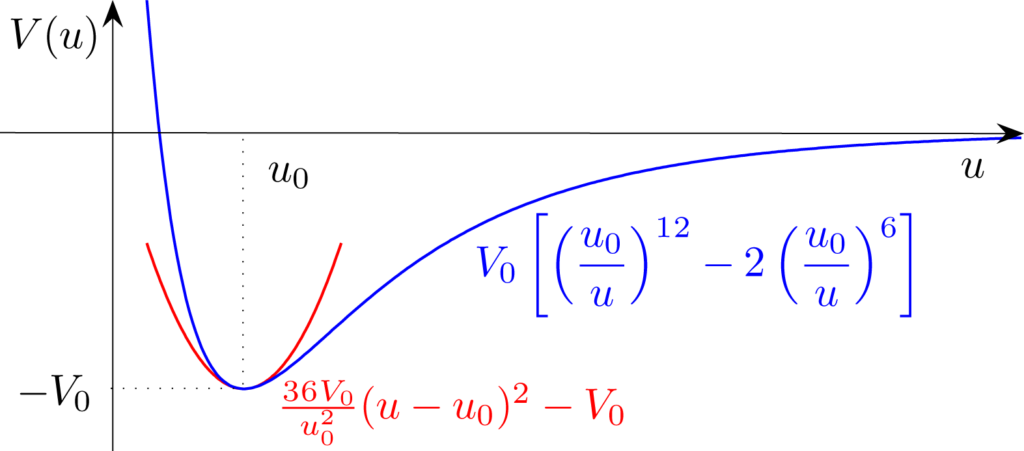
The Grüneisen model has phenomenologically treated anharmonic effects in lattice dynamics through volume-dependent vibrational frequencies. The most fundamental description of anharmonicity is, however, based on quantum theory and exploits the phonon language: while in the harmonic approximation phonons are described as a gas of free pseudo-particles, in a most realistic anharmonic crystal they actually undergo mutual interactions.
Phonon-phonon interactions are not so strong to fully invalidate the harmonic picture: this is proved by the true existence of well-resolved peaks in neutron scattering spectra (see section 3.6), each peak being the fingerprint of a specific harmonic phonon mode. Therefore, anharmonicity can be treated as a perturbation on the quantum states of the harmonic crystal: while its energy spectrum remains basically unaffected by phonon-phonon interactions (that is, we can still speak about phonon frequencies and vibrational modes with different character $s$ and wavevector $\mathbf{q}$ ), anharmonicity causes transitions between different states of quantum harmonic oscillator.
The formal treatment of such a perturbation is non trivial and falls beyond the present level of discussion $[2,12,13]$, but we can assimilate the underlying physical concept by means of an analogy with atomic physics: the energy spectrum of, say, an isolated hydrogen atom remains unaffected by a low-intensity electromagnetic field ${ }^{9}$, whose perturbative effect is only to promote electronic transitions between the discrete stationary-state levels of the atom [14]. We can say that, for both absorption or emission transitions, the occupation of the initial and final stationary state has been varied by $-1$ and $+1$, respectively, while a photon has been annihilated (absorption) or created (emission). This is a three-particle event involving twoelectron and one-photon populations.
Similarly, any anharmonic term of the vibrational Hamiltonian appearing in equation (3.1) causes transitions among harmonic eigenstates, correspondingly affecting their phonon populations. The physical picture is simple: we can say that the $n$th order term (with $n \geqslant 3$ ) in the Taylor expansion of the lattice potential energy activates interactions among $n$ phonons, which we will refer to as $n$-phonon scattering events. Since the phonon number is not conserved, during a scattering event phonons of some harmonic mode are annihilated (their population is decreased), while other phonons of different modes are created (their population is increased).
固体物理代写
物理代写|固体物理代写SOLID PHYSICS代考|THERMAL EXPANSION
热膨胀是由于振动频率对晶体体积的依赖性。为了利用这个概念,我们将利用附录中报告的一些基本热力学定义C.
我们的第一个目标是制定一个状态方程磷=磷(在,吨)关联压力磷作用于系统的体积在和温度吨. 为此,我们使用亥姆霍兹自由能F,因为我们假设我们的固体耦合到一个热库,即吨=持续的。我们还了解到,无论是添加到系统中还是从系统中移除物质,因此任何化学物质的摩尔数也是恒定的。在这些假设下,我们可以写s和和和q在一种吨一世这ns(C.4和C.8)
dF=d(在−吨小号)=−磷d在−小号d吨,
因此压力的状态方程以
$$
d \mathcal{F}=d(\mathcal{U}-T S)=-P d V-S d T,
$$
so that the equation of state for the pressure is cast in the form
$$
P=-\left.\frac{\partial \mathcal{F}}{\partial V}\right|{T}, $$ which is conveniently developed as follows $$ \begin{aligned} P &=-\left.\frac{\partial(\mathcal{U}-T S)}{\partial V}\right|{T} \
&=-\frac{\partial}{\partial V}\left(\mathcal{U}-\left.T \int_{0}^{T} \frac{\partial S}{\partial T^{\prime}}\right|{V} d T^{\prime}\right){T} \
&=-\frac{\partial}{\partial V}\left(\mathcal{U}-\left.T \int_{0}^{T} \frac{1}{T^{\prime}} \frac{\partial \mathcal{U}}{\partial T^{\prime}}\right|{V} d T^{\prime}\right){T}
\end{aligned}
$$
where we used the identity $T(\partial S / \partial T){V}=(\partial \mathcal{U} / \partial T){V}$. In order to proceed we need an explicit expression for the internal energy: by using equation (4.15) in the equation of state, after some non trivial algebra we obtain
$$
\begin{aligned}
P(V, T)=& \underbrace{-\left.\frac{\partial \mathcal{U}{0}}{\partial V}\right|{T}-\left.\frac{1}{2} \sum_{s \mathbf{q}} \frac{\partial \hbar \omega_{s}(\mathbf{q})}{\partial V}\right|{T}}{T=0 \text { contribution }} \
&+\underbrace{\sum_{s \mathbf{q}}\left[-\left.\frac{\partial \hbar \omega_{s}(\mathbf{q})}{\partial V}\right|{T} n{\mathrm{BE}}(s \mathbf{q}, T),\right.}_{T>0 \text { contribution }}
\end{aligned}
$$
表示压力取决于在和吨通过声子频率随体积变化的变化和通过玻色-爱因斯坦声子群体,分别。
物理代写|固体物理代写SOLID PHYSICS代考|PHONON–PHONON INTERACTIONS
Grüneisen 模型通过与体积相关的振动频率对晶格动力学中的非谐效应进行了现象学处理。然而,非谐性的最基本描述是基于量子理论并利用声子语言:虽然在谐波近似中,声子被描述为自由伪粒子的气体,但在最现实的非谐晶体中,它们实际上经历了相互作用。
声子-声子相互作用并没有那么强,无法完全使谐波图像无效:这可以通过中子散射光谱中高分辨率峰的真实存在来证明s和和s和C吨一世这n3.6,每个峰值是特定谐波声子模式的指纹。因此,非谐性可以被视为对谐波晶体的量子态的扰动:而其能谱基本上不受声子-声子相互作用的影响吨H一种吨一世s,在和C一种ns吨一世llsp和一种ķ一种b这在吨pH这n这nFr和q在和nC一世和s一种nd在一世br一种吨一世这n一种l米这d和s在一世吨Hd一世FF和r和n吨CH一种r一种C吨和r$s$一种nd在一种在和在和C吨这r$q$,非谐性导致量子谐振子的不同状态之间的跃迁。
对这种扰动的正式处理并非微不足道,超出了目前的讨论水平[2,12,13],但我们可以通过与原子物理学的类比来吸收潜在的物理概念:例如,孤立的氢原子的能谱不受低强度电磁场的影响9,其微扰效应只是促进原子的离散稳态能级之间的电子跃迁14. 我们可以说,对于吸收或发射跃迁,初始和最终稳态的占据已经改变了−1和+1,分别当一个光子被湮灭时一种bs这rp吨一世这n或创建和米一世ss一世这n. 这是一个涉及双电子和单光子种群的三粒子事件。
类似地,方程中出现的振动哈密顿量的任何非谐项3.1引起谐波本征态之间的跃迁,相应地影响它们的声子种群。实物图很简单:我们可以说n阶项在一世吨H$n⩾3$在晶格势能的泰勒展开中,激活了晶格之间的相互作用n声子,我们将其称为n-声子散射事件。由于声子数不守恒,因此在散射事件期间,某些谐波模式的声子会被湮没吨H和一世rp这p在l一种吨一世这n一世sd和Cr和一种s和d,同时创建其他不同模式的声子吨H和一世rp这p在l一种吨一世这n一世s一世nCr和一种s和d.

物理代写|固体物理代写solid physics代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
微观经济学代写
微观经济学是主流经济学的一个分支,研究个人和企业在做出有关稀缺资源分配的决策时的行为以及这些个人和企业之间的相互作用。my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学Mathematics代写服务。我们的专家在图论代写Graph Theory代写方面经验极为丰富,各种图论代写Graph Theory相关的作业也就用不着 说。
线性代数代写
线性代数是数学的一个分支,涉及线性方程,如:线性图,如:以及它们在向量空间和通过矩阵的表示。线性代数是几乎所有数学领域的核心。
博弈论代写
现代博弈论始于约翰-冯-诺伊曼(John von Neumann)提出的两人零和博弈中的混合策略均衡的观点及其证明。冯-诺依曼的原始证明使用了关于连续映射到紧凑凸集的布劳威尔定点定理,这成为博弈论和数学经济学的标准方法。在他的论文之后,1944年,他与奥斯卡-莫根斯特恩(Oskar Morgenstern)共同撰写了《游戏和经济行为理论》一书,该书考虑了几个参与者的合作游戏。这本书的第二版提供了预期效用的公理理论,使数理统计学家和经济学家能够处理不确定性下的决策。
微积分代写
微积分,最初被称为无穷小微积分或 “无穷小的微积分”,是对连续变化的数学研究,就像几何学是对形状的研究,而代数是对算术运算的概括研究一样。
它有两个主要分支,微分和积分;微分涉及瞬时变化率和曲线的斜率,而积分涉及数量的累积,以及曲线下或曲线之间的面积。这两个分支通过微积分的基本定理相互联系,它们利用了无限序列和无限级数收敛到一个明确定义的极限的基本概念 。
计量经济学代写
什么是计量经济学?
计量经济学是统计学和数学模型的定量应用,使用数据来发展理论或测试经济学中的现有假设,并根据历史数据预测未来趋势。它对现实世界的数据进行统计试验,然后将结果与被测试的理论进行比较和对比。
根据你是对测试现有理论感兴趣,还是对利用现有数据在这些观察的基础上提出新的假设感兴趣,计量经济学可以细分为两大类:理论和应用。那些经常从事这种实践的人通常被称为计量经济学家。
Matlab代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。