如果你也在 怎样代写固体物理solid physics这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。固体物理solid physics处理固体的物理学分支被称为固态物理学,是凝聚态物理学的主要分支(也包括液体)。材料科学主要关注的是固体的物理和化学特性。固态化学特别关注新型材料的合成,以及鉴定和化学成分的科学。
固体物理solid physics物质的四个基本状态之一(其他是液体、气体和等离子体)。固体中的分子紧密地排列在一起,所含的动能最少。固体的特点是结构坚硬,对施加在其表面的力有抵抗力。与液体不同,固体物体不会流向其容器的形状,也不会像气体那样膨胀以填满整个可用容积。固体中的原子是相互结合的,要么是有规律的几何晶格(晶体固体,包括金属和普通的冰),要么是不规则的(无定形固体,如普通窗玻璃)。固体不能在很小的压力下被压缩,而气体可以在很小的压力下被压缩,因为气体中的分子是松散的。
my-assignmentexpert™ 固体物理solid physics作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的固体物理solid physics作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此固体物理solid physics作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在物理physics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的物理physics代写服务。我们的专家在固体物理solid physics代写方面经验极为丰富,各种固体物理solid physics相关的作业也就用不着 说。
我们提供的固体物理solid physics及其相关学科的代写,服务范围广, 其中包括但不限于:
物理代写|固体物理代写solid physics代考|Historical background
The energy content of a physical system is thermodynamically accounted for by its internal energy $\mathcal{U}$ (see appendix $\mathrm{C}$ ) whose derivative with respect to temperature
$$
\mathcal{C}{V}=\left.\frac{d \mathcal{U}}{d T}\right|{V},
$$
is known as the heat capacity at constant volume $V$ : it represents the amount of heat we need to quasi-statically provide in order to increase the system temperature by one degree.
The first attempts to derive a microscopic theory for $\mathcal{C}{V}$ in crystalline solids were developed at the dawn of the XXth century. In many respects, we can consider these investigations as the beginning of quantum solid state physics [1]. Developing a microscopic theory was certainly worthy of effort since the classical theory of $\mathcal{C}{V}$ is contradicted by the experimental evidence. In order to outline this theory, outdated but still valuable for our pedagogical approach to the thermal properties, we preliminarily remark that there are three main contributions to the heat capacity of a crystal, respectively, deriving from lattice vibrations, conduction electrons, and magnetic ordering. In non-magnetic insulators the first one is by far the leading one and in this chapter we focus just on it ${ }^{1}$.
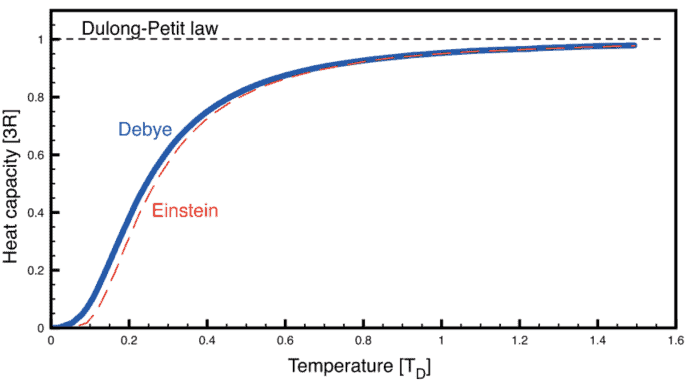
物理代写|固体物理代写solid physics代考|The Debye model for the heat capacity
The Einstein model is correct in treating atomic vibrations as quantum oscillators, but it fails in attributing the same frequency to all of them: simply, this is inconsistent with the knowledge of the dispersion relations we developed in chapter 3. We must therefore introduce in the theory the fundamental notion that atomic oscillators can vibrate at different frequencies. Within the Debye model this notion is developed in a simplified way which allows us to carry on a clean analytical calculation of the heat capacity.
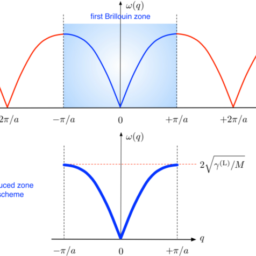
According to Debye, all phonon dispersion relations are effectively described by only three effective acoustic branches whose extension in wavevector, however, exceeds the boundary of the $1 \mathrm{BZ}$. This is shown in figure $4.2$ : the low and high $q$-values of the effective branch, respectively, describe an acoustic and an optical vibration of the real crystal. Furthermore, since for any direction there are in fact three possible phonon polarisations, the linearisation of their dispersions must properly take care to distinguish between one effective longitudinal and two effective transverse branches with slope $v_{\mathrm{g}}^{(L)}$ and $v_{\mathrm{g}}^{(T)}$, respectively (see section 3.2.1). To this aim it is useful to introduce the effective speed of sound $v_{\text {eff }}$ defined as
$$
\frac{3}{v_{\mathrm{eff}}^{3}}=\frac{1}{\left[v_{\mathrm{g}}^{(L)}\right]^{3}}+\frac{2}{\left[v_{\mathrm{g}}^{(T)}\right]^{3}}
$$
物理代写|固体物理代写SOLID PHYSICS代考|The general quantum theory for the heat capacity
Although the Debye expression for the lattice heat capacity is rather accurate over a wide range of temperatures for most materials, deviations from laboratory measurements are nevertheless found. The most effective way to develop the comparison is to fit experimental data taken at different temperatures by means of equation (4.10), while keeping $T_{\mathrm{D}}$ as the only calibration parameter for the fitting. For many systems this procedure returns a Debye temperature varying within few tens of Kelvin degrees: this is the fingerprint of some failure of the interpolation scheme, which is conceptually based on the existence of a unique Debye temperature. Good for us, these deviations are small for many practical applications and, therefore, the Debye model can be used as a very good approximation.
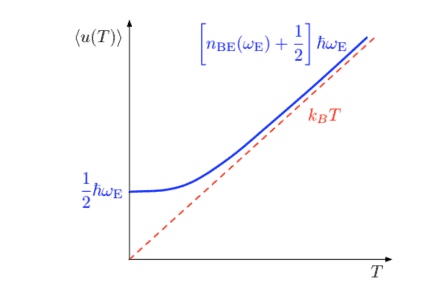
If, however, a high degree of accuracy is needed, then there is no better solution than using a full quantum theory where the lattice contribution to the internal energy $\mathcal{U}$ is calculated according to equation (3.36) so that
$$
\mathcal{U}=\mathcal{U}{0}+\sum{s \mathbf{q}}\left[n_{\mathrm{BE}}(s \mathbf{q}, T)+1 / 2\right] \hbar \omega_{s}(\mathbf{q})
$$
where $\mathcal{U}{0}$ is the total energy content of the static lattice. We accordingly calculate ${ }^{4}$ $$ \begin{aligned} \mathcal{C}{V}^{\text {quantum }}(T) &=\frac{\partial}{\partial T} \sum_{s \mathbf{q}} \frac{\hbar \omega_{s}(\mathbf{q})}{\exp \left[\hbar \omega_{s}(\mathbf{q}) / k_{\mathrm{B}} T\right]-1} \
&=\sum_{s \mathbf{q}} \hbar \omega_{s}(\mathbf{q}) \frac{\partial n_{\mathrm{BE}}(s \mathbf{q}, T)}{\partial T}=\sum_{s \mathbf{q}} \mathcal{C}{V, s \mathbf{q}}(T) \end{aligned} $$ where we used equation (3.37) for the phonon population $n{\mathrm{BE}}(s \mathbf{q}, T)$ and we introduced the specific contributions $\mathcal{C}_{V, s q}(T)$ of each $(s, \mathbf{q})$ mode to the heat capacity.
固体物理代写
物理代写|固体物理代写SOLID PHYSICS代考|HISTORICAL BACKGROUND
物理系统的能量含量在热力学上由其内部能量解释在 s和和一种pp和nd一世X$C$其对温度的导数
$$
\mathcal{C} {V}=\left.\frac{d \mathcal{U}}{d T}\right| {V},
$$
称为定容比热容在:它表示我们需要准静态提供的热量,以便将系统温度提高一度。
第一次尝试为 $\mathcal{C} {V}推导微观理论$\mathcal{C}{V}$ in crystalline solids were developed at the dawn of the XXth century. In many respects, we can consider these investigations as the beginning of quantum solid state physics [1]. Developing a microscopic theory was certainly worthy of effort since the classical theory of $\mathcal{C}{V}$ is contradicted by the experimental evidence. In order to outline this theory, outdated but still valuable for our pedagogical approach to the thermal properties, we preliminarily remark that there are three main contributions to the heat capacity of a crystal, respectively, deriving from lattice vibrations, conduction electrons, and magnetic ordering. In non-magnetic insulators the first one is by far the leading one and in this chapter we focus just on it ${ }^{1}$.
物理代写|固体物理代写SOLID PHYSICS代考|THE DEBYE MODEL FOR THE HEAT CAPACITY
爱因斯坦模型将原子振动视为量子振荡器是正确的,但它未能将相同的频率归因于所有它们:简单地说,这与我们在第 3 章中开发的色散关系的知识不一致。因此,我们必须在理论原子振荡器可以以不同频率振动的基本概念。在德拜模型中,这个概念以简化的方式发展起来,使我们能够对热容量进行干净的分析计算。
根据德拜,所有声子色散关系仅由三个有效声学分支有效地描述,但是其在波向量中的扩展超过了边界1乙从. 如图所示4.2: 低和高q有效分支的 – 值分别描述了真实晶体的声学和光学振动。此外,由于对于任何方向实际上存在三种可能的声子极化,它们色散的线性化必须适当注意区分一个有效的纵向分支和两个具有斜率的有效横向分支在G(大号)和在G(吨), 分别s和和s和C吨一世这n3.2.1. 为此目的,引入有效声速是有用的在效果 定义为
3在和FF3=1[在G(大号)]3+2[在G(吨)]3
物理代写|固体物理代写SOLID PHYSICS代考|THE GENERAL QUANTUM THEORY FOR THE HEAT CAPACITY
尽管对于大多数材料来说,晶格热容的德拜表达式在很宽的温度范围内都相当准确,但仍发现与实验室测量值存在偏差。进行比较的最有效方法是通过方程拟合在不同温度下获取的实验数据4.10, 同时保持吨D作为配件的唯一校准参数。对于许多系统,此过程返回在几十开尔文度范围内变化的德拜温度:这是插值方案某些失败的指纹,该方案在概念上基于唯一德拜温度的存在。对我们有好处,这些偏差对于许多实际应用来说很小,因此,德拜模型可以用作非常好的近似值。
然而,如果需要高精度,那么没有比使用全量子理论更好的解决方案了,其中晶格对内能的贡献在根据等式计算3.36所以
$$
\mathcal{U}=\mathcal{U}{0}+\sum{s \mathbf{q}}\left[n_{\mathrm{BE}}(s \mathbf{q}, T)+1 / 2\right] \hbar \omega_{s}(\mathbf{q})
$$
where $\mathcal{U}{0}$ is the total energy content of the static lattice. We accordingly calculate ${ }^{4}$ $$ \begin{aligned} \mathcal{C}{V}^{\text {quantum }}(T) &=\frac{\partial}{\partial T} \sum_{s \mathbf{q}} \frac{\hbar \omega_{s}(\mathbf{q})}{\exp \left[\hbar \omega_{s}(\mathbf{q}) / k_{\mathrm{B}} T\right]-1} \
&=\sum_{s \mathbf{q}} \hbar \omega_{s}(\mathbf{q}) \frac{\partial n_{\mathrm{BE}}(s \mathbf{q}, T)}{\partial T}=\sum_{s \mathbf{q}} \mathcal{C}{V, s \mathbf{q}}(T) \end{aligned} $$ where we used equation (3.37) for the phonon population $n{\mathrm{BE}}(s \mathbf{q}, T)$ and we introduced the specific contributions $\mathcal{C}_{V, s q}(T)$ of each $(s, \mathbf{q})$ 模式到热容量。

物理代写|固体物理代写solid physics代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
微观经济学代写
微观经济学是主流经济学的一个分支,研究个人和企业在做出有关稀缺资源分配的决策时的行为以及这些个人和企业之间的相互作用。my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学Mathematics代写服务。我们的专家在图论代写Graph Theory代写方面经验极为丰富,各种图论代写Graph Theory相关的作业也就用不着 说。
线性代数代写
线性代数是数学的一个分支,涉及线性方程,如:线性图,如:以及它们在向量空间和通过矩阵的表示。线性代数是几乎所有数学领域的核心。
博弈论代写
现代博弈论始于约翰-冯-诺伊曼(John von Neumann)提出的两人零和博弈中的混合策略均衡的观点及其证明。冯-诺依曼的原始证明使用了关于连续映射到紧凑凸集的布劳威尔定点定理,这成为博弈论和数学经济学的标准方法。在他的论文之后,1944年,他与奥斯卡-莫根斯特恩(Oskar Morgenstern)共同撰写了《游戏和经济行为理论》一书,该书考虑了几个参与者的合作游戏。这本书的第二版提供了预期效用的公理理论,使数理统计学家和经济学家能够处理不确定性下的决策。
微积分代写
微积分,最初被称为无穷小微积分或 “无穷小的微积分”,是对连续变化的数学研究,就像几何学是对形状的研究,而代数是对算术运算的概括研究一样。
它有两个主要分支,微分和积分;微分涉及瞬时变化率和曲线的斜率,而积分涉及数量的累积,以及曲线下或曲线之间的面积。这两个分支通过微积分的基本定理相互联系,它们利用了无限序列和无限级数收敛到一个明确定义的极限的基本概念 。
计量经济学代写
什么是计量经济学?
计量经济学是统计学和数学模型的定量应用,使用数据来发展理论或测试经济学中的现有假设,并根据历史数据预测未来趋势。它对现实世界的数据进行统计试验,然后将结果与被测试的理论进行比较和对比。
根据你是对测试现有理论感兴趣,还是对利用现有数据在这些观察的基础上提出新的假设感兴趣,计量经济学可以细分为两大类:理论和应用。那些经常从事这种实践的人通常被称为计量经济学家。
Matlab代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。