如果你也在 怎样代写金融数学Financial Mathematics这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。金融数学Financial Mathematics是将数学方法应用于金融问题。(有时使用的同等名称是定量金融、金融工程、数学金融和计算金融)。它借鉴了概率、统计、随机过程和经济理论的工具。
金融数学Financial Mathematics传统上,投资银行、商业银行、对冲基金、保险公司、公司财务部和监管机构将金融数学的方法应用于诸如衍生证券估值、投资组合结构、风险管理和情景模拟等问题。依赖商品的行业(如能源、制造业)也使用金融数学。定量分析为金融市场和投资过程带来了效率和严谨性,在监管方面也变得越来越重要。
my-assignmentexpert™金融数学Financial Mathematics代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的金融数学Financial Mathematics作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此金融数学Financial Mathematics作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学Mathematics代写服务。我们的专家在金融数学Financial Mathematics代写方面经验极为丰富,各种金融数学Financial Mathematics相关的作业也就用不着 说。
我们提供的金融数学Financial Mathematics及其相关学科的代写,服务范围广, 其中包括但不限于:
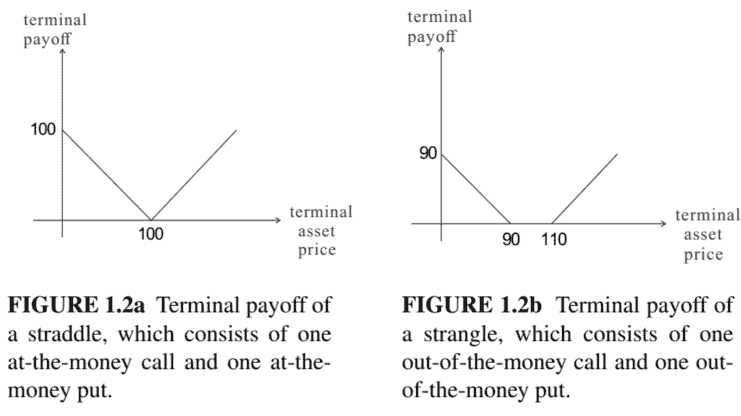
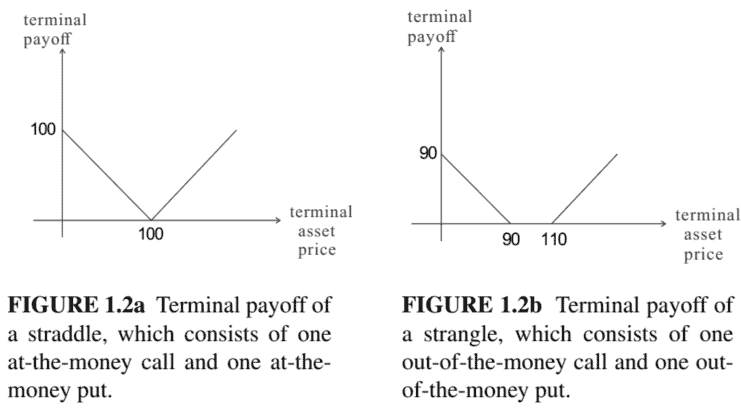
数学代写|金融数学代写Financial Mathematics代考|Taking volatility position using straddles and strangles
To benefit from an increasing volatility of the underlying asset price process in the future, one can long one at-the-money call and one at-the-money put with the same strike to form a straddle (see Fig. 1.2a). However, to establish the straddle portfolio, one has to pay the upfront premium of two expensive at-the-money options. To establish a less costly portfolio with similar volatility exposure, one may switch to a strangle which consists of one out-of-the-money put and one out-of-the-money call (see Fig. 1.2b). In order to achieve a positive terminal payoff in a strangle, the asset price has to go beyond an interval with bounds specified by the strikes of the out-ofthe-money call and put. The cost required to establish the strangle is lower when the interval becomes wider, but there is a higher chance of getting zero terminal payoff under more widened interval.
数学代写|金融数学代写Financial Mathematics代考|Volatility exposure generated by delta hedging options
Equity options provide exposure to both direction risk of the asset price and volatility risk. According to the Black-Scholes hedging principle, one can remove the exposure to the asset price risk using delta hedging. However, delta hedging can never be perfect since the real world financial markets violate many of the Black-Scholes model assumptions, like volatility cannot be accurately estimated, asset price may move discontinuously, liquidity may not be available, frequent trading would incur high transaction costs, etc.
We would like to show that delta hedging an option based on some chosen timedependent hedge volatility generates a profit and loss $(\mathrm{P} \& \mathrm{~L})$ that is related to the realized variance and the cash gamma position (defined as product of option gamma and square of asset price). Consider the underlying asset price which follows a continuous semimartingale process under a risk neutral measure $Q$ as specified by
$$
\frac{\mathrm{d} S_{t}}{S_{t}}=(r-q) \mathrm{d} t+\sigma_{t} \mathrm{~d} W_{t},
$$
where $r$ and $q$ are constant risk-free rate and dividend yield, respectively, $\sigma_{t}$ is the instantaneous volatility process, and $W_{t}$ is a standard Brownian motion under $Q$. The assumed dynamics of $S_{t}$ allows no jump. Let $\sigma_{t}^{i}$ be the time-dependent implied volatility derived from traded option prices at varying times. We write the time- $t$ option price as $V_{t}^{i}=V\left(S_{t}, t ; \sigma_{t}^{i}\right)$ with reference to implied volatility $\sigma_{t}^{i}$. Suppose an option trader sells an option at time zero priced at the current market implied volatility $\sigma_{0}^{i}$, the option price is given by $V_{0}^{i}=V\left(S_{0}, 0 ; \sigma_{0}^{i}\right)$. The seller’s short position in the option is delta hedged at some chosen time-dependent hedge volatility $\sigma_{t}^{h}$ for the remaining life of the option. In summary, for $t \in[0, T]$, there are 3 volatilities: (i) $\sigma_{t}$ is the actual instantaneous volatility of $S_{t}$, (ii) $\sigma_{t}^{i}$ is the implied volatility derived from market option price $V_{t}^{i}$ at varying time $t$, (iii) $\sigma_{t}^{h}$ is the time varying hedging volatility adopted by the hedger.
金融数学代写
数学代写|金融数学代写FINANCIAL MATHEMATICS代考|TAKING VOLATILITY POSITION USING STRADDLES AND STRANGLES
为了受益于未来标的资产价格过程的波动性增加,一个人可以做多一个平价看涨期权和一个平价看跌期权,以相同的行使价形成跨式s和和F一世G.1.2一个. 然而,要建立跨式投资组合,必须支付两个昂贵的平价期权的前期溢价。为了建立一个成本较低且具有类似波动风险的投资组合,人们可能会改用由一个价外看跌期权和一个价外看涨期权组成的扼杀式投资组合s和和F一世G.1.2b. 为了在扼杀中获得正的最终收益,资产价格必须超出一个区间,该区间由价外看涨期权和看跌期权的执行价指定。当区间变得更宽时,建立扼杀所需的成本较低,但在更宽的区间下获得零终端收益的机会更高。
数学代写|金融数学代写FINANCIAL MATHEMATICS代考|VOLATILITY EXPOSURE GENERATED BY DELTA HEDGING OPTIONS
股票期权提供资产价格方向风险和波动风险的敞口。根据 Black-Scholes 对冲原理,可以使用 delta 对冲消除资产价格风险敞口。然而,delta对冲永远不会是完美的,因为现实世界的金融市场违反了许多Black-Scholes模型假设,比如波动性无法准确估计,资产价格可能不连续波动,流动性可能不可用,频繁交易会产生高额交易成本, ETC。
我们想证明,基于某些选择的时间相关对冲波动率对期权进行 delta 对冲会产生损益(磷& 大号)这与已实现的方差和现金伽玛头寸有关d和F一世n和d一个spr○d在C吨○F○p吨一世○nG一个米米一个一个ndsq在一个r和○F一个ss和吨pr一世C和. 考虑在风险中性测度下遵循连续半鞅过程的标的资产价格问如指定的
$$
\frac{\mathrm{d} S_{t}}{S_{t}}=(r-q) \mathrm{d} t+\sigma_{t} \mathrm{~d} W_{t},
$$
在哪里r和q分别是恒定的无风险利率和股息收益率,σ吨是瞬时波动过程,并且在吨是一个标准的布朗运动问. 假设的动力学小号吨不允许跳跃。让σ吨一世是从不同时间的交易期权价格得出的与时间相关的隐含波动率。我们写下时间——吨期权价格为在吨一世=在(小号吨,吨;σ吨一世)参考隐含波动率σ吨一世. 假设期权交易者在零时间以当前市场隐含波动率卖出期权σ0一世, 期权价格由下式给出在0一世=在(小号0,0;σ0一世). 卖方在期权中的空头头寸以某些选定的时间相关对冲波动率进行 delta 对冲σ吨H为期权的剩余寿命。总之,对于吨∈[0,吨],有3个波动率:一世 σ吨是实际的瞬时波动率小号吨, 一世一世 σ吨一世是从市场期权价格推导出的隐含波动率在吨一世在不同的时间吨,一世一世一世 σ吨H是套期保值者采用的时变套期保值波动率。

数学代写|金融数学代写Financial Mathematics代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
微观经济学代写
微观经济学是主流经济学的一个分支,研究个人和企业在做出有关稀缺资源分配的决策时的行为以及这些个人和企业之间的相互作用。my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学Mathematics代写服务。我们的专家在图论代写Graph Theory代写方面经验极为丰富,各种图论代写Graph Theory相关的作业也就用不着 说。
线性代数代写
线性代数是数学的一个分支,涉及线性方程,如:线性图,如:以及它们在向量空间和通过矩阵的表示。线性代数是几乎所有数学领域的核心。
博弈论代写
现代博弈论始于约翰-冯-诺伊曼(John von Neumann)提出的两人零和博弈中的混合策略均衡的观点及其证明。冯-诺依曼的原始证明使用了关于连续映射到紧凑凸集的布劳威尔定点定理,这成为博弈论和数学经济学的标准方法。在他的论文之后,1944年,他与奥斯卡-莫根斯特恩(Oskar Morgenstern)共同撰写了《游戏和经济行为理论》一书,该书考虑了几个参与者的合作游戏。这本书的第二版提供了预期效用的公理理论,使数理统计学家和经济学家能够处理不确定性下的决策。
微积分代写
微积分,最初被称为无穷小微积分或 “无穷小的微积分”,是对连续变化的数学研究,就像几何学是对形状的研究,而代数是对算术运算的概括研究一样。
它有两个主要分支,微分和积分;微分涉及瞬时变化率和曲线的斜率,而积分涉及数量的累积,以及曲线下或曲线之间的面积。这两个分支通过微积分的基本定理相互联系,它们利用了无限序列和无限级数收敛到一个明确定义的极限的基本概念 。
计量经济学代写
什么是计量经济学?
计量经济学是统计学和数学模型的定量应用,使用数据来发展理论或测试经济学中的现有假设,并根据历史数据预测未来趋势。它对现实世界的数据进行统计试验,然后将结果与被测试的理论进行比较和对比。
根据你是对测试现有理论感兴趣,还是对利用现有数据在这些观察的基础上提出新的假设感兴趣,计量经济学可以细分为两大类:理论和应用。那些经常从事这种实践的人通常被称为计量经济学家。
Matlab代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。