如果你也在 怎样代写统计力学Statistical Mechanics这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。统计力学Statistical Mechanics在物理学中,是一个数学框架,它将统计方法和概率理论应用于大型微观实体的集合。它不假设或假定任何自然法则,而是从这些集合体的行为来解释自然界的宏观行为。
统计力学Statistical Mechanics产生于经典热力学的发展,对该领域而言,它成功地解释了宏观物理特性–如温度、压力和热容量–以围绕平均值波动的微观参数和概率分布为特征。这建立了统计热力学和统计物理学的领域。
my-assignmentexpert™统计力学Statistical Mechanics代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的统计力学Statistical Mechanics作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此统计力学Statistical Mechanics作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在物理Physical代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的物理Physical代写服务。我们的专家在统计力学Statistical Mechanics代写方面经验极为丰富,各种统计力学Statistical Mechanics相关的作业也就用不着 说。
我们提供的统计力学Statistical Mechanics及其相关学科的代写,服务范围广, 其中包括但不限于:

物理代写|统计力学代写Statistical Mechanics代写|Objections from Loschmidt and Zermelo
At the time of Boltzmann there were two kind of objections raised against his scheme: one due to the Austrian physico-chemist Josef Loschmidt (1821-1895) and another one due to the German mathematician Ernst Zermelo (1871-1953). ${ }^{4}$
The objection of Loschmidt” 232 which was based on the reversibility “paradox” was answered in detail in Sect. 8.1.3. The objection of Zermelo was based on Poincaré’s recurrence theorem . ${ }^{6}$ This theorem implies that, if all the particles of a gas start in a half-box, they must return, all at the same time, to the half-box that they started from “if we wait long enough.”
Boltzmann’s answer was simple and based on the end of the previous sentence: “you should live that long”! $!^{7}$
Even elementary estimates of the time it takes for such Poincaré’s recurrence to occur is easily seen to be much larger than the age of the universe. In footnote 4.3, we made a rough estimate of these times: assuming that the dynamics of the gas is ergodic , the time spent between two consecutive visits to the region in phase space where all the particles are in a half-box is of the order of $2^{10^{23}}$, which is much larger than the age of the universe the units of time, seconds or hours, do not matter much for this conclusion to hold, as long as they are reasonable.
物理代写|统计力学代写Statistical Mechanics代写|An Objection from Poincaré
There was another objection, a rather strange one, due again to the great French mathematician Henri Poincaré. As we saw in the last subsection, he did share Loschmidt’s and Zermelo’s objections to Boltzmann, but in 1889 he came up with another objection [260].
He proved that there is no function of the positions and momenta of an isolated dynamical system that increases monotonically towards a maximum, hence there cannot be an entropy function satisfying Boltzmann’s requirements for such a function.
The details of Poincaré’s argument need not concern us, since his fundamental misconception is that he identifies this purported maximum of the entropy function with a mechanical equilibrium of the mechanical system, i.e. a point of phase space where the velocities vanish and the potential function reaches a stationary value (where $\nabla_{\vec{q}_{i}} V(\mathbf{q})=0, \forall i=1, \ldots, N$ and therefore, by (3.2.6), the particles are at rest).
But it is enough to consider a gas “in equilibrium” in the sense of Boltzmann to realize that this has nothing to do with a mechanical equilibrium: far from being at rest, particles bounce back and forth between the walls of the box. Moreover, thermodynamic equilibrium corresponds to a set of configurations, not to a single one.
Of course it is true that Boltzmann’s entropy, as a function of the microstate, does not always increase, partly because of Poincaré’s recurrences, partly because of exceptional initial conditions. But one did not need Poincaré’s argument to know that.
It is not clear what Poincaré had in mind when trying to prove this “impossibility result” but it illustrate the lack of understanding that sometimes exists between physicists and mathematicians, even the greatest ones.
物理代写|统计力学代写Statistical Mechanics代写|Objections to Typicality Arguments
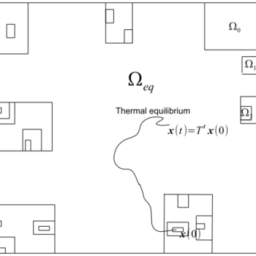
Consider any given microscopic trajectory $T^{t} \mathbf{x}{0}$ of a physical system and consider its complement $\Omega \backslash\left{T^{t} \mathbf{x}{0} \mid t \in \mathbb{R}\right}$ on the phase space $\Omega$ or on a given energy surface $S_{E} \backslash\left{T^{t} \mathbf{x}{0} \mid t \in \mathbb{R}\right}$. Obviously, with respect to any reasonable measure which is not concentrated on that trajectory, the set $\left{T^{t} \mathbf{x}{0} \mid t \in \mathbb{R}\right}$ is of measure 0 and thus, from our definition, its complement is typical. Yet, by definition, the trajectory does not enter that complement; hence, concludes the objection, the fact that a set of configurations is typical does not mean that a trajectory goes into it.
More generally, any argument that is supposed to apply to all trajectories except those in a set of small measure or even of measure zero can be “refuted” by pointing out that any given trajectory is such a set of measure zero.
统计力学代写
物理代写|统计力学代写STATISTICAL MECHANICS代写|OBJECTIONS FROM LOSCHMIDT AND ZERMELO
在玻尔兹曼时代,有人对他的计划提出了两种反对意见:一种是由于奥地利物理化学家约瑟夫·洛施密特(Josef Loschmidt)1821−1895另一个归功于德国数学家 Ernst Zermelo1871−1953. 4
Loschmidt” 232 基于可逆性“悖论”的反对意见在 Sect. 8.1.3. 策梅洛的反对是基于庞加莱的递归定理。6这个定理意味着,如果气体的所有粒子都从一个半盒子开始,那么它们必须同时返回到它们从“如果我们等待足够长的时间”开始的半盒子。
玻尔兹曼的回答很简单,基于上一句的结尾:“你应该活那么久”!!7
即使是对这种庞加莱重复发生所需时间的初步估计,也很容易看出比宇宙的年龄要大得多。在脚注 4.3 中,我们对这些时间进行了粗略估计:假设气体的动力学是遍历的,那么两次连续访问相空间中所有粒子都在半盒中的区域之间花费的时间是顺序的的21023,它比宇宙的年龄大得多的时间单位,秒或小时,只要它们是合理的,这个结论的成立并不重要。
物理代写|统计力学代写STATISTICAL MECHANICS代写|AN OBJECTION FROM POINCARÉ
还有另一个反对意见,一个相当奇怪的反对意见,同样来自伟大的法国数学家亨利庞加莱。正如我们在上一小节中看到的,他确实同意洛施密特和策梅洛对玻尔兹曼的反对意见,但在 1889 年他提出了另一个反对意见260.
他证明了孤立动力系统的位置和动量不存在单调向最大值增加的函数,因此不可能存在满足玻尔兹曼对这样一个函数的要求的熵函数。
Poincaré 论证的细节不必关心我们,因为他的基本误解是他将熵函数的这个所谓的最大值与机械系统的机械平衡相结合,即速度消失且势函数达到的相空间点固定值在H和r和$∇q→一世在(q=0, \forall i=1, \ldots, N$ 因此,由3.2.6,粒子处于静止状态)。
但是考虑玻尔兹曼意义上的“平衡”气体就足以认识到这与机械平衡无关:粒子远非静止,而是在盒子的壁之间来回反弹。此外,热力学平衡对应于一组配置s和和F一世G.6.2,而不是一个。
当然,玻尔兹曼的熵作为微观状态的函数并不总是增加,这是真的,部分原因是庞加莱的递归,部分原因是特殊的初始条件。但人们不需要庞加莱的论证就知道这一点。
目前尚不清楚庞加莱在试图证明这种“不可能的结果”时的想法,但它说明了物理学家和数学家之间有时存在的缺乏理解,即使是最伟大的人。
物理代写|统计力学代写STATISTICAL MECHANICS代写|OBJECTIONS TO TYPICALITY ARGUMENTS
考虑任何给定的微观轨迹$T^{t} \$mathbf{x}{0}$的物理系统,并考虑它的补充$Omega\backslash\left{T^{t}}。\mathbf{x}{0}。\mid t\in mathbb{R}\right}$在相空间$Omega$或在给定的能量表面$S_{E}上。\backslash\left{T^{t}}。\σbf{x}{0}。\mid t\inmathbb{R}\right}$。显然,就任何不集中于该轨迹的合理度量而言,集合$left{T^{t} \mathbf{x}{0}}。\mid t\in `mathbb{R}\right}$的度量是0,因此,从我们的定义来看,它的补集是典型的。然而,根据定义,轨迹并不进入该补集;因此,反对意见的结论是,一组配置是典型的这一事实并不意味着轨迹会进入其中。
更一般地说,任何应该适用于所有轨迹的论点,除了在一组小度量甚至零度量中的那些轨迹,都可以通过指出任何给定的轨迹都是这样的一组零度量来“反驳”。

物理代写|统计力学代写Statistical Mechanics代写 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
微观经济学代写
微观经济学是主流经济学的一个分支,研究个人和企业在做出有关稀缺资源分配的决策时的行为以及这些个人和企业之间的相互作用。my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学Mathematics代写服务。我们的专家在图论代写Graph Theory代写方面经验极为丰富,各种图论代写Graph Theory相关的作业也就用不着 说。
线性代数代写
线性代数是数学的一个分支,涉及线性方程,如:线性图,如:以及它们在向量空间和通过矩阵的表示。线性代数是几乎所有数学领域的核心。
博弈论代写
现代博弈论始于约翰-冯-诺伊曼(John von Neumann)提出的两人零和博弈中的混合策略均衡的观点及其证明。冯-诺依曼的原始证明使用了关于连续映射到紧凑凸集的布劳威尔定点定理,这成为博弈论和数学经济学的标准方法。在他的论文之后,1944年,他与奥斯卡-莫根斯特恩(Oskar Morgenstern)共同撰写了《游戏和经济行为理论》一书,该书考虑了几个参与者的合作游戏。这本书的第二版提供了预期效用的公理理论,使数理统计学家和经济学家能够处理不确定性下的决策。
微积分代写
微积分,最初被称为无穷小微积分或 “无穷小的微积分”,是对连续变化的数学研究,就像几何学是对形状的研究,而代数是对算术运算的概括研究一样。
它有两个主要分支,微分和积分;微分涉及瞬时变化率和曲线的斜率,而积分涉及数量的累积,以及曲线下或曲线之间的面积。这两个分支通过微积分的基本定理相互联系,它们利用了无限序列和无限级数收敛到一个明确定义的极限的基本概念 。
计量经济学代写
什么是计量经济学?
计量经济学是统计学和数学模型的定量应用,使用数据来发展理论或测试经济学中的现有假设,并根据历史数据预测未来趋势。它对现实世界的数据进行统计试验,然后将结果与被测试的理论进行比较和对比。
根据你是对测试现有理论感兴趣,还是对利用现有数据在这些观察的基础上提出新的假设感兴趣,计量经济学可以细分为两大类:理论和应用。那些经常从事这种实践的人通常被称为计量经济学家。
Matlab代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。