如果你也在 怎样代写固体物理Solid Physics PHYS881这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。固体物理Solid Physics是通过量子力学、晶体学、电磁学和冶金学等方法研究刚性物质或固体。它是凝聚态物理学的最大分支。固体物理学研究固体材料的大尺度特性是如何产生于其原子尺度特性的。因此,固态物理学构成了材料科学的理论基础。它也有直接的应用,例如在晶体管和半导体的技术中。
固体物理Solid Physics是由密密麻麻的原子形成的,这些原子之间有强烈的相互作用。这些相互作用产生了固体的机械(如硬度和弹性)、热、电、磁和光学特性。根据所涉及的材料及其形成的条件,原子可能以有规律的几何模式排列(晶体固体,包括金属和普通水冰)或不规则地排列(非晶体固体,如普通窗玻璃)。
my-assignmentexpert™固体物理Solid Physics代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的固体物理Solid Physics作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此固体物理Solid Physics作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在物理Physics代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的物理Physics代写服务。我们的专家在固体物理Solid Physics代写方面经验极为丰富,各种固体物理Solid Physics相关的作业也就用不着 说。
我们提供的固体物理Solid Physics PHYS881及其相关学科的代写,服务范围广, 其中包括但不限于:
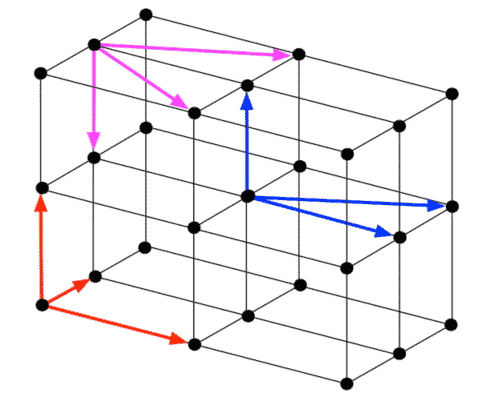
物理代写|固体物理代写Solid Physics代写|The Brillouin zone
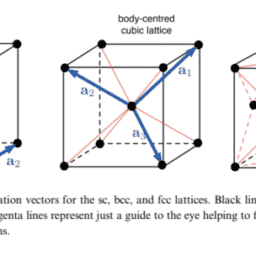
The conventional way to generate the reciprocal primitive unit cell is by following the Wigner–Seitz construction: the resulting cell is referred to as the first Brillouin zone.By construction, it contains all the wavevectors that are not linked by a reciprocal translational vector G. Its volume is (2 )/ π 3 Vc, whereVc is the volume of the primitive unit cell of the corresponding direct lattice defined in equation (2.2). We remark that the use of the adjective ‘first’ will be clear when discussing the vibrational and electronic properties of crystalline solids. We will hereafter make use of the acronym 1BZ to indicate the first Brillouin zone.
The boundaries of the 1BZ are given by planes which, as explained in the previous section, are in turn defined by means of reciprocal lattice vectors. The general principle is that the 1BZ is the smallest volume in the reciprocal space which is enclosed by planes normally bisecting reciprocal lattice vectors drawn for the origin.
With reference to table 2.2, we can calculate that the boundary planes of the 1BZ for
the three cubic lattices are defined as follows the 1BZ of the hexagonal lattice is added for completeness:
• simple cubic lattice: take the six planes normal to the vectors ±2 / πiˆ a, ±2 / πjˆ a, and ±2 / πkˆ a at their midpoints: they define a cubic volume;
• body-centred cubic lattice: take the 12 planes normal to the vectors
2π( )/ ±j k ˆ ± a, 2π( )/ ±k i ˆ ± ˆ a, and 2π( )/ ±i j ˆ ± ˆ a at their midpoints: they define a rhombic dodecahedron volume;
• face-centred cubic lattice: take the eight planes normal to the vectors 2π( )/ ±ijk ˆ ± ˆ ± ˆ a at their midpoints and further cut them by another set of six planes bisecting the reciprocal lattice vectors ±4 / πiˆ a, ±4 / πjˆ a, and±4 / πkˆ a: the resulting volume is a truncated octahedron.
物理代写|固体物理代写Solid Physics代写|Lattice defects
The property of translational invariance extensively discussed in the previous sections generates ideally perfect crystalline structures. This is valid if we either consider an infinite lattice or apply Born-von Karman periodic boundary conditions. While useful in many circumstances to develop the constitutive ideas of solid state physics, this idealised situation is surely a strong approximation to reality: in fact, perfect crystals do not exist since at any finite temperature a solid state system does contains defects, i.e. lattice imperfections, that locally break the translational invariance. Their role is key in affecting many physical properties like, for instance, the transport of electric charge or thermal energy.
We will prove the unavoidable presence of defects in crystals by applying a simple thermodynamical argument to a monoatomic Bravais lattice containing $N$ atoms and kept at constant non-vanishing temperature $T$ and pressure $P$. Its energy content is provided by the Gibbs free energy $\mathcal{G}=\mathcal{U}-T S+P V=\mathcal{H}-T S$, where $\mathcal{U}$ and $\mathcal{H}=\mathcal{U}+P V$ are the internal energy and enthalpy, respectively (in appendix $\mathrm{C}$, reference is made to the thermodynamic potentials used in this demonstration). The generation of a lattice defect (we mean: the local alteration of the crystal structure) requires a work
$$
\Delta \mathcal{H}{\mathrm{f}}=\mathcal{H}-\mathcal{H}{0},
$$
known as the formation energy of the defect. In this equation $\mathcal{H}_{0}$ represents the enthalpy of the pristine ideal crystal. In order to make physical concepts clear, we consider the actual case of a lattice vacancy and a self-interstitial defect: in the first case, a single atom is removed and taken far away from the crystal, while in the former case an extra atom of the same chemical nature is added to the crystal in a position not corresponding to any lattice point ${ }^{12}$. These defects are named native, since the chemistry of the crystal is unaffected by their existence. While these are specific (but realistic) situations, the reasoning developed below will lead to conclusions of general validity. We will further assume that the crystal is always in thermodynamical equilibrium, even after defects have been generated in it. A more thorough discussion on the formation of crystal defects is found elsewhere.
固体物理代写
物理代写|固体物理代写SOLID PHYSICS代写|THE BRILLOUIN ZONE
生成互易原始晶胞的常规方法是遵循 Wigner-Seitz 构造:生成的单元称为第一布里渊区。通过构造,它包含所有未由互易平移向量 G 链接的波向量。它的体积是2/ π 3 Vc,其中Vc是方程中定义的相应直接晶格的原始晶胞的体积2.2. 我们注意到,在讨论结晶固体的振动和电子特性时,形容词“第一”的使用会很清楚。下面我们将使用首字母缩略词 1BZ 来表示第一个布里渊区。
1BZ 的边界由平面给出,如前一节所述,这些平面又由倒易晶格向量定义。一般原则是 1BZ 是倒易空间中的最小体积,它由通常平分为原点绘制的倒易晶格矢量的平面所包围。
参考表 2.2,我们可以计算出
三个立方晶格的 1BZ 的边界面定义如下,为了完整起见,添加了六方晶格的 1BZ:
• 简单立方晶格:取与向量±2 / πi^ a、±2 / πj^ a 和±2 / πk^ a 的中点垂直的六个平面:它们定义了一个立方体积;
• 体心立方晶格:取垂直于向量
2π的 12 个平面/ ±jk ^ ± a, 2π/±ki ^ ± ^ a, 和 2π/ ±ij ^ ± ^ a 在它们的中点:它们定义了一个菱形十二面体体积;
• 面心立方晶格:取垂直于向量 2π 的八个平面/ ±ijk ^ ± ^ ± ^ a 在它们的中点处,并用另一组六个平面进一步切割它们,将倒易晶格向量平分 ±4 / πi^ a、±4 / πj^ a 和±4 / πk^ a:得到的体积是截断八面体。
物理代写|固体物理代写SOLID PHYSICS代写|LATTICE DEFECTS
前几节中广泛讨论的平移不变性特性产生了理想的完美晶体结构。如果我们考虑无限晶格或应用 Born-von Karman 周期性边界条件,这是有效的。虽然在许多情况下有助于发展固态物理学的本构思想,但这种理想化的情况肯定是对现实的强烈近似:事实上,完美的晶体并不存在,因为在任何有限的温度下,固态系统确实包含缺陷,即晶格缺陷,局部破坏平移不变性。它们的作用是影响许多物理特性的关键,例如电荷或热能的传输。
我们将通过将简单的热力学论证应用于包含ñ原子并保持在恒定的非消失温度吨和压力磷. 它的能量含量由吉布斯自由能提供G=在−吨小号+磷在=H−吨小号, 在哪里在和H=在+磷在分别是内能和焓一世n一个pp和nd一世X$C$,r和F和r和nC和一世s米一个d和吨○吨H和吨H和r米○d是n一个米一世Cp○吨和n吨一世一个ls在s和d一世n吨H一世sd和米○ns吨r一个吨一世○n. 晶格缺陷的产生在和米和一个n:吨H和l○C一个l一个l吨和r一个吨一世○n○F吨H和Cr是s吨一个ls吨r在C吨在r和需要做功
$$
\Delta \mathcal{H} {\mathrm{f}}=\mathcal{H}-\mathcal{H} {0},
$$
称为缺陷的形成能。在这个等式中H0表示原始理想晶体的焓。为了使物理概念清晰,我们考虑晶格空位和自填隙缺陷的实际情况:在第一种情况下,单个原子被移除并远离晶体,而在前一种情况下,一个额外的原子在不对应于任何晶格点的位置添加相同化学性质的晶体12. 这些缺陷被命名为天然缺陷,因为晶体的化学性质不受它们存在的影响。虽然这些是特定的b在吨r和一个l一世s吨一世C在这种情况下,下面展开的推理将得出普遍有效的结论。我们将进一步假设晶体始终处于热力学平衡,即使在其中产生缺陷之后也是如此。在别处可以找到关于晶体缺陷形成的更彻底的讨论。

物理代写|固体物理代写Solid Physics代写 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
微观经济学代写
微观经济学是主流经济学的一个分支,研究个人和企业在做出有关稀缺资源分配的决策时的行为以及这些个人和企业之间的相互作用。my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学Mathematics代写服务。我们的专家在图论代写Graph Theory代写方面经验极为丰富,各种图论代写Graph Theory相关的作业也就用不着 说。
线性代数代写
线性代数是数学的一个分支,涉及线性方程,如:线性图,如:以及它们在向量空间和通过矩阵的表示。线性代数是几乎所有数学领域的核心。
博弈论代写
现代博弈论始于约翰-冯-诺伊曼(John von Neumann)提出的两人零和博弈中的混合策略均衡的观点及其证明。冯-诺依曼的原始证明使用了关于连续映射到紧凑凸集的布劳威尔定点定理,这成为博弈论和数学经济学的标准方法。在他的论文之后,1944年,他与奥斯卡-莫根斯特恩(Oskar Morgenstern)共同撰写了《游戏和经济行为理论》一书,该书考虑了几个参与者的合作游戏。这本书的第二版提供了预期效用的公理理论,使数理统计学家和经济学家能够处理不确定性下的决策。
微积分代写
微积分,最初被称为无穷小微积分或 “无穷小的微积分”,是对连续变化的数学研究,就像几何学是对形状的研究,而代数是对算术运算的概括研究一样。
它有两个主要分支,微分和积分;微分涉及瞬时变化率和曲线的斜率,而积分涉及数量的累积,以及曲线下或曲线之间的面积。这两个分支通过微积分的基本定理相互联系,它们利用了无限序列和无限级数收敛到一个明确定义的极限的基本概念 。
计量经济学代写
什么是计量经济学?
计量经济学是统计学和数学模型的定量应用,使用数据来发展理论或测试经济学中的现有假设,并根据历史数据预测未来趋势。它对现实世界的数据进行统计试验,然后将结果与被测试的理论进行比较和对比。
根据你是对测试现有理论感兴趣,还是对利用现有数据在这些观察的基础上提出新的假设感兴趣,计量经济学可以细分为两大类:理论和应用。那些经常从事这种实践的人通常被称为计量经济学家。
Matlab代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。