如果你也在 怎样代写非参数统计Nonparametric Statistics BIOSTAT885这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。非参数统计Nonparametric Statistics是指的是一种统计方法,其中不假设数据来自于由少量参数决定的规定模型;这种模型的例子包括正态分布模型和线性回归模型。非参数统计有时使用的数据是顺序性的,这意味着它不依赖于数字,而是依赖于排序或排序的方式。例如,传达消费者从喜欢到不喜欢的偏好的调查将被认为是序数数据。
非参数统计Nonparametric Statistics包括非参数描述性统计、统计模型、推理和统计检验。非参数模型的模型结构不是先验的,而是由数据决定的。术语非参数化并不意味着这类模型完全没有参数,而是意味着参数的数量和性质是灵活的,不是事先固定的。直方图是概率分布的非参数估计的一个例子。
非参数统计Nonparametric Statistics代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。 最高质量的非参数统计Nonparametric Statistics作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此非参数统计Nonparametric Statistics作业代写的价格不固定。通常在专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
同学们在留学期间,都对各式各样的作业考试很是头疼,如果你无从下手,不如考虑my-assignmentexpert™!
my-assignmentexpert™提供最专业的一站式服务:Essay代写,Dissertation代写,Assignment代写,Paper代写,Proposal代写,Proposal代写,Literature Review代写,Online Course,Exam代考等等。my-assignmentexpert™专注为留学生提供Essay代写服务,拥有各个专业的博硕教师团队帮您代写,免费修改及辅导,保证成果完成的效率和质量。同时有多家检测平台帐号,包括Turnitin高级账户,检测论文不会留痕,写好后检测修改,放心可靠,经得起任何考验!
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
我们在统计Statistics代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的统计Statistics代写服务。我们的专家在多元统计分析Multivariate Statistical Analysis代写方面经验极为丰富,各种多元统计分析Multivariate Statistical Analysis相关的作业也就用不着 说。
统计代写|非参数统计代写Nonparametric Statistics代考|Using the Estimator Sp
Next, we illustrate the probability limits based Shewhart $S$ chart with $S_{p}$ as the estimator of $\sigma$. Note that, for this data set, the Phase I estimator $S_{p}=$ $\sqrt{\sum_{i=1}^{m} S_{i}^{2} / m}=0.1391$. From Table $\mathrm{H}$ in Appendix A, the needed charting constants are found to be $H_{3}^{}(25,5)=0.1581$ and $H_{4}^{}(25,5)=2.1240$ for a nominal $A R L_{\mathrm{IC}}=370$. Thus, the probability limits-based Shewhart $S$ chart is given by $L C L=H_{3}^{}(m, n) S_{p}=(0.1581)(0.1391)=0.0220$ and $U C L=H_{4}^{}(m, n) S_{p}=(2.1240)(0.1391)=0.2955$ with $C L=0.1391$. Note that this chart is slightly narrower than the probability limits-based Shewhart $S$ chart using the estimator $\bar{S} / c_{4}$ shown in Figure 3.26. This is expected since $S_{p}$ is a more efficient estimator than $\bar{S} / c_{4}$.
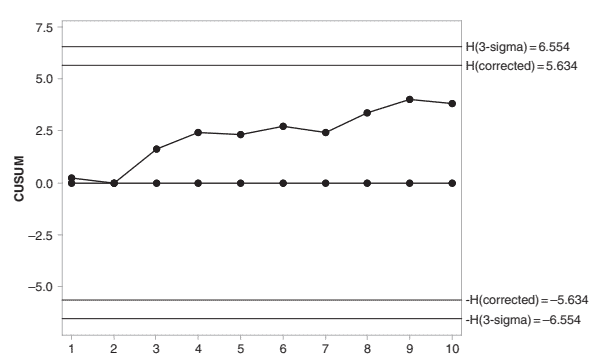
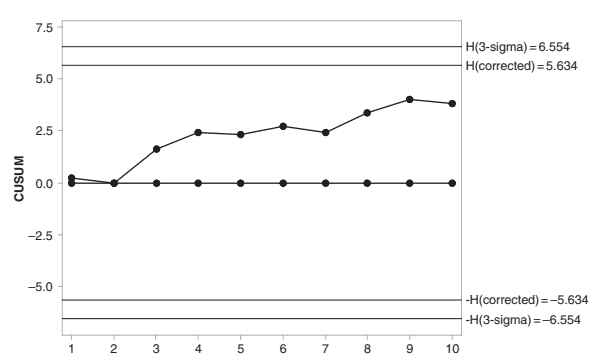
In Figure 3.27, all of the points plot between the control limits and there are no anomalous patterns in the data. Hence, we conclude that the process is functioning in statistical control with respect to variation.
统计代写|非参数统计代写Nonparametric Statistics代考|The Shewhart Chart for the Mean in Case U
The conditioning-unconditioning (CUC) method, which was first explicitly coined and used in Chakraborti (2000), is explained here for the parametric Shewhart $\bar{X}$ control chart for the mean, assuming the normal distribution. This development is important since the “standards unknown” case, that is, Case $\mathrm{U}$, is the situation often encountered in practice, and the Shewhart $\bar{X}$ control chart for the mean is one of the most popular charts used in practice. A brief background is given before going into detail. Recall that in the “standards known” case, that is, when process parameters are known (or Case $\mathrm{K}$ ), the signaling events are mutually independent so that the run-length distribution is geometric with the probability of a success (which, in $\mathrm{SPC}$, is a signal) equal to, say, some $\theta$. This result completely characterizes the performance of the Shewhart control chart in Case $K$, so that all performance properties of the chart can be obtained from the properties of the $G E O(\theta)$ distribution. Thus, the expected value of the run-length distribution is the reciprocal of $\theta$. For the IC run-length distribution, the $A R L_{\mathrm{IC}}$, simply equals the reciprocal of the $F A R$, which is the probability of a signal $\theta$ when the process is IC. The IC signal probability is denoted by $\alpha$ and therefore, $A R L_{\mathrm{TC}}=1 / \alpha$ so that specifying the $F A R$ specifies the $A R L_{\mathrm{TC}}$ and vice versa. This simple relationship makes understanding the performance of the Shewhart $\bar{X}$ chart easier in Case $\mathrm{K}$. Conversely, when the process parameters are unknown and need to be estimated to set up the control limits before Phase II process monitoring can begin, the signaling events are no longer independent so that the run-length distribution is no longer geometric. As a consequence, for example, the $A R L$ is no longer the reciprocal of the probability of a signal. This is the fundamental conceptual difference between Case $\mathrm{K}$ and Case U, which has important implications since some may find it tempting to use the results of Case $\mathrm{K}$ to design control charts even when the underlying process parameters are unknown. Practitioners are cautioned against this (see, for example, Quesenberry, 1993) practice and we thus discuss how to handle the situation properly. To this end, we use an important tool called the “conditioning-unconditioning method” proposed in Chakraborti (2000) and used extensively in the literature by many researchers. Note that Chen (1997), among others, has also used similar ideas.
非参数统计代写
统计代写|非参数统计代写NONPARAMETRIC STATISTICS代 考|USING THE ESTIMATOR SP
中,发现所需的制图営数为 $H_{3}(25,5)=0.1581$ 和 $H_{4}(25,5)=2.1240$ 对于名义上 $A R L_{\mathrm{IC}}=370$. 因此,基于概率极限的 Shewhart $S$ 图表由
$L C L=H_{3}(m, n) S_{p}=(0.1581)(0.1391)=0.0220$ 和 $U C L=H_{4}(m, n) S_{p}=(2.1240)(0.1391)=0.2955$ 和 $C L=0.1391$. 请注意,此图表比基于概率限生
在图 3.27中,所有点都绘制在控制限之间,并且数据中没有异常模式。因此,我们得出结论,该过程在关于变异的统计控制中起作用。
统计代写|非参数统计代写NONPARAMETRIC STATISTICS代考|THE SHEWHART CHART FOR THE MEAN IN CASE U
末知”安例,即安例U, 是实践中经常遇到的情况,而 Shewhart $\bar{X}$ 均值控制图是实践中最流行的图表之一。在详细介绍之前先简要介绍一下氺暠。佃回想一下,在“标
准已知”的情况下,即工艺参数已知时orCase $\$ \mathrm{~K} \$$ ,信令事件是相互独立的,因此游程分布是几何的,具有成功的概率which, in $\$ \mathrm{SPC} \$$, isasignal等于,比如
说,一些 $\theta$. 该结果完全表征了 Case 中 Shewhart控制图的性能 $K$, 这样图表的所有性能属性都可以从 $G E O(\theta)$ 分配。 因此,游程分布的期望值是 $\theta$. 对于 IC 游程长度
因此运行长度分布不再是几何分布。因此,例如, $A R L$ 不再是信号概率的倒数。这是 Case之间的基本概念区别 $\mathrm{K}$ 和䒺例 U,它具有重要意义,因为有些人可能会

统计代写|非参数统计代写Nonparametric Statistics代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
微观经济学代写
微观经济学是主流经济学的一个分支,研究个人和企业在做出有关稀缺资源分配的决策时的行为以及这些个人和企业之间的相互作用。my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学Mathematics代写服务。我们的专家在图论代写Graph Theory代写方面经验极为丰富,各种图论代写Graph Theory相关的作业也就用不着 说。
线性代数代写
线性代数是数学的一个分支,涉及线性方程,如:线性图,如:以及它们在向量空间和通过矩阵的表示。线性代数是几乎所有数学领域的核心。
博弈论代写
现代博弈论始于约翰-冯-诺伊曼(John von Neumann)提出的两人零和博弈中的混合策略均衡的观点及其证明。冯-诺依曼的原始证明使用了关于连续映射到紧凑凸集的布劳威尔定点定理,这成为博弈论和数学经济学的标准方法。在他的论文之后,1944年,他与奥斯卡-莫根斯特恩(Oskar Morgenstern)共同撰写了《游戏和经济行为理论》一书,该书考虑了几个参与者的合作游戏。这本书的第二版提供了预期效用的公理理论,使数理统计学家和经济学家能够处理不确定性下的决策。
微积分代写
微积分,最初被称为无穷小微积分或 “无穷小的微积分”,是对连续变化的数学研究,就像几何学是对形状的研究,而代数是对算术运算的概括研究一样。
它有两个主要分支,微分和积分;微分涉及瞬时变化率和曲线的斜率,而积分涉及数量的累积,以及曲线下或曲线之间的面积。这两个分支通过微积分的基本定理相互联系,它们利用了无限序列和无限级数收敛到一个明确定义的极限的基本概念 。
计量经济学代写
什么是计量经济学?
计量经济学是统计学和数学模型的定量应用,使用数据来发展理论或测试经济学中的现有假设,并根据历史数据预测未来趋势。它对现实世界的数据进行统计试验,然后将结果与被测试的理论进行比较和对比。
根据你是对测试现有理论感兴趣,还是对利用现有数据在这些观察的基础上提出新的假设感兴趣,计量经济学可以细分为两大类:理论和应用。那些经常从事这种实践的人通常被称为计量经济学家。
Matlab代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。