如果你也在 怎样代写空气动力学Aerodynamics ME615这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。空气动力学Aerodynamics可以追溯到十七世纪,但空气动力已经被人类利用在帆船和风车上达数千年之久,飞行的图像和故事也出现在有记载的历史中,如古希腊的伊卡洛斯和代达罗斯的传说。连续体、阻力和压力梯度的基本概念出现在亚里士多德和阿基米德的著作中。
空气动力学Aerodynamics源于古希腊语:aero(空气)+古希腊语:δυναμική(动力学),是对空气运动的研究,特别是当受到固体物体,如飞机机翼影响时。它涉及到流体动力学领域和其子领域气体动力学所涵盖的主题。空气动力学一词通常与气体动力学同义使用,区别在于 “气体动力学 “适用于研究所有气体的运动,而不限于空气。空气动力学的正式研究在现代意义上开始于18世纪,尽管对空气动力阻力等基本概念的观察记录要早得多。大多数早期的空气动力学努力都是为了实现比空气重的飞行,这是由奥托-利连塔尔在1891年首次证明的。从那时起,通过数学分析、经验近似、风洞实验和计算机模拟对空气动力学的使用,为比空气重的飞行和其他一些技术的发展奠定了合理基础。最近的空气动力学工作集中在与可压缩流、湍流和边界层有关的问题上,并且越来越具有计算的性质。
空气动力学Aerodynamics代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。最高质量的空气动力学Aerodynamics作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此空气动力学Aerodynamics作业代写的价格不固定。通常在专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
同学们在留学期间,都对各式各样的作业考试很是头疼,如果你无从下手,不如考虑my-assignmentexpert™!
my-assignmentexpert™提供最专业的一站式服务:Essay代写,Dissertation代写,Assignment代写,Paper代写,Proposal代写,Proposal代写,Literature Review代写,Online Course,Exam代考等等。my-assignmentexpert™专注为留学生提供Essay代写服务,拥有各个专业的博硕教师团队帮您代写,免费修改及辅导,保证成果完成的效率和质量。同时有多家检测平台帐号,包括Turnitin高级账户,检测论文不会留痕,写好后检测修改,放心可靠,经得起任何考验!
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
我们在物理Physical代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的物理Physical代写服务。我们的专家在空气动力学Aerodynamics代写方面经验极为丰富,各种空气动力学Aerodynamics相关的作业也就用不着说。
物理代写|空气动力学代写Aerodynamics代考|Classical Aerodynamics
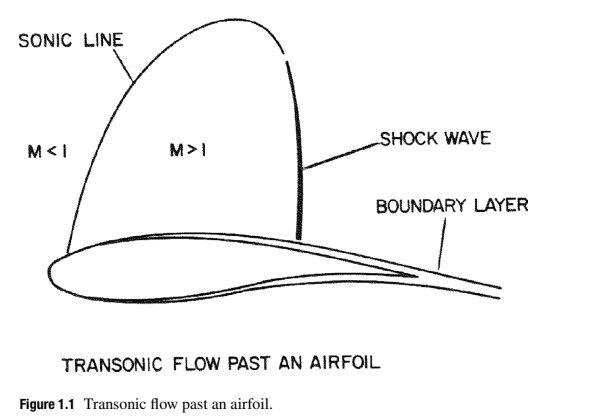
This chapter surveys some of the principal developments of computational aerodynamics, with a focus on aeronautical applications. It is written with the perspective that computational mathematics is a natural extension of classical methods of applied mathematics, which has enabled the treatment of more complex, in particular nonlinear, mathematical models, and also the calculation of solutions in very complex geometric domains not amenable to classical techniques such as the separation of variables.
This is particularly true for aerodynamics. Efficient flight can be achieved only by establishing highly coherent flows. Consequently there are many important applications where it is not necessary to solve the full Navier-Stokes equations in order to gain an insight into the nature of the flow, and useful predictions can be made with simplified mathematical models. It was already recognized by Prandtl in 1904 (Prandtl 1904, Schlichting \& Gersten 1999), essentially contemporaneous with the first successful flights of the Wright brothers, that in flows at the large Reynolds numbers typical of powered flight, viscous effects are important chiefly in thin shear layers adjacent to the surface. While these boundary layers play a critical role in determining whether the flow will separate and how much circulation will be generated around a lifting surface, the equations of inviscid flow are a good approximation in the bulk of the flow field external to the boundary layer. In the absence of separation, a first estimate of the effect of the boundary layer is provided by regarding it as increasing the effective thickness of the body. This procedure can be justified by asymptotic analysis (Van Dyke 1964, Ashley \& Landahl 1985).
The classical treatment of the external inviscid flow is based on Kelvin’s theorem that in the absence of discontinuities, the circulation around a material loop remains constant. Consequently an initially irrotational flow remains irrotational. This allows us to simplify the equations further by representing the velocity as the gradient of a potential. If the flow is also regarded as incompressible, the governing equation reduces to Laplace’s equation. These simplifications provided the basis for the classical airfoil theory of Joukowsky (Glauert 1926) and Prandtl’s wing theory (Prandtl \& Tietjens 1957, Ashley \& Landahl 1985). Supersonic flow over slender bodies at Mach numbers greater than two is also well represented by the linearized equations. Techniques for the solution of linearized flow were perfected in the period 1935-1950, particularly by W.D. Hayes, who derived the supersonic area rule (Hayes 1947).
物理代写|空气动力学代写Aerodynamics代考|The Emergence of Computational Aerodynamics and its Application
to Transonic Flow
Prior to 1960 , computational methods were hardly used in aerodynamic analysis, although they were already widely used for structural analysis. The NACA 6 series of airfoils had been developed during the forties, using hand computation to implement the Theodorsen method for conformal mapping (Theodorsen 1931). The first major success in computational aerodynamics was the introduction of boundary integral methods by Hess and Smith (1962) to calculate potential flow over an arbitrary configuration. Generally known in the aeronautical community as panel methods, these continue to be used to the present day to make initial predictions of low speed aerodynamic characteristics of preliminary designs. It was the compelling need, however, both to predict transonic flow and to gain a better understanding of its properties and character, that was a driving force for the development of computational aerodynamics through the period 1970-1990.
In the case of military aircraft capable of supersonic flight, the high drag associated with high $g$ maneuvers forces them to be performed in the transonic regime. In the case of commercial aircraft, the importance of transonic flow stems from the Breguet range equation. This provides a good first estimate of range as
$$
R=\frac{V}{s f_{c}} \frac{L}{D} \log \frac{W_{0}+W_{f}}{W_{0}}
$$
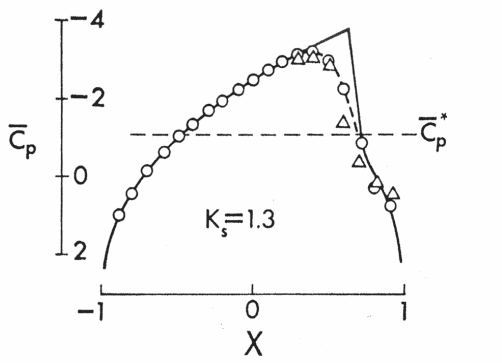
空气动力学代写
物理代写|空气动力学代写AERODYNAMICS代考|CLASSICAL AERODYNAMICS
本章概述了计算空气动力学的一些主要发展,重点是航空应用。它的写作观点认为,计算数学是应用数学经典方法的自然延伸,它可以处理更复杂的,特别是非线 性的数学模型,也可以计算非常复杂的几何域中的解经典技术,例如变量分离。
对于空气动力学来说尤其如此。只有建立高度连苺的流动,才能实现高效飞行。因此,在许多重要的应用中,无需求解完整的 Navier-Stokes 方程即可深入了解流动 的性质,并且可以使用简化的数学模型进行有用的预测。普朗特早在 1904 年就已经认可了它Prandtl1904, Schlichting\&Gersten1999,基本上与莱特兄弟的第 一次成功飞行同时,在动力飞行典型的大雷诺数的流动中,粘性效应主要在靠近表面的薄型切层中很重要。虽然这些边界层在确定流动是否分离以及在升力面周围 产生多少环流方面发挥着关键作用,但无粘性流动方程是边界层外部大部分流场的良好近似。在没有分离的情况下,通过将边界层视为增加主体的有效厚度来提供 对边界层影响的初步估计。这个过程可以通过渐近分析来证明VanDyke1964, Ashley\&Landahl1985.
外部无粘性流动的经典处理基于开尔文定理,即在没有不连续性的情况下,围绕物质环的唕环保持恒定。因此,最初无旋的流动保持无旋。这允许我们通过将速度 表示为电位梯度来进一步简化方程。如果流动也被认为是不可压缩的,则控制方程简化为拉普拉斯方程。这些简化为 Joukowsky 的经典翼型理论提供了基础 Glauert 1926和普朗特的机翼理论Prandtl\&Tietjens 1957, Ashley\&Landahl1985. 线性化方程也很好地表示了马赫数大于 2 的细长物体上的超音速流动。求 解线性化流的技术在 1935-1950 年间得到了完善,特别是 WD Hayes,他推导出了超音速面积规则 Hayes 1947 .
物理代写|空气动力学代写AERODYNAMICS代考|THE EMERGENCE OF COMPUTATIONAL AERODYNAMICS AND ITS APPLICATION TO TRANSONIC FLOW
在 1960 年之前,计算方法几乎没有用于空气动力学分析,尽管它们已经广泛用于结构分析。NACA 6 系列机鳎是在 40 年代开发的,使用手动计算来实现共形映射的 Theodorsen 方法Theodorsen1931. 计算空气动力学的第一个重大成功是 Hess 和 Smith 引入边界积分方法1962计算任意配置上的潜在流量。在航空界通常称为面 板方法,这些方法至今仍被用于对初步设计的低速空气动力学特性进行初步预测。然而,预测跨音速流和更好地了解其特性和特征是迫切需要,这是 1970-1990 年 间计算空气动力学发展的驱动力。
在能够进行超音速飞行的军用飞机的情况下,与高阻力相关的高阻力 $g$ 演习迫使它们在跨音速状态下进行。就商用飞机而言,跨音速流的重要性源于宝玑射程方 程。这提供了一个很好的范围的初步估计,因为
$$
R=\frac{V}{s f_{c}} \frac{L}{D} \log \frac{W_{0}+W_{f}}{W_{0}}
$$

物理代写|空气动力学代写Aerodynamics代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
微观经济学代写
微观经济学是主流经济学的一个分支,研究个人和企业在做出有关稀缺资源分配的决策时的行为以及这些个人和企业之间的相互作用。my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学Mathematics代写服务。我们的专家在图论代写Graph Theory代写方面经验极为丰富,各种图论代写Graph Theory相关的作业也就用不着 说。
线性代数代写
线性代数是数学的一个分支,涉及线性方程,如:线性图,如:以及它们在向量空间和通过矩阵的表示。线性代数是几乎所有数学领域的核心。
博弈论代写
现代博弈论始于约翰-冯-诺伊曼(John von Neumann)提出的两人零和博弈中的混合策略均衡的观点及其证明。冯-诺依曼的原始证明使用了关于连续映射到紧凑凸集的布劳威尔定点定理,这成为博弈论和数学经济学的标准方法。在他的论文之后,1944年,他与奥斯卡-莫根斯特恩(Oskar Morgenstern)共同撰写了《游戏和经济行为理论》一书,该书考虑了几个参与者的合作游戏。这本书的第二版提供了预期效用的公理理论,使数理统计学家和经济学家能够处理不确定性下的决策。
微积分代写
微积分,最初被称为无穷小微积分或 “无穷小的微积分”,是对连续变化的数学研究,就像几何学是对形状的研究,而代数是对算术运算的概括研究一样。
它有两个主要分支,微分和积分;微分涉及瞬时变化率和曲线的斜率,而积分涉及数量的累积,以及曲线下或曲线之间的面积。这两个分支通过微积分的基本定理相互联系,它们利用了无限序列和无限级数收敛到一个明确定义的极限的基本概念 。
计量经济学代写
什么是计量经济学?
计量经济学是统计学和数学模型的定量应用,使用数据来发展理论或测试经济学中的现有假设,并根据历史数据预测未来趋势。它对现实世界的数据进行统计试验,然后将结果与被测试的理论进行比较和对比。
根据你是对测试现有理论感兴趣,还是对利用现有数据在这些观察的基础上提出新的假设感兴趣,计量经济学可以细分为两大类:理论和应用。那些经常从事这种实践的人通常被称为计量经济学家。
Matlab代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。

