如果你也在 怎样代写计算物理Computational physics PHY4905/5905这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。计算物理Computational physics是研究和实施数值分析,以解决物理学中已经存在定量理论的问题。从历史上看,计算物理学是现代计算机在科学中的第一个应用,现在是计算科学的一个子集。它有时被视为理论物理学的一个分支(或分支),但也有人认为它是理论物理学和实验物理学之间的一个中间分支–一个补充理论和实验的研究领域。
计算物理Computational physics在物理学中,基于数学模型的不同理论对系统的行为方式提供了非常精确的预测。不幸的是,为了产生一个有用的预测,解决一个特定系统的数学模型往往是不可行的。例如,当解决方案没有闭合形式的表达,或过于复杂时,就会出现这种情况。在这种情况下,需要进行数字近似。计算物理学是处理这些数值近似的学科:解决方案的近似被写成有限的(通常是大量的)简单数学运算(算法),计算机被用来执行这些运算,并计算出近似的解决方案和各自的误差。
计算物理Computational physics代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。最高质量的计算物理Computational physics作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此计算物理Computational physics作业代写的价格不固定。通常在专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
同学们在留学期间,都对各式各样的作业考试很是头疼,如果你无从下手,不如考虑my-assignmentexpert™!
my-assignmentexpert™提供最专业的一站式服务:Essay代写,Dissertation代写,Assignment代写,Paper代写,Proposal代写,Proposal代写,Literature Review代写,Online Course,Exam代考等等。my-assignmentexpert™专注为留学生提供Essay代写服务,拥有各个专业的博硕教师团队帮您代写,免费修改及辅导,保证成果完成的效率和质量。同时有多家检测平台帐号,包括Turnitin高级账户,检测论文不会留痕,写好后检测修改,放心可靠,经得起任何考验!
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
我们在物理Physical代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的物理Physical代写服务。我们的专家在计算物理Computational physics代写方面经验极为丰富,各种计算物理Computational physics相关的作业也就用不着说。
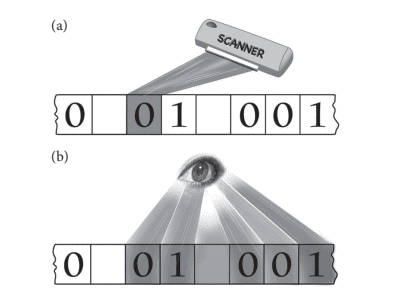
物理代写|计算物理代写Computational physics代考|Turing’s Analysis
The Church-Turing thesis asserts that every effectively computable function is a general recursive function (or Turing machine computable). But what are the grounds for this thesis? In his book, Kleene (1952) lists four kinds of justification. The first two are the arguments of confluence and of non-refutation, which are prevalent in current textbooks in computability, logic, and automata theory. The confluence argument states that many characterizations of computation that differ in their goals, approaches, and details nonetheless encompass the same class of computable functions. As we have seen, the confluence of four such characterizations appeared in 1936, and many more characterizations have followed. ${ }^{20}$ The non-refutation argument states that the thesis, though refutable, has not been refuted despite the many efforts and attempts to find a counterexample. ${ }^{21}$ Both arguments are of an inductive nature: the more examples you have (either of yet another precise characterization of computability, or of yet another computable function that turns out to be recursive), the more the thesis is confirmed. Indeed, these arguments strengthen the impression that the thesis is not subject to mathematical proof.
The other two arguments are more direct, in that they deal, in one way or another, with the process of computing. ${ }^{22}$ One argument, put forward by Church (1936a: 100-102), is known as the step-by-step argument. ${ }^{23}$ Using Gödel’s notion of representability (Gödel 1931; Kleene 1936), Church characterizes an effectively computable function as one that is calculable in logic. As he puts it:
Let us call a function $F$ of one positive integer calculable within the logic if there exists an expression $f$ in the logic such that ${f}(\mu)=v$ is a theorem when and only when $F(m)=n$ is true, $\mu$ and $v$ being the expressions which stand for the positive integers $m$ and $n$. (1936a: 101)
The rationale behind this characterization is the tight relationship between effective computation and logical derivation. A function is (intentionally) effectively computable only if there is a derivation of the corresponding (“representing”) logical formula (“expression”), when we replace the number values $m$ and $n$ with the corresponding constants $m$ and $n$. This characterization highlights the close kinship that existed between formal systems and effective computability at the time. On the one hand, a formal system is characterized in terms of effective computability; on the other, effective computability is defined in terms of formal derivability. A variant of this characterization appears in Turing (1936), Hilbert and Bernays (1939), Church (1941: 41), and Gödel (1946). ${ }^{24}$ Given this characterization, Church proceeds to show that if each step of the derivation is general recursive, then the defined function is recursive as well. What is left open, however, is the assumption that these basic steps must be recursive. ${ }^{25}$ As Sieg points out, this argument is “semicircular in the sense that he [Church] assumed without good reason that the necessarily elementary calculation steps have to be recursive” (2006: 193).
物理代写|计算物理代写Computational physics代考|Who Is “the Computer”?
The claim that Turing’s analysis essentially applies to human computers was underscored by his student Robin Gandy. ${ }^{33}$ In his 1980 paper on computability, Gandy wrote:
Both Church and Turing had in mind calculation by an abstract human being using some mechanical aids (such as paper and pencil). The word “abstract” indicates that the argument makes no appeal to the existence of practical limits on time and space. (1980: 123-124)
In his historical 1988 paper, Gandy once again emphasized that Turing’s “computability” relates to calculations by an ideal human, and that Turing “makes no reference whatsoever to calculating machines” (Gandy 1988: 83). In Gandy’s posthumously published introduction to the 1936 paper, he wrote that Turing “considers the actions of an abstract human being who is making a calculation” (2001: 11).
There are several reasons to support this human-oriented line of interpretation. One is the fact that the computers at the time of Turing’s statements were humans, not machines: “It is not surprising that Turing does not mention machines. Numerical calculation in 1936 was carried out by human beings” (Gandy 2001: 12). ${ }^{34}$ The first programmable, general-purpose computers were only manufactured in the 1940 s. A second reason is the highly anthropomorphic language that Turing uses to describe “the computer.” “Turing’s analysis is quite explicitly concerned with calculations performed by a human being; there is no reference to machines other than those which he introduces to imitate the actions of a human computor” (Gandy 2001: 12). Third, the analysis essentially exploits the limitations of human computers, not of machines in general: “Turing’s analysis of computation by a human being does not apply directly to mechanical devices” (Gandy 1980: 123), and “There are crucial steps in Turing’s analysis where he appeals to the fact that the calculation is being carried out by a human being” (p. 124).
A decisive point in favor of the human-oriented interpretation, in my view, is that it places Turing’s pioneering work on effective computability in its appropriate historical and philosophical context-namely, the role of effective computation in logic and mathematics (as discussed in Section 2.1). In this regard, the notion of effective procedure is tightly connected to $u s-$ the human computers. The notions of decidability, formal derivability, and formal systems are closely linked to what a human can or cannot do, at least in principle, when using an effective procedure. This does not mean that a machine cannot compute effectively, but rather that the benchmark of what counts as effectively computable is the human computer: something is effectively computable only if it can be computed by an idealized human being. To ignore the human connection is to miss a key and distinct aspect of the notion of effective computation in the context of logic and mathematics.
计算物理代写
物理代写|计算物理代写COMPUTATIONAL PHYSICS代 考|TURING’S ANALYSIS
Church-Turing 论文断言,每个有效可计算函数都是一般递归函数orTuringmachinecomputable. 但这篇论文的依据是什么? 在他的书中,克莱恩1952列出了四 种理由。前两个是合流和不可反驳的论点,它们在当前的可计算性、逻辑和自动机理论教科书中很普遍。融合论点指出,许多在目标、方法和细节上不同的计算特 征都包含同一类可计算函数。正如我们所看到的,1936年出现了四种这样的特征的汇合,并且随后出现了更茤的特征。 20 不可反驳论点指出,该论点虽然可以反衣 栚,但尽管付出了许多努力和営试寻找反例,但仍末被反驳。 ${ }^{21}$ 这两个论点都具有归纳性质:您拥有的示例越多
eitherofyetanotherprecisecharacterizationofcomputability, orofyetanothercomputable functionthatturnsouttoberecursive,越多的论文被证实。 事实上,这些论点强化了论文不受数学证明的印象。
其他两个论点更直接,因为它们以一种或另一种方式处理计算过程。 ${ }^{22}$ 丘奇提出的一个论点 $1936 a: 100-102$, 被称为逐步论证。 ${ }^{23}$ 使用哥德尔的可表示性概念 Gödel1931; Kleene1936, Church 将有效可计算函数描述为逻辑上可计算的函数。正如他所说:
让我们调用一个函数 $F$ 如果存在表达式,则可以在逻辑内计算一个正整数 $f$ 在这样的楞辑 $f(\mu)=v$ 当且仅当是一个定理 $F(m)=n$ 是真的, $\mu$ 和 $v$ 是代表正整数的表 达式 $m$ 和 $n .1936 a: 101$
这种表征背后的基本原理是有效计算和楞辑推导之间的累密关系。一个函数是intentionally仅当存在对应的推导时才可有效计算 “representing”楞辑公式 “expression”, 当我们䒨换数值时 $m$ 和 $n$ 与相应的常数 $m$ 和 $n$. 这种特征突出了当时形式系统和有效可计算性之间存在的密切关系。一方面,形式系统的特点是有效 的可计算性;另一方面,有效可计算性是根据形式可推导性定义的。这种表征的一个变体出现在图灵 1936 , 希尔伯特和伯奈斯1939,教会 $1941: 41$, 和哥德尔 1946. ${ }^{24}$ 鉴于这种特征,Church 继续表明,如果推导的每一步都是一般递归的,那么定义的函数也是递归的。然而,开放的是假设这些基本步骤必须是递归的。 ${ }^{25}$ 正如 Sieg 所指出的,这个论点是”半圆形的,因为他
Church
没有充分理由假设必要的基本计算步骤必须是递归的”2006: 193 .
物理代写|计算物理代写COMPUTATIONAL PHYSICS代考|WHO IS “THE COMPUTER”?
他的学生罗宾日迪强调了图灵的分析基本上适用于人类计算机的说法。 ${ }^{33}$ 在他 1980 年关于可计算性的论文中,Gandy写道:
Church和 Turing 都想到了由一个抽象的人使用一些机械辅助进行的计算suchaspaperandpencil. “抽象”一词表明该论点对时间和空间的实际限制的存在没有吸引低 力。 $1980: 123-124$
在他 1988 年的历史论文中,甘迪再次强调,图灵的“可计算性”与理想人类的计算有关,而图灵“完全没有提到计算机”Gandy1988: 83 . 在甘迪死后发表的对 1936 年论文的介绍中,他写道,图灵“考虑了一个正在计算的抽象人的行为” $2001: 11$.
支持这种以人为本的解释路线有几个原因。一是在图灵发表声明时计算机是人类,而不是机器这一事实:“图灵没有提到机器并不奇怪。1936年的数值计算是由人 类进行的”Gandy2001:12. ${ }^{34}$ 第一台可编程的通用计算机是在 1940 年代才制造出来的。第二个原因是图灵用来描述“计算机”的高度拟人化的语言。“图灵的分析非 常明确地关注人类执行的计算;除了他介绍的用于模仿人类计算机动作的机器外,没有提到其他机楍” $G a n d y 2001: 12$. 第三,该分析本质上是利用了人类计算机 的局限性,而不是一般机器的局限性:“图灵对人类计算的分析并不直接适用于机械设备”Gandy $1980: 123$ ,以及“图灵的分析中有几个关键步骤,他呼吁计算是 由人粂执行的这一事实”p. 124 .
在我看来,支持以人为本的解释的一个决定性点是,它将图灵关于有效可计算性的开创性工作置于其适当的历史和哲学背景中,即有效计算在逻辑和数学中的作用 asdiscussedinSection2.1. 在这方面,有效程序的概念与 $u s$-人类计算机。可判定性、形式派生性和形式系统的概念与人类在使用有效程序时可以做什么或不可 以做什么密切相关,至少在原则上是这样。这并不意味着一台机器不能有效地计算,而是认为有效可计算的基准是人类计算机:只有当它可以由理想化的人类计算 时,它才是有效可计算的。忽略人类联系就是错过逻辑和数学背景下有效计算概念的一个关键和独特的方面。

物理代写|计算物理代写Computational physics代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
微观经济学代写
微观经济学是主流经济学的一个分支,研究个人和企业在做出有关稀缺资源分配的决策时的行为以及这些个人和企业之间的相互作用。my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学Mathematics代写服务。我们的专家在图论代写Graph Theory代写方面经验极为丰富,各种图论代写Graph Theory相关的作业也就用不着 说。
线性代数代写
线性代数是数学的一个分支,涉及线性方程,如:线性图,如:以及它们在向量空间和通过矩阵的表示。线性代数是几乎所有数学领域的核心。
博弈论代写
现代博弈论始于约翰-冯-诺伊曼(John von Neumann)提出的两人零和博弈中的混合策略均衡的观点及其证明。冯-诺依曼的原始证明使用了关于连续映射到紧凑凸集的布劳威尔定点定理,这成为博弈论和数学经济学的标准方法。在他的论文之后,1944年,他与奥斯卡-莫根斯特恩(Oskar Morgenstern)共同撰写了《游戏和经济行为理论》一书,该书考虑了几个参与者的合作游戏。这本书的第二版提供了预期效用的公理理论,使数理统计学家和经济学家能够处理不确定性下的决策。
微积分代写
微积分,最初被称为无穷小微积分或 “无穷小的微积分”,是对连续变化的数学研究,就像几何学是对形状的研究,而代数是对算术运算的概括研究一样。
它有两个主要分支,微分和积分;微分涉及瞬时变化率和曲线的斜率,而积分涉及数量的累积,以及曲线下或曲线之间的面积。这两个分支通过微积分的基本定理相互联系,它们利用了无限序列和无限级数收敛到一个明确定义的极限的基本概念 。
计量经济学代写
什么是计量经济学?
计量经济学是统计学和数学模型的定量应用,使用数据来发展理论或测试经济学中的现有假设,并根据历史数据预测未来趋势。它对现实世界的数据进行统计试验,然后将结果与被测试的理论进行比较和对比。
根据你是对测试现有理论感兴趣,还是对利用现有数据在这些观察的基础上提出新的假设感兴趣,计量经济学可以细分为两大类:理论和应用。那些经常从事这种实践的人通常被称为计量经济学家。
Matlab代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。

