如果你也在 怎样代写费曼图Feynman Diagram MATHS5054这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。费曼图Feynman Diagram是对量子力学或统计场理论的过渡振幅或相关函数的微扰贡献的图形表示。在量子场论的经典表述中,费曼图表示微扰S矩阵的威克展开中的一个项。另外,量子场论的路径积分表述将过渡振幅表示为系统从初始状态到最终状态的所有可能历史的加权和,以粒子或场为单位。然后,过渡振幅被赋予量子系统的初始状态和最终状态之间的S矩阵元素。
费曼图Feynman Diagram在理论物理学中,是描述亚原子粒子行为和相互作用的数学表达式的图解。该方案以美国物理学家理查德-费曼的名字命名,他在1948年引入了该图。亚原子粒子的相互作用可能是复杂和难以理解的;费曼图为本来是神秘和抽象的公式提供了一个简单的可视化。据大卫-凯泽说:”自20世纪中期以来,理论物理学家越来越多地转向这一工具,以帮助他们进行关键的计算。费曼图几乎彻底改变了理论物理学的每一个方面。”虽然该图主要应用于量子场理论,但也可用于其他领域,如固态理论。弗兰克-威尔切克写道,为他赢得2004年诺贝尔物理学奖的计算 “如果没有费曼图,简直无法想象,正如[威尔切克]的计算建立了一条生产和观测希格斯粒子的路线一样” 。
费曼图Feynman Diagram代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。最高质量的费曼图Feynman Diagram作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此费曼图Feynman Diagram作业代写的价格不固定。通常在专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
同学们在留学期间,都对各式各样的作业考试很是头疼,如果你无从下手,不如考虑my-assignmentexpert™!
my-assignmentexpert™提供最专业的一站式服务:Essay代写,Dissertation代写,Assignment代写,Paper代写,Proposal代写,Proposal代写,Literature Review代写,Online Course,Exam代考等等。my-assignmentexpert™专注为留学生提供Essay代写服务,拥有各个专业的博硕教师团队帮您代写,免费修改及辅导,保证成果完成的效率和质量。同时有多家检测平台帐号,包括Turnitin高级账户,检测论文不会留痕,写好后检测修改,放心可靠,经得起任何考验!
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
我们在物理Physical代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的物理Physical代写服务。我们的专家在费曼图Feynman Diagram代写方面经验极为丰富,各种费曼图Feynman Diagram相关的作业也就用不着说。
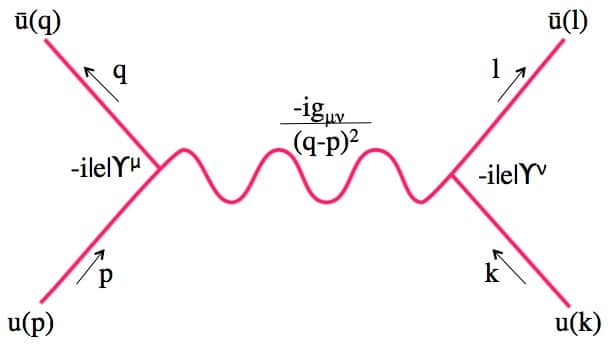
物理代写|费曼图代写Feynman Diagram代考|A Tool for Organizing Calculations
“Like the silicon chip of more recent years, the Feynman diagram was bringing computation to the masses.” Thus Julian Schwinger, ‘ displaying a hint of both disdain and admiration, appraises the enormous impact of Feynman diagrams as a mathematical tool on the daily work of theoretical physicists. And indeed, since Richard $\mathrm{P}$. Feynman (1918-1988) invented them, around the year 1948, and Freeman J. Dyson subsequently systematized them, these diagrams have undeniably become an indispensable tool for performing calculations in modern quantum field theory. They are omnipresent in the theoretical treatments of an important class of elementary particle phenomena, in particular quantum electrodynamics (QED). In modern textbooks on quantum field theory-I will quote from one of them below-they take centre stage, while the teaching of their use is one of the essential components in courses on the subject.
Feynman diagrams enable one to find the relevant expressions in an approximate solution (perturbative expansion) to the equations that describe the dynamics of a quantum electrodynamic system. From the conception of the process as a sequence of particle creations and annihilations, one can produce a schematic drawing that relates these creation and annihilation events. The diagram thus obtained can then be translated, element by element, into a complex mathematical expression, the evaluation of which yields an observable quantity that characterizes the physical system (amplitudes of transition probabilities).
At the beginning of their widely used textbook on quantum field theory, Michael Peskin and Daniel Schroeder introduce Feynman diagrams in the following way:
a diagram, and then use the diagram to write the mathematical form of the quantummechanical amplitude for that process to occur. (Peskin and Schroeder 1995, p. 3)
We know of no methods that can exactly solve the equations that supposedly describe a quantum electrodynamic system, and no candidate for such an exact method even exists. Therefore, one has to turn to approximate solutions, such as the so-called perturbative expansion. For this method of solution Feynman provided an appropriate tool:
The bad news is that even for this simplest of QED processes $\left[e^{+} e^{-} \rightarrow \mu^{+} \mu^{-}\right]$, the exact expression for $\mathcal{M}$ [the quantum-mechanical amplitude for the process to occur] is not known. $[\ldots]$ The best we can do is obtain a formal expression for $\mathcal{M}$ as a perturbation series in the strength of the electromagnetic interaction, and evaluate the first few terms in this series.
The good news is that Feynman has invented a beautiful way to organize and visualize the perturbation series: the method of Feynman diagrams. Roughly speaking, the diagrams display the flow of electrons and photons during the scattering process. (Peskin and Schroeder 1995, p. 5)
物理代写|费曼图代写Feynman Diagram代考|Tempting but Incorrect Interpretations
While Peskin and Schroeder (1995) aptly characterize Feynman diagrams as a tool for organizing perturbative calculations, Rom Harré (1988, pp. 62, 64) writes of a way of “parsing the amplitudes”. To perform the “parsing” process, one has first to “imagine a process that can be carried out by electrons and photons”, as Peskin and Schroeder state, and then draw diagrams that “display the flow of electrons and photons during the scattering process”.
However, some textbooks explicitly warn the reader not to take too literally the interpretation that these diagrams represent scattering processes. The diagrams represent the scattering process only in an extremely abstract way. For most authors the safest way of using Feynman diagrams is, therefore, to consider them as nothing more than an abbreviation of the mathematical expressions that one has to deal with in the calculations:
Please understand: these Feynman diagrams are purely symbolic; they do not represent particle trajectories (as you might see them in, say, a bubble chamber photograph). The vertical dimension is time, and horizontal spacings do not correspond to physical separations. For instance, in Bhabha scattering [see Fig. 1.1] the electron and positron are attracted, not repelled as the diverging lines might seem to suggest). All the diagram says is: “Once there was an electron and a positron; they exchanged a photon; then there was an electron and a positron again.” Each Feynman diagram actually stands for a particular number, which can be calculated using the so-called Feynman rules. (Griffiths 1987, p. 59, emph. in the original)
费曼图代写
物理代写|费曼图代写FEYNMAN DIAGRAM代考|A TOOL FOR ORGANIZING CALCULATIONS
“就像最近几年的砫芯片一样,费曼图正在将计算带给大众。”因此,朱利安·施温格 (Julian Schwinger) 表现出既不屑又钦佩的暗示,他评价了费㬅图作为数学工具 对理论物理学家日常工作的巨大影响。事实上,自从理查德 $\mathrm{P} \ldots \ldots$ 费䍒 $1918-1988$ 在 1948 年左右发明了它们,弗里曼·戴森随后将它们系统化,这些图无疑已成 为现代量子场论中进行计算的不可或缺的工具。它们在一类重要的基本粒子现象的理论处理中无处不在,特别是量子电动力学 $Q E D$. 在有关量子场论的现代教科书 中一一我将在下面引用其中一本一一它们占据了中心位置,而使用它们的教学是该主题课程的重要组成部分之一。
费曼图使人们能够在近似解中找到相关表达式perturbativeexpansion到描述量子电动力学系统动力学的方程。从这个过程作为一系列粒子创造和湮夾的概念, 人们可以产生一个与这些创造和湮大事件相关的示意图。然后可以将由此获得的图表逐个元素转换为复杂的数学表达式,对其进行评估会产生表征物理系统的可观 䕓量 amplitudesoftransitionprobabilities.
在他们广泛使用的量子场论教科书的开头, Michael Peskin 和 Daniel Schroeder 通过以下方式介绍了费曼图:
一个图表,然后使用该图表写出该过程发生的量子力学幅度的数学形式。PeskinandSchroeder $1995, p .3$
我们知道没有任何方法可以精确地求解据称描述量子电动力学系统的方程,甚至不存在这种精确方法的候选者。因此,不得不求助于近似解,例如所佣的微扰展 开。对于䢒种解决方法,费夢提供了一个合适的工具:
坏消息是,即使对于这个最简单的 QED 过程 $\left[e^{+} e^{-} \rightarrow \mu^{+} \mu^{-}\right]$, 的精确表达式 $\mathcal{M}$
thequantum – mechanicalamplitude fortheprocesstooccur
不知道。[...我们能做的最好的事情是获得一个正式的表达式 $\mathcal{M}$ 作为电磁相互作用强度的扰动系列,并评估该系列中的前几项。
好消息是,艴曼发明了一种组织和可视化扰动级数的漂亮方法:费曼图的方法。粗略地说,这些图表显示了散射过程中电子和光子的流动。
PeskinandSchroeder $1995, p .5$
物理代写|费曼图代写FEYNMAN DIAGRAM代考|TEMPTING BUT INCORRECT INTERPRETATIONS
而佩斯金和施罗德1995恰当地将费曼图描述为组织微扰计算的工具,Rom Harré1988, pp. 62, 64写了一种“解析幅度”的方法。要执行“解析”过程,首先必须“想象一 个可以由电子和光子执行的过程”,如 Peskin 和 Schroeder 状态,然后绘制“显示电子和光子在散射过程中的流动”的图表”。
然而,一些教科书明确警告读者不要过于字面地理解这些图代表散射过程。这些图表仅以极其抽象的方式表示散射过程。因此,对于大多数作者来说,使用艴曼图 最安全的方法就是将它们视为在计算中必须处理的数学表达式的㜚写:
请理解:这些费曼图纯粹是象征性的;它们不代表粒子轨迹asyoumightseethemin, say, abubblechamberphotograph. 垂直维度是时间,水平间距不对应物理 间隔。例如,在 Bhabha散射中
seefig. $1.1$
电子和正电子被吸引,而不是像发散线似乎暗示的那样被排斥)。这张图说的是:“曾经有一个电子和一个正电子;他们交换了一个光子;然后又出现了一个电子 和一个正电子。”每个费曼图实际上代表一个特定的数字,可以使用所谓的费畠规则来计算。Griffiths $1987, p .59$, emph. intheoriginal

物理代写|费曼图代写Feynman Diagram代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
微观经济学代写
微观经济学是主流经济学的一个分支,研究个人和企业在做出有关稀缺资源分配的决策时的行为以及这些个人和企业之间的相互作用。my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学Mathematics代写服务。我们的专家在图论代写Graph Theory代写方面经验极为丰富,各种图论代写Graph Theory相关的作业也就用不着 说。
线性代数代写
线性代数是数学的一个分支,涉及线性方程,如:线性图,如:以及它们在向量空间和通过矩阵的表示。线性代数是几乎所有数学领域的核心。
博弈论代写
现代博弈论始于约翰-冯-诺伊曼(John von Neumann)提出的两人零和博弈中的混合策略均衡的观点及其证明。冯-诺依曼的原始证明使用了关于连续映射到紧凑凸集的布劳威尔定点定理,这成为博弈论和数学经济学的标准方法。在他的论文之后,1944年,他与奥斯卡-莫根斯特恩(Oskar Morgenstern)共同撰写了《游戏和经济行为理论》一书,该书考虑了几个参与者的合作游戏。这本书的第二版提供了预期效用的公理理论,使数理统计学家和经济学家能够处理不确定性下的决策。
微积分代写
微积分,最初被称为无穷小微积分或 “无穷小的微积分”,是对连续变化的数学研究,就像几何学是对形状的研究,而代数是对算术运算的概括研究一样。
它有两个主要分支,微分和积分;微分涉及瞬时变化率和曲线的斜率,而积分涉及数量的累积,以及曲线下或曲线之间的面积。这两个分支通过微积分的基本定理相互联系,它们利用了无限序列和无限级数收敛到一个明确定义的极限的基本概念 。
计量经济学代写
什么是计量经济学?
计量经济学是统计学和数学模型的定量应用,使用数据来发展理论或测试经济学中的现有假设,并根据历史数据预测未来趋势。它对现实世界的数据进行统计试验,然后将结果与被测试的理论进行比较和对比。
根据你是对测试现有理论感兴趣,还是对利用现有数据在这些观察的基础上提出新的假设感兴趣,计量经济学可以细分为两大类:理论和应用。那些经常从事这种实践的人通常被称为计量经济学家。
Matlab代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。