如果你也在 怎样代写数字信号处理Digital Signal Processing ECE513这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。数字信号处理Digital Signal Processing是指使用数字处理,如通过计算机或更专业的数字信号处理器,来执行各种信号处理操作。以这种方式处理的数字信号是一连串的数字,代表时间、空间或频率等领域中连续变量的样本。在数字电子学中,数字信号被表示为脉冲序列,它通常由晶体管的开关产生。
数字信号处理Digital Signal Processing模拟信号处理是信号处理的子领域。DSP的应用包括音频和语音处理、声纳、雷达和其他传感器阵列处理、频谱密度估计、统计信号处理、数字图像处理、数据压缩、视频编码、音频编码、图像压缩、电信的信号处理、控制系统、生物医学工程和地震学等。数字信号处理器(DSP)将现实世界的信号,如语音、音频、视频、温度、压力或位置,经过数字化处理,然后以数学方式处理它们。数字信号处理器被设计用于快速执行数学功能,如 “加”、”减”、”乘 “和 “除”。
数字信号处理Digital Signal Processing代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。最高质量的数字信号处理Digital Signal Processing作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此数字信号处理Digital Signal Processing作业代写的价格不固定。通常在专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
同学们在留学期间,都对各式各样的作业考试很是头疼,如果你无从下手,不如考虑my-assignmentexpert™!
my-assignmentexpert™提供最专业的一站式服务:Essay代写,Dissertation代写,Assignment代写,Paper代写,Proposal代写,Proposal代写,Literature Review代写,Online Course,Exam代考等等。my-assignmentexpert™专注为留学生提供Essay代写服务,拥有各个专业的博硕教师团队帮您代写,免费修改及辅导,保证成果完成的效率和质量。同时有多家检测平台帐号,包括Turnitin高级账户,检测论文不会留痕,写好后检测修改,放心可靠,经得起任何考验!
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
我们在电子代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的电子代写服务。我们的专家在电路基础Circuit Fundamentals代写方面经验极为丰富,各种电路基础Circuit Fundamentals相关的作业也就用不着说。
电子代写|数字信号处理代写Digital Signal Processing代考|Matrix Decomposition
Any matrix, whether real or complex valued square or rectangular, may be decomposed into a certain number of simpler matrices that provide us with a better understanding of the associated transformation.
The Eigenvalue Decomposition
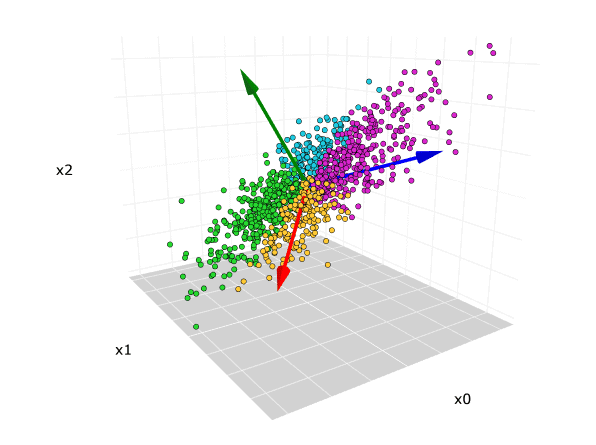
The first decomposition that we will examine is the eigenvalue decomposition, at which we can arrive using a trivial extension to the discussion of the last section. The eigenvalue decomposition shows that a square matrix may be broken apart into the product of a matrix $V$, containing the eigenvectors of $A$ in its columns, a scaling (diagonal) matrix $A$, containing the eigenvalues of $A$, and the inverse of $V$. The general expression for the eigenvalue decomposition is shown below.
$$
A=V \cdot \Lambda \cdot \operatorname{inv}(V)
$$
The eigenvalue decomposition provides us with three benefits. As mentioned above, it breaks apart a sophisticated matrix into three simpler ones that provide a unique insight into the underlying transformation. Additionally, the only way to perform certain complicated matrix operations is to first compute the eigenvalue decomposition of $A$, perform the operation on $A$, and finally recompose the matrix. This sounds odd at first but becomes very clear as we proceed through this section. The third benefit is its invaluable assistance in computing the singular value decomposition, which by most accounts is one of the crown jewels of linear algebra.
电子代写|数字信号处理代写Digital Signal Processing代考|The Polar Decomposition
The polar decomposition breaks apart a real or complex valued matrix $A$ to produce a symmetric matrix $S$ and orthonormal matrix $O$. By itself, the polar decomposition does not see excessive use, but its derivation lays the ground work for the more illustrious singular value decomposition.
$$
A=O \cdot S
$$
The Singular Value Decomposition
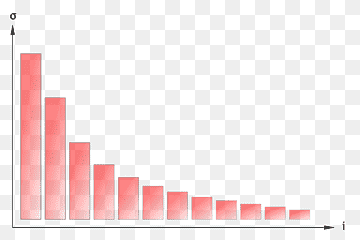
The singular value decomposition illustrates a rather unexpected and very useful result in linear algebra. It shows that any matrix $A$, whether real, complex, square, or rectangular, may be decomposed into an orthonormal matrix $U$, a diagonal matrix $\Sigma$ with real valued non-negative entries, and an additional orthonormal matrix $V$. The singular value decomposition, or SVD, is expressed as follows.
$$
A=U \cdot \Sigma \cdot V^T
$$
Recall that an orthonormal matrix causes a rotation, with a possible reflection, whereas the diagonal matrix represents a simple scaling transformation as we have seen in section 1.2.2.1. In a nutshell, the SVD claims that any matrix $A$ is at its core composed of a rotation/reflection, a real positive valued scaling transformation, followed by an additional rotation/reflection. The SVD finds use in many engineering applications, but in this text, we will use it to understand spatial multiplexing in MIMO antenna systems, which we discuss in the last chapter.
数字信号处理代写
电子代写|数字信号处理代写数字信号处理代考|矩阵分解
任何矩阵,无论是实值、复值方阵还是矩形阵,都可以分解成一定数量的更简单的矩阵,使我们更好地理解相关的变换。我们要研究的第一个分解是特征值分解,我们可以通过对上一节讨论的简单扩展来达到这一分解。特征值分解表明,一个方阵可以分解为一个矩阵$V$的乘积,其中在其列中包含$A$的特征向量,一个缩放(对角线)矩阵$A$,包含$A$的特征值,和$V$的逆。特征值分解的一般表达式如下所示。
$$
A=V \cdot \Lambda \cdot \operatorname{inv}(V)
$$
特征值分解为我们提供了三个好处。如上所述,它将一个复杂的矩阵分解为三个更简单的矩阵,提供对底层转换的独特洞察。另外,要进行某些复杂的矩阵运算,唯一的方法就是先计算$A$的特征值分解,再对$A$进行运算,最后重新组合矩阵。这一开始听起来很奇怪,但随着本节的深入,就变得非常清楚了。第三个好处是它在计算奇异值分解方面提供了宝贵的帮助,而奇异值分解在大多数情况下是线性代数的皇冠上的宝石之一
电子代写|数字信号处理代写数字信号处理代考|极坐标分解
极坐标分解分解实矩阵或复值矩阵 $A$ 生成一个对称矩阵 $S$ 还有标准正交矩阵 $O$。就其本身而言,极坐标分解并没有被过度使用,但它的推导为更杰出的奇异值分解奠定了基础$$
A=O \cdot S
$$奇异值分解说明了线性代数中一个相当出乎意料但非常有用的结果。它表明任何矩阵 $A$,无论是实、复、方或矩形,都可以分解为一个标准正交矩阵 $U$,一个对角矩阵 $\Sigma$ 实值非负项,和一个额外的标准正交矩阵 $V$。奇异值分解(SVD)表示为:
$$
A=U \cdot \Sigma \cdot V^T
$$回想一下,标准正交矩阵会引起旋转,并可能产生反射,而对角矩阵表示一个简单的缩放变换,如我们在1.2.2.1节中所见。简而言之,奇异值分解声称任何矩阵 $A$ 它的核心是由一个旋转/反射,一个实正值缩放变换,然后是一个附加的旋转/反射。SVD在许多工程应用中都有应用,但在本文中,我们将用它来理解MIMO天线系统中的空间多路复用,我们将在上一章中讨论这个问题

电子代写|数字信号处理代写Digital Signal Processing代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
微观经济学代写
微观经济学是主流经济学的一个分支,研究个人和企业在做出有关稀缺资源分配的决策时的行为以及这些个人和企业之间的相互作用。my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学Mathematics代写服务。我们的专家在图论代写Graph Theory代写方面经验极为丰富,各种图论代写Graph Theory相关的作业也就用不着 说。
线性代数代写
线性代数是数学的一个分支,涉及线性方程,如:线性图,如:以及它们在向量空间和通过矩阵的表示。线性代数是几乎所有数学领域的核心。
博弈论代写
现代博弈论始于约翰-冯-诺伊曼(John von Neumann)提出的两人零和博弈中的混合策略均衡的观点及其证明。冯-诺依曼的原始证明使用了关于连续映射到紧凑凸集的布劳威尔定点定理,这成为博弈论和数学经济学的标准方法。在他的论文之后,1944年,他与奥斯卡-莫根斯特恩(Oskar Morgenstern)共同撰写了《游戏和经济行为理论》一书,该书考虑了几个参与者的合作游戏。这本书的第二版提供了预期效用的公理理论,使数理统计学家和经济学家能够处理不确定性下的决策。
微积分代写
微积分,最初被称为无穷小微积分或 “无穷小的微积分”,是对连续变化的数学研究,就像几何学是对形状的研究,而代数是对算术运算的概括研究一样。
它有两个主要分支,微分和积分;微分涉及瞬时变化率和曲线的斜率,而积分涉及数量的累积,以及曲线下或曲线之间的面积。这两个分支通过微积分的基本定理相互联系,它们利用了无限序列和无限级数收敛到一个明确定义的极限的基本概念 。
计量经济学代写
什么是计量经济学?
计量经济学是统计学和数学模型的定量应用,使用数据来发展理论或测试经济学中的现有假设,并根据历史数据预测未来趋势。它对现实世界的数据进行统计试验,然后将结果与被测试的理论进行比较和对比。
根据你是对测试现有理论感兴趣,还是对利用现有数据在这些观察的基础上提出新的假设感兴趣,计量经济学可以细分为两大类:理论和应用。那些经常从事这种实践的人通常被称为计量经济学家。
Matlab代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。