如果你也在 怎样代写强化学习Reinforcement learning CS234这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。强化学习Reinforcement learning是机器学习的一个领域,涉及到智能代理应该如何在环境中采取行动,以使累积奖励的概念最大化。强化学习是三种基本的机器学习范式之一,与监督学习和无监督学习并列。
强化学习Reinforcement learning与监督学习的不同之处在于,不需要标记的输入/输出对,也不需要明确纠正次优的行动。相反,重点是在探索(未知领域)和利用(现有知识)之间找到平衡。部分监督RL算法可以结合监督和RL算法的优点。环境通常以马尔科夫决策过程(MDP)的形式陈述,因为许多强化学习算法在这种情况下使用动态编程技术。经典的动态编程方法和强化学习算法之间的主要区别是,后者不假定知道MDP的精确数学模型,它们针对的是精确方法变得不可行的大型MDP。
强化学习Reinforcement learning代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。最高质量的强化学习Reinforcement learning作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此强化学习Reinforcement learning作业代写的价格不固定。通常在专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
同学们在留学期间,都对各式各样的作业考试很是头疼,如果你无从下手,不如考虑my-assignmentexpert™!
my-assignmentexpert™提供最专业的一站式服务:Essay代写,Dissertation代写,Assignment代写,Paper代写,Proposal代写,Proposal代写,Literature Review代写,Online Course,Exam代考等等。my-assignmentexpert™专注为留学生提供Essay代写服务,拥有各个专业的博硕教师团队帮您代写,免费修改及辅导,保证成果完成的效率和质量。同时有多家检测平台帐号,包括Turnitin高级账户,检测论文不会留痕,写好后检测修改,放心可靠,经得起任何考验!
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
我们在计算机Quantum computer代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的计算机Quantum computer代写服务。我们的专家在机器学习Machine Learning代写方面经验极为丰富,各种机器学习Machine Learning相关的作业也就用不着 说。
CS代写|强化学习代写Reinforcement learning代考|Why Distributional Reinforcement Learning?
Just as a colour photograph conveys more information about a scene than a black and white photograph, the return distribution contains more information about the consequences of the agent’s decisions than the expected return. The expected return is a scalar, while the return distribution is infinite-dimensional; it is possible to compute the expectation of the return from its distribution, but not the other way around (to continue the analogy, one cannot recover hue from luminance).
By considering the return distribution, rather than just the expected return, we gain a fresh perspective on the fundamental problems of reinforcement learning. This includes understanding of how optimal decisions should be made, methods for creating effective representations of an agent’s state, and the consequences of interacting with other learning agents. In fact, many of the tools we develop here are useful beyond reinforcement learning and decision making. We call the process of computing return distributions distributional dynamic programming. Incremental algorithms for learning return distributions, such as quantile temporal-difference learning (Chapter 6) are likely to find uses wherever probabilities need to be estimated.
Throughout this book, we will encounter many examples in which we use the tools of distributional reinforcement learning to characterise the consequences of the agent’s choices. This is a modelling decision, rather than a reflection of some underlying truth about these examples. From a theoretical perspective, justifying our use of the distributional model requires us to make a number of probabilistic assumptions. These include the notion that the random nature of the interactions is intrinsically irreducible (what is sometimes called aleatoric uncertainty) and unchanging. As we encounter these examples, the reader is invited to reflect on these assumptions, and their effect on the learning process.
CS代写|强化学习代写Reinforcement learning代考|An Example: Kuhn Poker
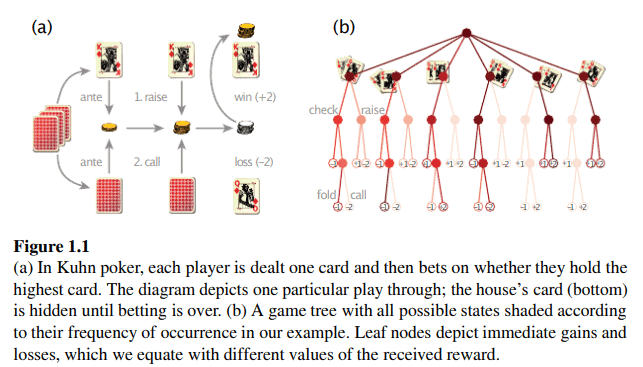
Kuhn poker is a simplified variant of the well-known card game. It is played with three cards of a single suit (jack, queen, and king) and over a single round of betting, as depicted in Figure 1.1a. Each player is dealt one card and must first bet a fixed ante, which for the purpose of this example we will take to be \$1. After looking at their card, the first player decides whether to raise, which doubles their bet, or check. In response to a raise, the second player can call and match the new bet or fold and lose their $\$ 1$ ante. If the first player chooses to check instead (keep the bet as-is), the option to raise is given to the second player, symmetrically. If neither player folded, the player with the higher card wins the pot ( $\$ 1$ or $\$ 2$, depending on whether the ante was raised). Figure $1.1 \mathrm{~b}$ visualises a single play of the game as a 55-state game tree.
Consider a player who begins with $\$ 10$ and plays a total of up to $T$ hands of Kuhn poker, stopping early if they go bankrupt or double their initial stake. To keep things simple, we assume that this player always goes first and that their opponent, the house, makes decisions uniformly at random. The player’s strategy depends on the card they are dealt, and also incorporates an element of randomness. There are two situations in which a choice must be made: whether to raise or check at first, and whether to call or fold when the other player raises. The following table of probabilities describes a concrete strategy as a function of the player’s dealt card:
\begin{tabular}{rccc}
Holding $a \ldots$ & Jack & Queen & King \
\hline Probability of raising & $1 / 3$ & 0 & 1 \
Probability of calling & 0 & $2 / 3$ & 1
\end{tabular}
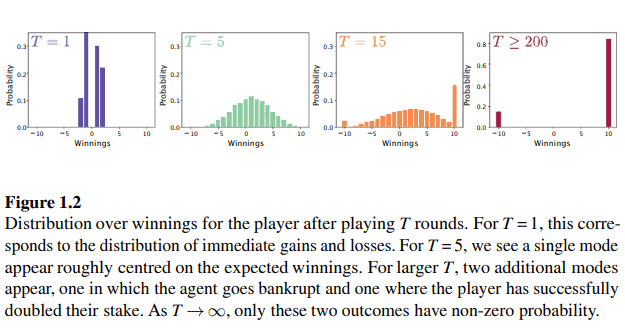
If we associate a positive and negative reward with each round’s gains or losses, then the agent’s random return corresponds to their total winnings at the end of the $T$ rounds, and ranges from $-10$ to 10 .
强化学习代写
CS代写|强化学习代写REINFORCEMENT LEARNING代考|WHY DISTRIBUTIONAL REINFORCEMENT LEARNING?
正如彩色照片比黑白照片传达更多关于场景的信息一样,返回分布包含的有关智能体决策后果的信息比预期返回更多。期望收益是一个标量,而收益分布是无限维 的;可以从其分布中计算回报的期望值,但反过来不行tocontinuetheanalogy, onecannotrecoverhuefromluminance.
通过考虑回报分布,而不仅仅是预期回报,我们对强化学习的其本问题有了新的认识。这包括了解应如何做出最佳决策、创建代理状态的有效表示的方法以及与其 他学习代理交互的后果。事实上,我们在这里开发的许多工具在强化学习和决策之外都非常有用。我们将计算回报分布的过程称为分布动态规划。用于学习回报分 布的增量算法,例如分位数时差学习Chapter6很可能在需要估计概率的地方找到用途。
在本书中,我们会遇到很多例子,在这些例子中,我们使用分布式强化学习工具来描述智能体选择的后果。这是一个建模决策,而不是反映有关这些示例的一些基 本事实。从理论的角度来看,证明我们使用分布模型的合理性需要我们做出一些概率假设。这些包括相互作用的随机性本质上是不可约的概念 whatissometimescalledaleatoricuncertainty并且不变。当我们遇到这些例子时,请读者反思这些假设,以及它们对学习过程的影响。
CS代写|强化学习代写REINFORCEMENT LEARNING代考|AN EXAMPLE: KUHN POKER
库恩扑克是著名纸牌游戏的简化变体。它是用三张单一花色的牌来玩的jack, queen, andking以及单轮投注,如图 1.1a所示。每个玩家都发一张牌,并且必须首 先下注一个固定的底注,在本例中我们将其设为 1 美元。在亱看他们的牌后,第一个玩家决定是加注,这使他们的赌注翻倍,还是过牌. 响应加注,第二个玩家可以 跟注并匹配新的赌注或弃牌并输掉他们的赌注。\$1赌注。如果第一个玩家选择过牌keepthebetas-is, 加注的选项对称地给予第二位玩家。如果两个玩家都没有 弃牌,则拥有较高牌的玩家嬴得底池\$\$1\$or\$\$2\$, dependingonwhethertheantewastaised. 数字 $1.1$ b将游戏的单个游戏可视化为 55 个状态的游戏树。
考虑一个以 $\$ 10$ 总共播放多达 $T$ Kuhn 扑克的手,如果他们破产或将初始本金加倍,就会提前停止。为简单起见,我们假设该玩家总是先走,而他们的对手,即庄 家,随机统一地做出决定。玩家的策略取决于发给他们的牌,并且还包含随机性元表。有两种情况必须做出选择:首先是加注还是过牌,以及当其他玩家加注时是 跟注还是弃牌。下面的概率表描述了作为玩家发牌函数的具体策略:
如果我们将正奖励和负奖励与每一轮的收益或损失联系起来,那么代理的随机回报对应于他们在回合结束时的总收益 $T$ 轮次,范围从-10到 10 。

CS代写|强化学习代写Reinforcement learning代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
微观经济学代写
微观经济学是主流经济学的一个分支,研究个人和企业在做出有关稀缺资源分配的决策时的行为以及这些个人和企业之间的相互作用。my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学Mathematics代写服务。我们的专家在图论代写Graph Theory代写方面经验极为丰富,各种图论代写Graph Theory相关的作业也就用不着 说。
线性代数代写
线性代数是数学的一个分支,涉及线性方程,如:线性图,如:以及它们在向量空间和通过矩阵的表示。线性代数是几乎所有数学领域的核心。
博弈论代写
现代博弈论始于约翰-冯-诺伊曼(John von Neumann)提出的两人零和博弈中的混合策略均衡的观点及其证明。冯-诺依曼的原始证明使用了关于连续映射到紧凑凸集的布劳威尔定点定理,这成为博弈论和数学经济学的标准方法。在他的论文之后,1944年,他与奥斯卡-莫根斯特恩(Oskar Morgenstern)共同撰写了《游戏和经济行为理论》一书,该书考虑了几个参与者的合作游戏。这本书的第二版提供了预期效用的公理理论,使数理统计学家和经济学家能够处理不确定性下的决策。
微积分代写
微积分,最初被称为无穷小微积分或 “无穷小的微积分”,是对连续变化的数学研究,就像几何学是对形状的研究,而代数是对算术运算的概括研究一样。
它有两个主要分支,微分和积分;微分涉及瞬时变化率和曲线的斜率,而积分涉及数量的累积,以及曲线下或曲线之间的面积。这两个分支通过微积分的基本定理相互联系,它们利用了无限序列和无限级数收敛到一个明确定义的极限的基本概念 。
计量经济学代写
什么是计量经济学?
计量经济学是统计学和数学模型的定量应用,使用数据来发展理论或测试经济学中的现有假设,并根据历史数据预测未来趋势。它对现实世界的数据进行统计试验,然后将结果与被测试的理论进行比较和对比。
根据你是对测试现有理论感兴趣,还是对利用现有数据在这些观察的基础上提出新的假设感兴趣,计量经济学可以细分为两大类:理论和应用。那些经常从事这种实践的人通常被称为计量经济学家。
Matlab代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。



