如果你也在 怎样代写微观经济学Microeconomics ECON1001这个学科遇到相关的难题，请随时右上角联系我们的24/7代写客服。微观经济学Microeconomics是主流经济学的一个分支，研究个人和公司在做出有关稀缺资源分配的决策时的行为以及这些个人和公司之间的互动。微观经济学侧重于研究单个市场、部门或行业，而不是宏观经济学所研究的整个国民经济。

微观经济学Microeconomic的一个目标是分析在商品和服务之间建立相对价格的市场机制，并在各种用途之间分配有限资源。微观经济学显示了自由市场导致理想分配的条件。它还分析了市场失灵，即市场未能产生有效的结果。微观经济学关注公司和个人，而宏观经济学则关注经济活动的总和，处理增长、通货膨胀和失业问题以及与这些问题有关的国家政策。微观经济学还处理经济政策（如改变税收水平）对微观经济行为的影响，从而对经济的上述方面产生影响。

同学们在留学期间，都对各式各样的作业考试很是头疼，如果你无从下手，不如考虑my-assignmentexpert™！

my-assignmentexpert™提供最专业的一站式服务：Essay代写，Dissertation代写，Assignment代写，Paper代写，Proposal代写，Proposal代写，Literature Review代写，Online Course，Exam代考等等。my-assignmentexpert™专注为留学生提供Essay代写服务，拥有各个专业的博硕教师团队帮您代写，免费修改及辅导，保证成果完成的效率和质量。同时有多家检测平台帐号，包括Turnitin高级账户，检测论文不会留痕，写好后检测修改，放心可靠，经得起任何考验！

想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。

我们在经济Economy代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的经济Economy代写服务。我们的专家在微观经济学Microeconomics代写方面经验极为丰富，各种微观经济学Microeconomics相关的作业也就用不着 说。

经济代写|微观经济学代考Microeconomics代写|Models of decision under bounded rationality

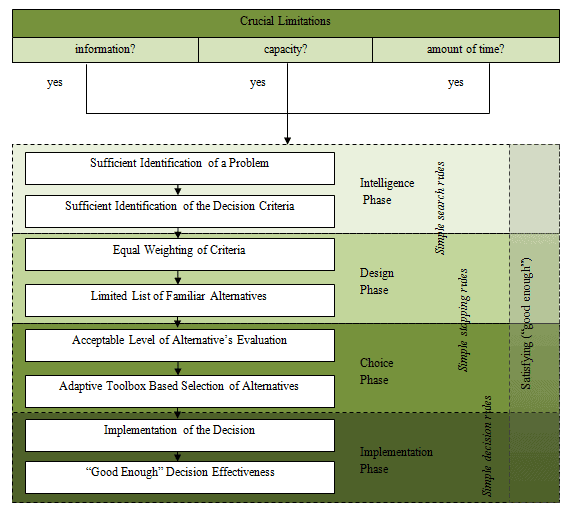
A first model of choice under bounded rationality is the “satisficing model” proposed by Simon (1982) in opposition to the classic “optimizing” model. The decision-maker judges actions by means of partial criteria $u_k$, to which are attributed the aspiration thresholds $\sigma_k$; he examines the actions in a predefined order and chooses the first one to attain the aspiration thresholds for all the criteria: $s_i$ such that $u_k\left(s_i\right) \geq \sigma_k$. As a particular case, one can consider a unique criterion $u$ (as in the case of optimisation), with its aspiration threshhold $\varepsilon$; the decision-maker chooses the action $s_i$ such that $u\left(s_i\right) \geq \sigma$. At first sight, the $\varepsilon$-rationality model of Radner fits this definition, by considering that the decision-maker chooses the first action that approaches to within $\varepsilon$ of the optimum: $u\left(s_i\right) \geq \max _i u\left(s_i\right)-\varepsilon$, but here the aspiration threshold actually depends on the maximum attainable utility, which is generally unknown to the decision-maker. It can be observed that the satisficing model admits the optimizing model as limiting case when the aspiration thresholds are high enough. However, the satisficing model is directly expressed in terms of bounded instrumental rationality and not bounded cognitive rationality. For this latter to appear, we must examine a process of deliberation by the decision-maker that brings into play cognitive constraints such that he is led to seek a satisfactory action. Such a process, which would have the advantage of endogenising the aspiration thresholds of the decision-maker, has not yet been proposed.
A second model of choice under limited rationality is the “probabilist choice model” (Anderson, de Palma, Thisse, 1992). From a finite set of possible actions, the decision maker chooses the action $i$ with probability $p_i$ such that: $p_i=w_i / \sum_j w_j$, where $w_i$ is a propensity to choose the action $i$ linked to an index of utility $u_i$ of the action $i$. In the linear model, the parameters $w_i$ are proportional to the index of utility: $w_i=u_i$. In the multinomial logit model, the parameters $w_i$ are written in exponential form: $w_i=e^{\mu u_i}$, with the convenient introduction of a parameter $\mu$. Here again, the logit model converges towards the optimising model when the parameter $\mu$ tends to infinity; the decision-maker acts then no more in a stochastic manner, but in a determinist manner (except in the case of indifference between two actions). Conversely, the logit model tends to a purely random choice model when $\mu$ tends to zero. The parameter $\mu$ thus appears to reflect the limited cognitive capacities of the decision maker, but yet again it operates in a model expressing limited instrumental rationality. However, two cognitive justifications of this model, endogenising the parameter $\mu$, have been put forward. In the first, the decision-maker is endowed with a random utility function, but remains optimising to such an extent that he implements each action with the probability that it is the optimising one. When the law of probability of the utility is chosen correctly (doubly exponential), the logit model is obtained. In the second justification (Mattsson-Weibull, 2002), the decision-maker chooses an action by arbitrating between its utility and a control cost in relation to a reference action. When the control cost is chosen correctly (in the form of entropy), the logit model is again obtained.

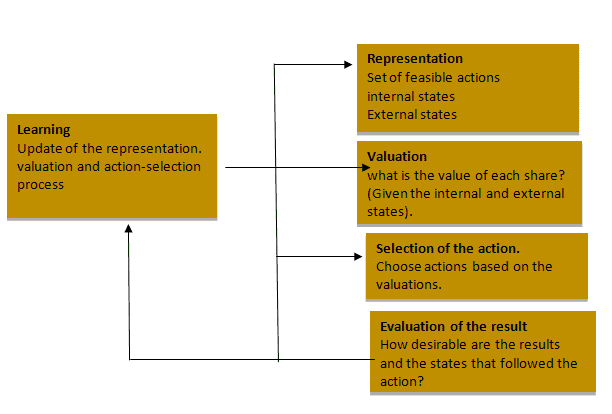
经济代写|微观经济学代考Microeconomics代写|Models of learning in static situations

The “fictitious play model” assumes that the decision-maker, during a repeated process of decision, is capable of predicting the future states of nature. Moreover, this model essentially expresses exploitation behavior. The decision-maker observes the past frequency of states of nature, deduces from it a distribution of probabilities on future states and chooses, for each period, the action which maximises his expected utility according to this distribution. Exploration behavior can be introduced through voluntary deviation from the above behavior, and this deviation can take two forms. In the ” $\varepsilon$-greedy fictitious play” model, the decision maker can either use the optimum action with the probability $1-\varepsilon$, or use another action drawn uniformly at random with the probability $\varepsilon$. In the “disturbed fictitious play” model, the decision-maker uses the logit (and no longer optimising) choice rule with, as index of utility, the expected utility calculated for each action. For the standard fictitious play, one can easily demonstrate that the decision process will converge towards the optimal action (in the sense of maximisation of expected utility) simply by means of the law of large numbers (the frequency of appearance of each state tends to its probability). For the variations proposed, on the contrary, this convergence is not sure because the random component generated by exploration does not disappear asymptotically.

The “CPR model” (Laslier-Topol-Walliser, 2000) is a model of reinforcement (Roth-Erev, 1995) which assumes that the decision-maker only observes the past performance of his actions and no longer observes the states of nature. It considers that the decision-maker adopts, as index of utility, the cumulative utility obtained for each action and that he chooses his future action with a probability proportional to this index. This model presents good properties as regards the exploration-exploitation dilemma. At the beginning of the process, as the indexes are often initialised uniformly, the decision-maker carries out a systematic exploration of all the actions. At the end of the process, if the index of one action becomes predominant in relation to the others, exploitation becomes very strong, although exploration is never abandoned (every action possesses a residual probability of being chosen). What is more, if one increases (decreases) the parameter $\mu$, one moves the exploration-exploitation compromise towards more exploitation (exploration). For $\mu=0$, there is pure exploration because all the actions are used with the same probability; for $\mu=\infty$, there is pure exploitation because only the action with the maximum index of utility is used. It can be demonstrated that the learning process thus defined converges towards the optimal action (still in the sense of expected utility) because the good actions are played more and more often, due to a retroactive effect of the cumulative utility, whereas exploration tends to zero.

微观经济学代写

经济代写|微观经济学代考MICROECONOMICS代写|MODELS OF DECISION UNDER BOUNDED RATIONALITY

有限理性下的第一个选择模型是西蒙提出的“满意模型”1982与经典的“优化”模型相反。决策者通过部分标准来判断行动 $u_k$, 归因于吸入嘓值 $\sigma_k$; 他按照预定义的顾 序检育动作，并选择第一个达到所有标准的期望阈值的动作: $s_i$ 这样 $u_k\left(s_i\right) \geq \sigma_k$. 作为一种特殊情况，可以考虑一个独特的标准 $u$ asinthecaseofoptimisation, 及其吸入阈值 $\varepsilon$; 决策者选择行动 $s_i$ 这样 $u\left(s_i\right) \geq \sigma$. 乍一看， $\varepsilon$-Radner 的理性模型符合这个定义，考虑到决策者选择接近内部的第一个行动 $\varepsilon$ 最佳的：
$u\left(s_i\right) \geq \max _i u\left(s_i\right)-\varepsilon$ ，但这里的期望阈值实际上取决于最大可达到的效用，这通常是决策者不知道的。可以观察到，当期望阈值足够高时，满足模型将优化 模型视为极限情况。然而，懑足模型直接用有限的工具理性而不是有限的认知理性来表达。对于后者的出现，我们必须检䝺决策者的深思孰虑过程，该过程使认知 约束发挥作用，从而导致他寻求令人满意的行动。尚末提出这样一个过程，它具有使决策者的愿望阈值内生化的优势。
有限理性下的第二种选择模型是“概率选择模型”Anderson, dePalma, Thisse, 1992. 从一组有限的可能行动中，决策者选择行动 $i$ 有概率 $p_i$ 这样:
$p_i=w_i / \sum_j w_j$ ， 在哪里 $w_i$ 是选择行动的倾向 $i$ 与效用指数挂钧 $u_i$ 行动的 $i$. 在线性模型中，参数 $w_i$ 与效用指数成正比: $w_i=u_i$. 在多项式logit模型中，参数 $w_i$ 写 成指数形式: $w_i=e^{\mu u_i}$, 方便地引入一个参数 $\mu$. 同样，当参数 $\mu$ 趋于无穷大; 决策者不再以随机方式行事，而是以确定性方式行事
exceptinthecaseofindifferencebetweentwoactions. 相反， logit 模型在以下情况下趋向于纯随机选择模型 $\mu$ 趋于零。参数 $\mu$ 因此似乎反映了决策者有限的认知 能力，但它又一次在表达有限工具理性的模型中运作。然而，这个模型的两个认知理由，内生参数 $\mu$ ，提出来了。在第一种情况下，决策者被赋予了一个随机的效 用函数，但仍保持优化到这样的程度，即他执行每个动作的概率都是优化的。当效用概率定律选择正确时doublyexponential，得到logit模型。在第二个理由 Mattsson – Weibull, 2002，决策者通过在其效用和与参考行动相关的控制成本之间进行仲裁来选择行动。正确选择控制成本时intheformofentropy，再次 得到logit模型。

经济代写|微观经济学代考MICROECONOMICS代写|MODELS OF LEARNING IN STATIC SITUATIONS

“虚拟游戏模型”假设决策者在重晶决策过程中能够预测末来的自然状态。此外，该模型本质上表达了剥削行为。决策者观察过去的自然状态频率，从中推导出末来 状态的概率分布，并根据该分布为每个时期选择最大化其预期效用的行动。可以通过自愿偏离上述行为来引入探索行为，这种偏离可以有两种形式。在里面 ” $\varepsilon-$ greedy fictitious play”模型，决策者可以使用概率为 $1-\varepsilon$ ，或者使用另一个随机抽取的动作，概率为 $\varepsilon$. 在 “被打扰的虚拟游戏”模型中，决策者使用logit andnolongeroptimising选择规则，作为效用指标，为每个动作计算的预期效用。对于标准的虚构游戏，可以很容易地证明决策过程将收敛于最佳行动 inthesenseofmaximisationofexpectedutility仅仅通过大数定律 the frequencyofappearanceofeachstatetendstoitsprobability. 相反，对于提出的变 体，这种收敛是不确定的，因为探索产生的随机成分不会渐近消失。
“心肺复苏模型” Laslier – Topol – Walliser, 2000是强化模型Roth – Erev, 1995它假定决策者只观崇其行为的过去表现，而不再观察自然状态。它认为决策 者采用每次行动所获得的甸积效用作为效用指标，并以与该指标成正比的概率选择末来的行动。该模型在探索-开发困境方面表现出良好的特性。在过程开始时， 由于指标往往是统一初始化的，决策者对所有的动作进行系统的探索。在这个过程的最后，如果一个行动的指标相对于其他行动变得占主导地位，那么剥削就会变 得非常强烈，尽管探索永远不会被放弃everyactionpossessesaresidualprobabilityofbeingchosen. 更重要的是，如果一个增加decreases参数 $\mu$ ，一个人将勘 探-开发折䖵方䓌转向更多的开发exploration. 为了 $\mu=0$ ，存在纯糉的探索，因为所有的动作都以相同的概率被使用；为了 $\mu=\infty$ ，存在纯粹的剥削，因为只使 用具有最大效用指数的动作。可以证明，如此定义的学习过程收敛于最佳动作stillinthesenseofexpectedutility因为由于甸积效用的追溯效应，好的行为被玩得 越来越频筦，而探索趋于零。

经济代写|微观经济学代考Microeconomics代写 请认准exambang™. exambang™为您的留学生涯保驾护航。

微观经济学代写

微观经济学是主流经济学的一个分支，研究个人和企业在做出有关稀缺资源分配的决策时的行为以及这些个人和企业之间的相互作用。my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学Mathematics代写服务。我们的专家在图论代写Graph Theory代写方面经验极为丰富，各种图论代写Graph Theory相关的作业也就用不着 说。

线性代数代写

线性代数是数学的一个分支，涉及线性方程，如：线性图，如：以及它们在向量空间和通过矩阵的表示。线性代数是几乎所有数学领域的核心。

博弈论代写

现代博弈论始于约翰-冯-诺伊曼（John von Neumann）提出的两人零和博弈中的混合策略均衡的观点及其证明。冯-诺依曼的原始证明使用了关于连续映射到紧凑凸集的布劳威尔定点定理，这成为博弈论和数学经济学的标准方法。在他的论文之后，1944年，他与奥斯卡-莫根斯特恩（Oskar Morgenstern）共同撰写了《游戏和经济行为理论》一书，该书考虑了几个参与者的合作游戏。这本书的第二版提供了预期效用的公理理论，使数理统计学家和经济学家能够处理不确定性下的决策。

微积分代写

微积分，最初被称为无穷小微积分或 “无穷小的微积分”，是对连续变化的数学研究，就像几何学是对形状的研究，而代数是对算术运算的概括研究一样。

它有两个主要分支，微分和积分；微分涉及瞬时变化率和曲线的斜率，而积分涉及数量的累积，以及曲线下或曲线之间的面积。这两个分支通过微积分的基本定理相互联系，它们利用了无限序列和无限级数收敛到一个明确定义的极限的基本概念 。

计量经济学代写

什么是计量经济学？
计量经济学是统计学和数学模型的定量应用，使用数据来发展理论或测试经济学中的现有假设，并根据历史数据预测未来趋势。它对现实世界的数据进行统计试验，然后将结果与被测试的理论进行比较和对比。

根据你是对测试现有理论感兴趣，还是对利用现有数据在这些观察的基础上提出新的假设感兴趣，计量经济学可以细分为两大类：理论和应用。那些经常从事这种实践的人通常被称为计量经济学家。

Matlab代写

MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中，其中问题和解决方案以熟悉的数学符号表示。典型用途包括：数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发，包括图形用户界面构建MATLAB 是一个交互式系统，其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题，尤其是那些具有矩阵和向量公式的问题，而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问，这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展，得到了许多用户的投入。在大学环境中，它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域，MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要，工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数（M 文件）的综合集合，可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。