如果你也在 怎样代写有限元方法finite differences method ENGR7961这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。有限元方法finite differences method在数值分析中,是一类通过用有限差分逼近导数解决微分方程的数值技术。空间域和时间间隔(如果适用)都被离散化,或被分成有限的步骤,通过解决包含有限差分和附近点的数值的代数方程来逼近这些离散点的解的数值。
有限元方法finite differences method有限差分法将可能是非线性的常微分方程(ODE)或偏微分方程(PDE)转换成可以用矩阵代数技术解决的线性方程系统。现代计算机可以有效地进行这些线性代数计算,再加上其相对容易实现,使得FDM在现代数值分析中得到了广泛的应用。今天,FDM与有限元方法一样,是数值解决PDE的最常用方法之一。
有限元方法finite differences method作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。 最高质量的有限元方法finite differences method作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此有限元方法finite differences method作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
同学们在留学期间,都对各式各样的作业考试很是头疼,如果你无从下手,不如考虑my-assignmentexpert™!
my-assignmentexpert™提供最专业的一站式服务:Essay代写,Dissertation代写,Assignment代写,Paper代写,Proposal代写,Proposal代写,Literature Review代写,Online Course,Exam代考等等。my-assignmentexpert™专注为留学生提供Essay代写服务,拥有各个专业的博硕教师团队帮您代写,免费修改及辅导,保证成果完成的效率和质量。同时有多家检测平台帐号,包括Turnitin高级账户,检测论文不会留痕,写好后检测修改,放心可靠,经得起任何考验!
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
我们在数学Mathematics代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学Mathematics代写服务。我们的专家在微积分Calculus Assignment代写方面经验极为丰富,各种微积分Calculus Assignment相关的作业也就用不着 说。
数学代写|有限元方法作业代写finite differences method代考|FEM FOR TWO-DIMENSIONAL SOLIDS
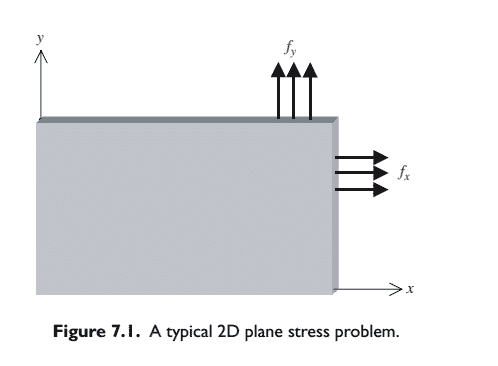
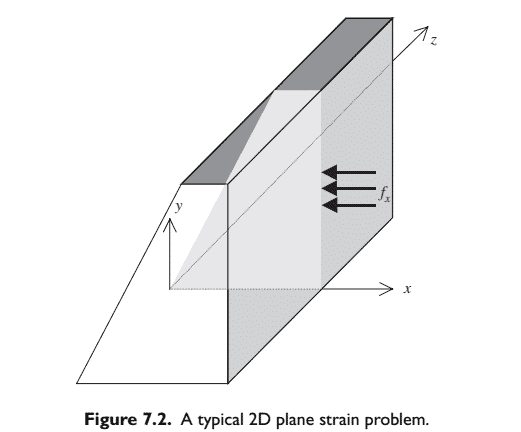
In this chapter, we develop, in an easy to understand manner, finite element equations for the stress analysis of two-dimensional (2D) solids subjected to external loads. The basic concepts, procedures and formulations can also be found in many existing textbooks (see, e.g. Zienkiewicz and Taylor, 2000). The element developed is called a 2D solid element that is used for structural problems where the loading-and hence the deformation-occur within a plane. Though no real life structure can be truly $2 \mathrm{D}$, experienced analysts can often idealize many practical problems to $2 \mathrm{D}$ problems to obtain satisfactory results by carrying out analyses using 2D models, which can be very much more efficient and cost-effective compared to conducting full 3D analyses. In engineering applications, there are ample practical problems that can be modelled as 2D problems. As discussed in Chapter 2, there are plane stress and plane strain problems, whereby correspondingly, plane stress and plane strain elements need to be used to solve them. For example, if we have a plate structure with loading acting in the plane of the plate as in Figure 7.1, we need to use 2D plane stress elements. When we want to model the effects of water pressure on a dam, as shown in Figure 7.2, we have to use 2D plane strain elements.
Note that in Figure 7.1, plane stress conditions are usually applied to structures that have a relatively small thickness as compared to its other dimensions. Due to the absence of any off-plane external force, the normal stresses are negligible, which leads to a plane stress situation. In cases where plane strain conditions are applied, as in Figure 7.2, the thickness of the structure (in the $z$ direction) is relatively large as compared to its other dimensions, and the loading (pressure) is uniform along the elongated direction. The deformation is, therefore, approximated to be the same throughout its thickness. In this case, the off-plane strain (strain components in the $z$ direction) is negligible, which leads to a plane strain situation. In either a plane stress or plane strain situation, the governing system equation can be drastically simplified, as shown in Chapter 2 . The formulations for plane stress and plane strain problems are very much the same, except for the difference in the material constant matrix.
数学代写|有限元方法作业代写finite differences method代考|LINEAR TRIANGULAR ELEMENTS
The linear triangular element was the first type of element developed for 2D solids. The formulation is also the simplest among all the 2D solid elements. It has been found that the linear triangular element is less accurate compared to linear quadrilateral elements. For this reason, it is often thought to be ideal to use quadrilateral elements, but the reality is that the triangular element is still a very useful element for its adaptivity to complex geometry. Triangular elements are normally used when we want to mesh a $2 \mathrm{D}$ model involving complex geometry with acute corners. In addition, the triangular configuration with the simplest topological feature makes it easier to develop meshing processors. Nowadays, analysts are hoping to use a fully automated mesh generator to perform the complex task of analysis that needs repeated or even adaptive re-meshing. Most automated mesh generators can only create triangular elements. There are automated mesh generators that can generate a quadrilateral mesh, but they still use triangular elements as patches for difficult situations, and end up with a mesh of mixed elements. Hence, whether we like it or not, we still have to use triangular elements for many practical engineering problems.
Consider a 2D model in the $x-y$ plane, shown schematically in Figure 7.3. The 2D domain is divided in a proper manner into a number of triangular elements. The ‘proper’ meshing of a domain will be outlined in Chapter 11 , where a list of guidelines is provided. In a mesh of linear triangular elements, each triangular element has three nodes and three straight edges.
有限元方法代写
数学代写|有限元方法作业代写FINITE DIFFERENCES METHOD代考|FEM FOR TWO-DIMENSIONAL SOLIDS
在本章中,我们以易于理解的方式开发了用于二维应力分析的有限元方程。 $2 D$ 承受外傤荷的固体。基本概、程序和公式也可以在许多现有教
在平面应力和平面应变问题, 相应地,需要使用平面应力和平面应变单元来求解它们。例如,如果我们不一个板结构,如图 7.1.所示,载荷作用在
板的平面上,我们需要使用 $2 D$ 平面应力单元。 当我们想要模拟水压对大坝的影㕷时,如图 7.2 所示,我们必须使用 $2 D$ 平面应变单元
似,只是材料常数矩阵不同。
数学代写|有限元方法作业代写FINITE DIFFERENCES METHOD代考|LINEAR TRIANGULAR ELEMENTS
线性三角形单元是为二维实体开发的第一种单元。该公式也是所有二维实体单元中最简单的。已经发现,与线性四边形元素相比,线性三角形元 責不太准确。出于这个原因,通常认为使用四边形单元是理想的,但实际情况是三角形单元仍然是一个非常有用的单元,因为它对复杂的几何形 状具有适应性。当我们想要对一个网格进行网格化时,通常使用三角形单元 $2 D$ 涉及具有锐角的复杂几何体的模型。此外,具有最简单拓扑特征的
三角形配置使网格处理器的开发变得更加容易。如今,分析师希望使用全自动网格生成器来执行需要重复甚至自适应重新网格化的复杂分析任
务。大多数自动网格生成器只能创建三角形元素。有可以生成四边形网格的自动网格生成器,但它们仍然使用三角形元素作为困难情况的补丁
并最终得到混合元素的网格。因此,不
考虑一个二维模型 $x-y$ 平面,如图 7.3 所示。一维域以适当的方式划分为多个三角形元素。域的“适当”网格划分将在第 11 章中概述,其中提供了
一系列指南。在线性三角形单元的网格中,每个三角形单元具有三个节点和三个直边。

数学代写|有限元方法作业代写finite differences method代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。

