数学代写|CS167 Cryptography

MY-ASSIGNMENTEXPERT™可以为您提供 ics.uci.edu CS167 Cryptography密码学的代写代考和辅导服务！

CS167课程简介

Announcement(s):
Monday, January 21, No class, Martin Luther King Jr. Day (no office hours on the following Tuesday either).
Midterm Exam 1: Friday, February 8, 2008, in class.
Reading: Trappe-Washington, Chapters 1-6.
Monday, February 18, No class, Presidents Day
Midterm Exam 2: Friday, February 29, 2008, in class.
Reading: Trappe-Washington, Chapters 7-9.
Final Exam: 8:00am – 10:00am, Wednesday, March 19, 2008.
Reading: previous readings plus Trappe-Washington, Chapters 10,12-14.

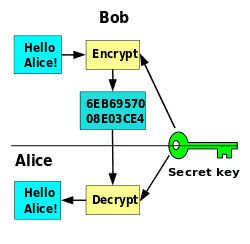
This course explains the inner working of cryptographic tools, the security properties they are designed to achieve, how to reason about their security, and how to properly use them. We will cover topics such as encryption (secret-key and public-key), message authentication, user authentication, digital signatures, key management, cryptographic hashing, network security protocols (SSL, IPsec), and public-key infrastructure. Towards the end of the class we will touch on a few advanced topics such as zero-knowledge proofs and secure computation.

Prerequisites 

Prerequisites: The course is intended for upper-level undergraduates, and we assume familiarity with algorithms (CS.161) and discrete math (ICS.6B / ICS.6D). Basic understanding of probability theory and modular arithmetic will be helpful, although we will review relevant concepts as we need them.

Object
To test understanding of I/O (input output) functions for file handling, and to use the bitwise operators.

Task description
This program consists of two parts: encryption of a file, and decryption of a file that has been previously encrypted. Encryption is the process of rendering a text file unreadable by humans, yet by applying the process in reverse (decryption) the file can be recovered in its original state.

CS167 Cryptography HELP（EXAM HELP， ONLINE TUTOR）

A shift cipher is a type of substitution cipher where each letter in the plaintext is shifted a certain number of places down the alphabet. In a shift cipher with a key $k=5$, each letter is shifted 5 places down the alphabet.

To encrypt the plaintext “ATTACKATDAWN” using a shift cipher with $k=5$, we can shift each letter in the plaintext by 5 positions to get the corresponding letter in the ciphertext.

Here’s how it works:

Plaintext: A T T A C K A T D A W N Shift key: 5 5 5 5 5 5 5 5 5 5 5 5 Ciphertext: F Y Y F H P F Y I F B S

Therefore, the ciphertext for “ATTACKATDAWN” using a shift cipher with shift key $k=5$ is “FYYFHPUFYIFBS”.

ROT13 is a simple shift cipher that shifts each letter in the plaintext by 13 positions down the alphabet. When it is applied twice, it returns the original plaintext because shifting each letter by 13 positions twice is equivalent to shifting it by 26 positions, which brings the letter back to its original position. This property of ROT13 is possible because 13 is half of 26, the number of letters in the English alphabet.

However, there is no single shift cipher for English text such that when it is applied three times it returns the original plaintext. This is because the number of possible keys for a shift cipher is limited to 25 (not including the identity permutation where the plaintext is the same as the ciphertext), since a shift by 26 positions would bring the letter back to its original position, and any shift by more than 26 positions can be reduced to a shift by a smaller number of positions. Since the greatest common divisor of 26 and any number less than 26 is 1, applying a shift cipher multiple times will never return the original plaintext for any number of shifts greater than 2.

An example of a simple shift cipher for English other than ROT13 such that when it is applied some number $m<26$ times it returns the original plaintext is a shift cipher with a key $k=7$. This means that each letter in the plaintext is shifted 7 positions down the alphabet. To show that this cipher returns the original plaintext when applied 13 times, we can calculate:

• The first shift encrypts the plaintext as follows:Plaintext: A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Ciphertext: H I J K L M N O P Q R S T U V W X Y Z A B C D E F G
• The second shift encrypts the ciphertext as follows:Plaintext: H I J K L M N O P Q R S T U V W X Y Z A B C D E F G Ciphertext: O P Q R S T U V W X Y Z A B C D E F G H I J K L M N
• Continuing this process 11 more times, we get:Plaintext: A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Ciphertext: A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Therefore, the value of $m$ for this cipher is 13, since the original plaintext is obtained after 13 shifts.

MY-ASSIGNMENTEXPERT™可以为您提供UNIVERSITY OF ILLINOIS URBANA-CHAMPAIGN MATH2940 linear algebra线性代数课程的代写代考和辅导服务！ 请认准MY-ASSIGNMENTEXPERT™. MY-ASSIGNMENTEXPERT™为您的留学生涯保驾护航。