如果你也在 怎样代写核物理Nuclear Physics PHYS5011这个学科遇到相关的难题，请随时右上角联系我们的24/7代写客服。核物理Nuclear Physics是研究原子核及其成分和相互作用的物理学领域，此外还研究其他形式的核物质。核物理学不应与原子物理学相混淆，后者研究原子的整体，包括其电子。

核物理Nuclear Physics的发现已经导致了许多领域的应用。这包括核能、核武器、核医学和磁共振成像、工业和农业同位素、材料工程中的离子植入，以及地质学和考古学中的放射性碳测定。此类应用在核工程领域进行研究。粒子物理学是从核物理学中发展出来的，这两个领域通常是紧密联系在一起进行教学。核天体物理学，即核物理学在天体物理学中的应用，对于解释恒星的内部运作和化学元素的起源至关重要。

同学们在留学期间，都对各式各样的作业考试很是头疼，如果你无从下手，不如考虑my-assignmentexpert™！

my-assignmentexpert™提供最专业的一站式服务：Essay代写，Dissertation代写，Assignment代写，Paper代写，Proposal代写，Proposal代写，Literature Review代写，Online Course，Exam代考等等。my-assignmentexpert™专注为留学生提供Essay代写服务，拥有各个专业的博硕教师团队帮您代写，免费修改及辅导，保证成果完成的效率和质量。同时有多家检测平台帐号，包括Turnitin高级账户，检测论文不会留痕，写好后检测修改，放心可靠，经得起任何考验！

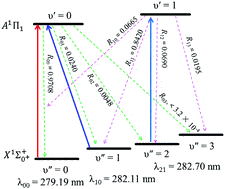
物理代写|核物理代考Nuclear Physics代写|Lifetimes and branching ratios

In eqn 2.90 , the only term that changes after a Lorentz transformation is $E_a$ and the decay rate transforms as:
$$
\Gamma_{i \rightarrow f}^{\prime}=\Gamma_{i \rightarrow f} / \gamma
$$
An observer in the laboratory frame sees, for example, a muon decaying slower than in CM. Since a muon always decays in $e^{-} \nu_\mu \bar{\nu}_e$, its lifetime is simply $\Gamma^{-1}$. This is a consequence of quantum mechanics: for a system of $N$ particles in the same unstable state, the number of particles that reach the ground state in $d t$ is $d N=-N \Gamma d t$. The minus sign indicates that the number of unstable particles decreases with time and the number of particles in the ground state increases. The unstable particles that survive after a time $t$ is then:
$$
N(t)=N(0) e^{-\Gamma t} .
$$

物理代写|核物理代考Nuclear Physics代写|Unstable states

Even if non-relativistic quantum mechanics is unable to describe the creation and annihilation of particles (Bromberg, 1976), it is equipped with a formalism to describe unstable states. The probability of finding an unstable particle in space decreases with time and the wavefunction fades away as:
$$
|\psi(\mathbf{x}, t)|^2=|\psi(\mathbf{x}, 0)|^2 e^{-t / \tau} .
$$
The damping term is an exponential function compatible with the decay law of eqn 2.95. The stationary states of the Schrödinger equation are no more:
$$
\psi(\mathbf{x}, t)=\psi(\mathbf{x}) e^{-i E t}
$$
but are replaced by states vanishing for $t \rightarrow+\infty$ :
$$
\psi(\mathbf{x}, t)=\psi(\mathbf{x}) e^{-i E t} e^{-t / 2 \tau} .
$$
A vanishing state is not a stationary state and its disappearance at large times brings subtle QM effects. Due to the Heisenberg uncertainty principle of Sec. B.4, the energy of the stationary state can be measured with arbitrary precision provided that $\Delta E \Delta t \geq \hbar / 2$ or (in NU) $\Delta E \geq 1 /(2 \Delta t)$. If the particle does not endure the passage of time, the observation time cannot be longer than a few lifetimes. $\Delta t$ is thus of the order of $\tau$ in the rest frame of the particle. As a consequence, the intrinsic uncertainty of the particle energy cannot be smaller than:
$$
\Delta E \geq(2 \tau)^{-1}
$$

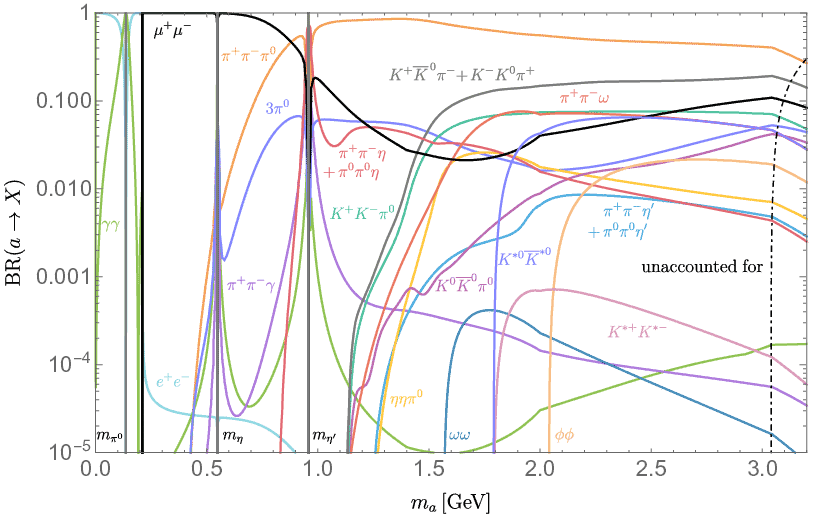
核物理代考

物理代写|核物理代考NUCLEAR PHYSICS代写|LIFETIMES AND BRANCHING RATIOS

在 eqn 2.90 中，洛伦兹变换后唯一变化的项是 $E_a$ 衰减率转换为:
$$
\Gamma_{i \rightarrow f}^{\prime}=\Gamma_{i \rightarrow f} / \gamma
$$
例如，实验室框架中的观察者看到的 $\mu$ 子衰变比 $\mathrm{CM}$ 慢。由于 $\mu$ 子总是在 $e^{-} \nu_\mu \bar{\nu}_e$, 它的寿命很简单 $\Gamma^{-1}$. 这是量子力学的结果：对于一个系统 $N$ 处 于同一不稳定状态的粒子，达到基态的粒子数 $d t$ 是 $d N=-N \Gamma d t$. 负号表示不稳定粒子的数量随时间减少而处于基态的粒子数量增加。一段时间 后存活下来的不稳定粒子 $t$ 然后是:
$$
N(t)=N(0) e^{-\Gamma t} .
$$

物理代写|核物理代考NUCLEAR PHYSICS代 写|UNSTABLE STATES

即使非相对论量子力学无法描述粒子的产生和湮石 Bromberg, 1976，它配备了描述不稳定状态的形式主义。在空间中找到不稳定粒子的概率随时 间降低，波函数逐渐消失为:
$$
|\psi(\mathbf{x}, t)|^2=|\psi(\mathbf{x}, 0)|^2 e^{-t / \tau}
$$
阻尼项是与方程 2.95 的衰减定律兼容的指数函数。辠定谔方程的定态不再存在:
$$
\psi(\mathbf{x}, t)=\psi(\mathbf{x}) e^{-i E t}
$$
但被消失的状态所取代 $t \rightarrow+\infty:$
$$
\psi(\mathbf{x}, t)=\psi(\mathbf{x}) e^{-i E t} e^{-t / 2 \tau}
$$
消失状态不是静止状态，它的大量消失会带来微妙的 QM 效应。由于海森堡第二节的不确定性原理。B.4，可以任意精度测量静止状态的能量，前 提是 $\Delta E \Delta t \geq \hbar / 2$ 或者 $i n N U \Delta E \geq 1 /(2 \Delta t)$. 如果粒子经不起时间的流逝，那么观测时间就不可能超过几个生命周期。 $\Delta t$ 因此是 $\tau$ 在粒子的静 止坐标系中。因此，粒子能量的固有不确定性不能小于:
$$
\Delta E \geq(2 \tau)^{-1}
$$

物理代写|核物理代考Nuclear Physics代写 请认准exambang™. exambang™为您的留学生涯保驾护航。

微观经济学代写

微观经济学是主流经济学的一个分支，研究个人和企业在做出有关稀缺资源分配的决策时的行为以及这些个人和企业之间的相互作用。my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学Mathematics代写服务。我们的专家在图论代写Graph Theory代写方面经验极为丰富，各种图论代写Graph Theory相关的作业也就用不着 说。

线性代数代写

线性代数是数学的一个分支，涉及线性方程，如：线性图，如：以及它们在向量空间和通过矩阵的表示。线性代数是几乎所有数学领域的核心。

博弈论代写

现代博弈论始于约翰-冯-诺伊曼（John von Neumann）提出的两人零和博弈中的混合策略均衡的观点及其证明。冯-诺依曼的原始证明使用了关于连续映射到紧凑凸集的布劳威尔定点定理，这成为博弈论和数学经济学的标准方法。在他的论文之后，1944年，他与奥斯卡-莫根斯特恩（Oskar Morgenstern）共同撰写了《游戏和经济行为理论》一书，该书考虑了几个参与者的合作游戏。这本书的第二版提供了预期效用的公理理论，使数理统计学家和经济学家能够处理不确定性下的决策。

微积分代写

微积分，最初被称为无穷小微积分或 “无穷小的微积分”，是对连续变化的数学研究，就像几何学是对形状的研究，而代数是对算术运算的概括研究一样。

它有两个主要分支，微分和积分；微分涉及瞬时变化率和曲线的斜率，而积分涉及数量的累积，以及曲线下或曲线之间的面积。这两个分支通过微积分的基本定理相互联系，它们利用了无限序列和无限级数收敛到一个明确定义的极限的基本概念 。

计量经济学代写

什么是计量经济学？
计量经济学是统计学和数学模型的定量应用，使用数据来发展理论或测试经济学中的现有假设，并根据历史数据预测未来趋势。它对现实世界的数据进行统计试验，然后将结果与被测试的理论进行比较和对比。

根据你是对测试现有理论感兴趣，还是对利用现有数据在这些观察的基础上提出新的假设感兴趣，计量经济学可以细分为两大类：理论和应用。那些经常从事这种实践的人通常被称为计量经济学家。

Matlab代写

MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中，其中问题和解决方案以熟悉的数学符号表示。典型用途包括：数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发，包括图形用户界面构建MATLAB 是一个交互式系统，其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题，尤其是那些具有矩阵和向量公式的问题，而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问，这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展，得到了许多用户的投入。在大学环境中，它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域，MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要，工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数（M 文件）的综合集合，可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。