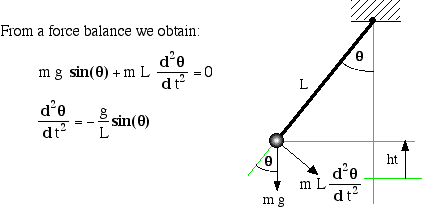MY-ASSIGNMENTEXPERT™可以为您提供coursicle.com Math220 Ordinary Differential Equations常微分方程的代写代考和辅导服务!

Math220课程简介
Grading policy: The grade will be based on the weekly homework (25%), on the in-class midterm exam (30%) and on the in-class (i.e. not take-home, to take place during finals week, as designated by the registrar) final exam (45%).
The homework will be due in class or in the instructor’s mailbox by 9am on the designated day, which will usually (but not always) be Fridays. You are allowed to discuss the homework with others in the class, but you must write up your homework solution by yourself. Thus, you should understand the solution, and be able to reproduce it yourself. This ensures that, apart from satisfying a requirement for this class, you can solve the similar problems that are likely to arise on the exams.
Prerequisites
Course Description : We will cover most of the textbook. This includes formulating physical systems as differential equations, learning various methods to solve them, basics of infinite series and how to use them to solve differential equations, studying linear and nonlinear systems of differential equations, and topological methods.
Learning Outcomes:: The broad learning goals of the course are:
Model various physical phenomena with differential equations
Understand that solutions to differential equations can be addressed with both exact methods and qualitative methods
Math220 Ordinary Differential Equations HELP(EXAM HELP, ONLINE TUTOR)
Problem 1. Classify the following PDEs by degree of non-linearity (linear, semilinear, quasilinear, fully nonlinear):
(1) $(\cos x) u_x+u_y=u^2$.
(2) $u u_{t t}=u_{x x}$.
(3) $u_x-e^x u_y=\cos x$.
(4) $u_{t t}-u_{x x}+e^u u_x=0$.
Solution. They are: (1) semilinear, (2) quasilinear, (3) linear, (4) semilinear.
Problem 2.
(1) Solve
$$
u_x+(\sin x) u_y=y, u(0, y)=0 .
$$
(2) Sketch the projected characteristic curves for this PDE.
Solution. The characteristic ODEs are
$$
\frac{d x}{d s}=1, \frac{d y}{d s}=\sin x, \frac{d z}{d s}=y
$$
We first solve the $x$ ODE, substitute the solution into the $y$ ODE, and then substitute the solution into the $z$ ODE. So:
$$
\begin{aligned}
& x(r, s)=s+c_1(r) \
& \frac{d y}{d s}=\sin \left(s+c_1(r)\right) \Rightarrow y(r, s)=-\cos \left(s+c_1(r)\right)+c_2(r) \
& \frac{d z}{d s}=-\cos \left(s+c_1(r)\right)+c_2(r) \Rightarrow z(r, s)=-\sin \left(s+c_1(r)\right)+c_2(r) s+c_3(r) .
\end{aligned}
$$
The initial condition is that the characteristic curves go through
$$
{(0, r, 0): r \text { arbitrary }}
$$
at $s=0$, i.e. that
$$
(0, r, 0)=\left(c_1(r),-\cos \left(c_1(r)\right)+c_2(r),-\sin \left(c_1(r)\right)+c_3(r)\right) .
$$
Thus, $c_1(r)=0,-1+c_2(r)=r$. i.e. $c_2(r)=r+1$, and $c_3(r)=0$, so the solution of the characteristic ODEs satisfying the initial conditions is
$$
(x, y, z)=(s,-\cos s+r+1,-\sin s+(r+1) s) .
$$
We need to invert the $\operatorname{map}(r, s) \mapsto(x(r, s), y(r, s))$, i.e. express $(r, s)$ in terms of $(x, y)$. This gives $s=x$, and $r=y+\cos s-1=y+\cos x-1$. The solution of the $\mathrm{PDE}$ is thus
$$
u(x, y)=z(r(x, y), s(x, y))=-\sin x+(y+\cos x) x
$$
The projected characteristic curves are the curves along which $r$ is constant, i.e. they are $y=-\cos x+C, C$ a constant (namely $r+1$ ).

MY-ASSIGNMENTEXPERT™可以为您提供UNIVERSITY OF ILLINOIS URBANA-CHAMPAIGN MATH2940 linear algebra线性代数课程的代写代考和辅导服务! 请认准MY-ASSIGNMENTEXPERT™. MY-ASSIGNMENTEXPERT™为您的留学生涯保驾护航。