MY-ASSIGNMENTEXPERT™可以为您提供 uq.edu.au MATH3202 Operations Research运筹学的代写代考和辅导服务!
MATH3202课程简介
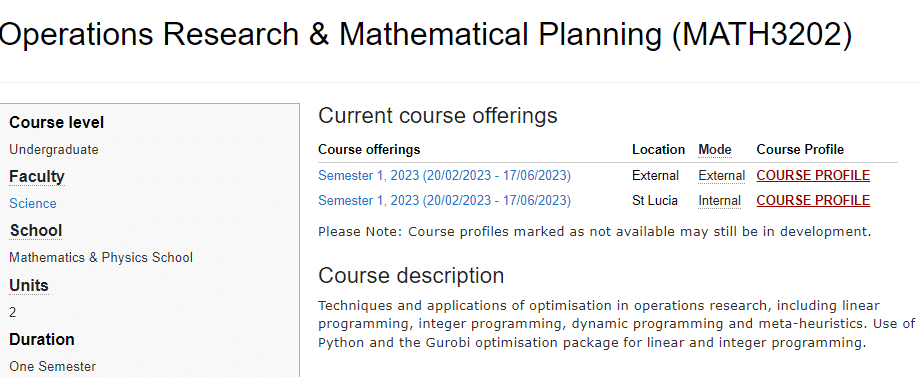
Course description
Techniques and applications of optimisation in operations research, including linear programming, integer programming, dynamic programming and meta-heuristics. Use of Python and the Gurobi optimisation package for linear and integer programmi
Operations research is the mathematical science of decision making. It provides ways to find the best outcomes subject to the constraints of limited resources. This course covers key mathematical and computational techniques in the area. It develops skills in modelling and solving real problems, using appropriate software, and report writing.
Prerequisites
Topics discussed include linear programming, integer programming, dynamic programming and metaheuristics.
Course Changes in Response to Previous Student Feedback
The course will again use Python as a common tool across all sections of the course. Based on student feedback, additional support for starting with Python will be provided.
MATH3202 Operations Research HELP(EXAM HELP, ONLINE TUTOR)
The postal department is considering the purchase of vehicles to pick up and deliver mail from various offices. They are considering three types of vehicles. The cost of each of these are ₹ 5 lakhs, ₹ 10 lakhs and ₹ 8 lakhs per vehicle, respectively. These require a crew of 2,4 and 4 persons per day considering multiple shifts. They expect these to run for 60,100 and $80 \mathrm{~km}$ per day. They expect that the total distance to be covered by the vehicles per day would be $2000 \mathrm{~km}$. Based on the fuel economy, the operating cost per day for these vehicles are $₹ 200$, ₹ 350 and ₹ 300 per day. They have a budget restriction of ₹ 1.6 crore and have 80 people available as crew. Formulate a model to minimize the operating costs.
Solution: Let us define
$X_1=$ Number of vehicles of Type $A$ being purchased
$X_2=$ Number of vehicles of Type $B$ being purchased
$X_3=$ Number of vehicles of Type $C$ being purchased
Objective function: Minimize $Z=200 X_1+350 X_2+300 X_3$
Constraints:
$$
\begin{aligned}
5 X_1+10 X_2+8 X_3 & \leq 160 \text { (Budget constraint) } \
2 X_1+4 X_2+4 X_3 & \leq 80 \text { (Crew constraint) } \
60 X_1+100 X_2+80 X_3 & \geq 2000 \
X_1, X_2, X_3 & \geq 0, \text { and integers }
\end{aligned}
$$
We can leave the integer restriction since we are formulating an LP problem.
A Media planning company has to optimally allocate its client’s advertising budget using linear programming. The eight possible advertising vehicles are television (national and private channels), newspapers (one English, one Hindi and one in Bengali), local magazine and on its website and on a popular radio channel. The client is also interested in targeting two different types of audience for their products (working women and retired couples). The company estimates that for every rupee spent on vehicle $\boldsymbol{i}$, the number of people exposed in category $\boldsymbol{j}$ is $a_{i j}$.
Consider the following additional requirements:
- There is a budget restriction of $₹ B$.
- The client wants a minimum of $d_j$ people of type $j$ to be exposed to the advertisements.
- There is an upper limit of $₹ C$ that can be spent on television advertisements.
- At least $R$ people should be exposed through radio channel.
(a) Formulate a linear programming problem for the above situation.
(b) Will the client end up spending on all the eight possible advertising vehicles?
Solution: Let the money spent on vehicle $i$ be $X_i$. The objective function is to maximize total exposure.
$$
\text { Maximize } \sum_{i=1}^8 \sum_{j=1}^2 a_{i j} X_j
$$
The constraints are:
(Budget restriction)
(Required exposure of each type)
(Limit on television advertisement)
$$
\begin{aligned}
a_{81} X_1+a_{82} X_2 & \geq R \
X_j & \geq 0
\end{aligned}
$$

MY-ASSIGNMENTEXPERT™可以为您提供UNIVERSITY OF ILLINOIS URBANA-CHAMPAIGN MATH2940 linear algebra线性代数课程的代写代考和辅导服务! 请认准MY-ASSIGNMENTEXPERT™. MY-ASSIGNMENTEXPERT™为您的留学生涯保驾护航。

