数学代写|Math56a Stochastic processes

MY-ASSIGNMENTEXPERT™可以为您提供brandeis Math56a Stochastic processes随机过程课程的代写代考和辅导服务！

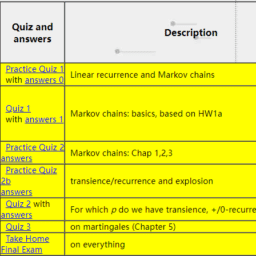
Math56a课程简介

In a continuous time Markov chain, transition events can occur at any time with a certain probability density. The corresponding deterministic model is a first order differential equation. This includes the “general stochastic epidemic.”

The number of states in a Markov chain is either finite or countably infinite. When the collection of states becomes a continuum, e.g., the price of a stock option, we no longer have a “Markov chain.” We have a more general stochastic process. Under very general conditions we obtain a Wiener process, also known as Brownian motion. The mathematics of hedging implies that stock options should be priced as if they are exactly given by this process. Ito’s formula explains how to calculate (or try to calculate) stochastic integrals which give the long term expected values for a Wiener process.

Prerequisites 

A stochastic process is a random process which evolves with time. The basic model is the Markov chain. This is a set of “states” together with transition probabilities from one state to another. For example, in simple epidemic models there are only two states: $S=$ “susceptible” and $I=$ “infected.” The probability of going from $S$ to $I$ increases with the size of $I$. In the simplest model The $S \rightarrow I$ probability is proportional to $I$, the $I \rightarrow S$ probability is constant and time is discrete (for example, events happen only once per day). In the corresponding deterministic model we would have a “difference equation.”

Math56a Stochastic processes HELP（EXAM HELP， ONLINE TUTOR）

(a) To find the unique invariant distribution $\pi$, we need to solve the equation $\pi P = \pi$. This leads to the following system of equations: \begin{align*} \pi_1 &= 0.4\pi_3 + 0.7\pi_4 \ \pi_2 &= 0.4\pi_3 \ \pi_3 &= 0.2\pi_1 \ \pi_4 &= 0.3\pi_3 + \pi_2. \end{align*} Solving this system of equations, we get $\pi_1 = \frac{14}{47}$, $\pi_2 = \frac{4}{47}$, $\pi_3 = \frac{28}{235}$, and $\pi_4 = \frac{75}{235}$. To see that this is the unique invariant distribution, note that the matrix $P$ is irreducible (since there is a path from any state to any other state) and aperiodic (since there is a self-loop in state 1). Therefore, by the Perron-Frobenius theorem, there exists a unique invariant distribution, and it is positive (since $P$ is non-negative and irreducible).

(b) The communication classes are ${1}$, ${2,3}$, and ${4}$. This can be seen by noting that there is no path from state 1 to states 2 or 3, but there is a path from state 2 to state 3 (and vice versa), and there is no path from state 1 to state 4 (or vice versa).

(c) Since state 1 is transient, the probability that $X_{100}$ is in the transient class given that you start in the transient class is 1. If you start at a random location, the probability that $X_{100}$ is in the transient class is the sum of the probabilities of being in each transient state at time 100, weighted by the initial probabilities of being in each state. Since state 1 has initial probability 1, we have: \begin{align*} &\text{Pr}(X_{100} \text{ is in transient class }| X_0 \text{ is random}) \ &\qquad= \text{Pr}(X_{100}=2|X_0=1)\text{Pr}(X_0=1) + \text{Pr}(X_{100}=3|X_0=1)\text{Pr}(X_0=1) + \text{Pr}(X_{100}=2|X_0=3)\text{Pr}(X_0=3) + \text{Pr}(X_{100}=3|X_0=2)\text{Pr}(X_0=2) \ &\qquad= 0 + 0 + \left(\frac{14}{47}\right)^2(0.4^{100}) + \left(\frac{4}{47}\right)^2(0.4^{100}) \ &\qquad\approx 0.000005. \end{align*} The approximation assumes that the probability of being in state 2 or 3 at time 100 is effectively 0, which is reasonable given that $0.4^{100}$ is an extremely small number.

MY-ASSIGNMENTEXPERT™可以为您提供UNIVERSITY OF ILLINOIS URBANA-CHAMPAIGN MATH2940 linear algebra线性代数课程的代写代考和辅导服务！ 请认准MY-ASSIGNMENTEXPERT™. MY-ASSIGNMENTEXPERT™为您的留学生涯保驾护航。