MY-ASSIGNMENTEXPERT™可以为您提供 mtlc.ua.edu Math113 Complex Analysis复分析的代写代考和辅导服务!
这是阿拉巴马大学复分析课程的代写成功案例。
Math113课程简介
Hey there Math 113 student!
We have designed this course on Analysis I: Complex Function Theory for those who are studying at Harvard University and want to consolidate their understanding and learn from experts and professors, at any time, and from anywhere.
This personalized course is stocked with video tutorials, practice questions, study guides, and 3 personalized tutor responses to ensure that you fully understand the material in all the subjects.
We aim to provide you with the materials so that you can learn independently, at your own pace, and in your own time. You can rewatch the videos as many times as you need before moving on, so there is no fear of falling behind or not reaching any deadlines.
As this is a customised course, you can be sure that all the material is relevant, and you aren’t going to waste time learning something that you won’t be tested on!
Once you have watched the videos, practice what you have learned with our downloadable workbooks to test your knowledge and maximize your learning.
Happy studying, and we are here to help if you have any questions!
Prerequisites
COURSE DESCRIPTION
This course is a continuation of Math 112. It includes the study of trigonometric and inverse trigonometric functions, as well as extensive work with trigonometric identities and equations. Other topics contained in this course are: polar coordinates, complex numbers, DeMoivre’s Theorems, vectors, and conic sections.
The course presents the essential characteristics and basic processes of inquiry and analysis in the discipline.
The course encourages the development of critical thinking skills and requires students to analyze, synthesize, and evaluate
knowledge.
The course considers its subjects in relation to other disciplines and to the human condition.
The course is not limited to majors in any discipline.
The course does not focus on professional skills.
LEARNING OUTCOMES FOR THIS COURSE
Math113 Complex Analysis HELP(EXAM HELP, ONLINE TUTOR)
Odd-even integers
i) Prove that the sum of two odd integers is an even integer.
ii) Prove that the product of two integers is odd if and only if the two integers are both odd.
iii) Suppose that the product of two integers is odd. Prove that the sum of those two integers is even.
iv) Suppose that the sum of the squares of two integers is odd. Prove that one of the two integers is even and the other is odd.
v) Prove that the product of two consecutive integers is even. Prove that the product of three consecutive integers is an integer multiple of 6 .
vi) Prove that the sum of two consecutive integers is odd. Prove that the sum of three consecutive integers is an integer multiple of 3 .
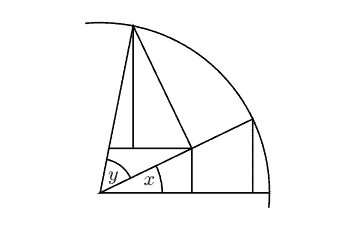
1.1.16. (Cf. Exercise 10.2.3.) Draw a unit circle and a line segment from the center to the circle. Any real number $x$ uniquely determines a point $P$ on the circle at angle $x$ radians from the line. Draw the line from that point that is perpendicular to the first line. The length of this perpendicular line is called $\sin (x)$, and the distance from the intersection of the two perpendicular lines to the center of the circle is called $\cos (x)$. This is our definition of $\cos$ and $\sin$.
Consider the following picture inside the circle of radius 1 :
i) Label the line segments of lengths $\sin (x), \sin (y), \cos (y)$.
ii) Use ratio geometry (from page 20) to assert that the smallest vertical line in the bottom triangle has length $\sin (x) \cos (y)$.
iii) Use trigonometry and ratio geometry to assert that the vertical line in the top triangle has length $\sin (y) \cos (x)$.
iv) Prove that $\sin (x+y)=\sin (x) \cos (y)+\sin (y) \cos (x)$.
Determine the truth value of each statement. Justify your answer.
i) For all real numbers $a, b,(a+b)^2=a^2+b^2$.
ii) For all real numbers $a, b,(a+b)^2=a^2+2 a b+b^2$.
iii) For all real numbers $x<5, x^2>16$.
iv) There exists a real number $x<5$ such that $x^2<25$. v) There exists a real number $x$ such that $x^2=-4$. vi) There exists a real number $x$ such that $x^3=-8$. vii) For every real number $x$ there exists a positive integer $n$ such that $x^n>0$.
viii) For every real number $x$ and every integer $n,|x|<x^n$.
ix) For every integer $m$ there exists an integer $n$ such that $m+n$ is even.
x) There exists an integer $m$ such that for all integers $n, m+n$ is even.
xi) For every integer $n, n^2-n$ is even.
xii) Every list of 5 consecutive integers has one element that is a multiple of 5 .
xiii) Every odd number is a multiple of 3 .
Determine and justify the truth value of the following statements.
i) 3 is odd or 5 is even.
ii) If $n$ is even, then $3 n$ is prime.
iii) If $3 n$ is even, then $n$ is prime.
iv) If $n$ is prime, then $3 n$ is odd.
v) If $3 n$ is prime, then $n$ is odd.
vi) $(P$ and $Q) \Rightarrow P$.
Sometimes statements are not written precisely enough. For example, “It is not the case that 3 is prime and 5 is even” may be saying “not (3 is prime and 5 is even),” or it may be saying “( not (3 is prime)) and (5 is even).” The first option is true and the second is false.
Similarly analyze several possible interpretations of the following ambiguous sentences:
i) If 6 is prime then 7 is even or 5 is odd.
ii) It is not the case that 3 is prime or if 6 is prime then 7 is even or 5 is odd.

MY-ASSIGNMENTEXPERT™可以为您提供 MTLC.UA.EDU MATH113 COMPLEX ANALYSIS复分析的代写代考和辅导服务!