MY-ASSIGNMENTEXPERT™可以为您提供users.cse.Math8211 Commutative Algebra交换代数课程的代写代考和辅导服务!
这是明尼苏达大学 交换代数课程的代写成功案例。
Math8211课程简介
TEXT: Commutative algebra. With a view toward algebraic geometry by David Eisenbud, 1995.
Prerequisite: Math 8201-02 General Algebra or some previous experience with groups, rings, and fields.
DESCRIPTION: Commutative algebra stands at the crossroads of algebra, number theory, and algebraic geometry. It is subsumed by algebraic geometry as the local study of algebraic varieties, somewhat similar to analysis in R^n succumbing to the theory of manifolds. Homological algebra is a powerful algebraic tool used in many fields of mathematics, including commutative and noncommutative algebra, group theory, Lie theory, several complex variables, geometry and topology, PDE, combinatorics, functional analysis, numerical analysis, and mathematical physics, to name a few.
Prerequisites
CONTENT: In the Fall Semester, we will study commutative algebra. This will include commutative rings and modules over them, Noetherian rings, Krull dimension theory, Noether normalization, the so-called Nullstellensatz, the spectrum of a ring, rings of fractions and localization, primary decomposition, discrete valuation rings, normal integral domains, and regular local rings. The geometric view of a commutative ring as the ring of functions on a space will be emphasized.
The homological algebra part of the course will be taught in the Spring Term by Bernard Badzioch. The topics will include complexes, homology, resolutions and derived functors. These notions will be put into the context of two different axiomatic approaches to homological algebra: via triangulated categories and via closed model categories. Additional topics will include Koszul complex, Hochschild homology and cyclic homology. Applications to commutative algebra such as the notion of depth and Cohen-Macaulay rings, algebraic geometry and topology will be discussed.
Math8211 Commutative Algebra HELP(EXAM HELP, ONLINE TUTOR)
Part of 2.4 of Eisenbud) Let $k$ be a field and let $m, n$ be integers. Describe as explicitly as possible the following. For example, if the object is a finite-dimensional vector space, what is its dimension?
a. $\operatorname{Hom}{k[x]}\left(k[x] /\left(x^n\right), k[x] /\left(x^m\right)\right)$ b. $k[x] /\left(x^n\right), \otimes{k[x]} k[x] /\left(x^m\right)$
c. $k[x] \otimes_k k[x]$ (describe this as an algebra.
Eisenbud question 2.11 It is very similar for modules to something we did for rings.
Let $U \subset R$ be a multiplicative subset not containing any zero divisors of a commutative ring $R$. We can regard $R$ as the set of elements $\frac{r}{1}$ of $R\left[U^{-1}\right]$ where $r$ ranges through $R$. If $S$ is a ring with $R \subseteq S \subseteq R\left[U^{-1}\right]$, show that $S\left[U^{-1}\right]=R\left[U^{-1}\right]$.
Suppose that $U$ and $V$ are two multiplicative subsets of the commutative ring $R$ with $U \subseteq V$. Writing $V^{\prime}$ for the image of $V$ in $R\left[U^{-1}\right]$, show that $R\left[U^{-1}\right]\left[V^{\prime-1}\right]=R\left[V^{-1}\right]$.
Problem 1. For a ring $A$, prove that $A^m$ and $A^n$ are isomorphic as $A$-modules, if and only if $m=n$. Hint: use the existence of maximal ideals.
Problem 2. If $A$ is a ring and $I$ a finitely generated ideal which is idempotent, i.e., satisfies $I=I^2$, prove that $I$ is generated by a single idempotent element. Hint: use a corollary from the determinant trick we used to prove Nakayama’s lemma.
Problem 3. Let $A$ be an Artinian integral domain i.e., one whose ideals satisfy the descending chain condition. Prove that $A$ is a field. Deduce that every prime ideal of an Artinian ring is maximal.
Problem 4. Prove the Hilbert basis theorem for the formal power series ring $A[[X]]$ for Noetherian $A$.
(1) If $a$ is a unit and $x$ is nilpotent, prove that $a+x$ is again a unit.
(2) Let $A$ be a ring, and $I \subset \operatorname{nilrad} A$ an ideal; if $x \in A$ maps to an invertible element of $A / I$, prove that $x$ is invertible in $A$.
Problem 6. Show that if $A$ is a reduced ring and has finitely many minimal prime ideals $P_i$, i.e., minimal elements in the set of prime ideals of $A$, then $A \hookrightarrow$ $\bigoplus_{i=1}^n A / P_i$; moreover the image has nonzero intersection with each summand.
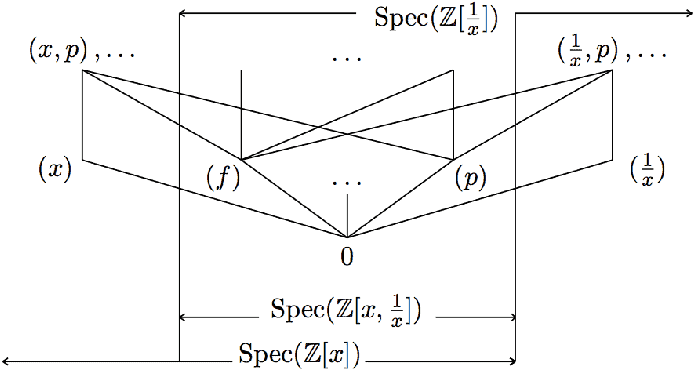
Problem 7. Describe Spec $\mathbb{R}[X]$ in terms of $\mathbb{C}$.
Problem 8. Let $A$ be a ring with zerodivisors, i.e., not an integral domain. Prove that $A$ has either nonzero nilpotent elements, or more than one minimal prime ideal.

MY-ASSIGNMENTEXPERT™可以为您提供UNIVERSITY OF ILLINOIS URBANA-CHAMPAIGN MATH2940 linear algebra线性代数课程的代写代考和辅导服务! 请认准MY-ASSIGNMENTEXPERT™. MY-ASSIGNMENTEXPERT™为您的留学生涯保驾护航。