如果你也在 怎样代写离散数学Discrete Mathematics MA210这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。离散数学Discrete Mathematics是数学的一个分支,研究一般代数环境中的同源性。它是一门相对年轻的学科,其起源可以追溯到19世纪末的组合拓扑学(代数拓扑学的前身)和抽象代数(模块和共轭理论)的研究,主要是由亨利-庞加莱和大卫-希尔伯特提出。
离散数学Discrete Mathematics是研究同源漏斗和它们所带来的复杂的代数结构;它的发展与范畴理论的出现紧密地联系在一起。一个核心概念是链复合体,可以通过其同调和同调来研究。它在代数拓扑学中发挥了巨大的作用。它的影响逐渐扩大,目前包括换元代数、代数几何、代数理论、表示理论、数学物理学、算子矩阵、复分析和偏微分方程理论。K理论是一门独立的学科,它借鉴了同调代数的方法,正如阿兰-康尼斯的非交换几何一样。
离散数学Discrete Mathematics代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。 最高质量的离散数学Discrete Mathematics作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此离散数学Discrete Mathematics作业代写的价格不固定。通常在专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
同学们在留学期间,都对各式各样的作业考试很是头疼,如果你无从下手,不如考虑my-assignmentexpert™!
my-assignmentexpert™提供最专业的一站式服务:Essay代写,Dissertation代写,Assignment代写,Paper代写,Proposal代写,Proposal代写,Literature Review代写,Online Course,Exam代考等等。my-assignmentexpert™专注为留学生提供Essay代写服务,拥有各个专业的博硕教师团队帮您代写,免费修改及辅导,保证成果完成的效率和质量。同时有多家检测平台帐号,包括Turnitin高级账户,检测论文不会留痕,写好后检测修改,放心可靠,经得起任何考验!
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
我们在数学Mathematics代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学Mathematics代写服务。我们的专家在离散数学Discrete Mathematics代写方面经验极为丰富,各种离散数学Discrete Mathematics相关的作业也就用不着 说。
数学代写|离散数学代写Discrete Mathematics代考|Private-Key Cryptography
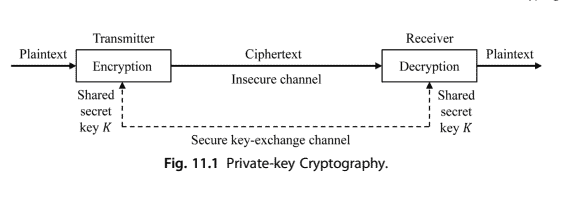
Private-key cryptography is based on sharing secrecy by permuting or substituting characters in the plaintext. All classical ciphers with no exception fall into private-key cryptography. The private-key cryptography is often used for long messages, for they require less time to encrypt. In private-key cryptography, an $n$-bit block of plaintext is encrypted and an $n$-bit block of ciphertext is decrypted. If a message block has fewer than $n$ bits, padding must be added to make it an $n$-bit block. The common values of $n$ are 64 , 128, 256, and 512 bits. Private-key cryptography uses the same $k$-bit key for both the encryption at the transmitter and the decryption at the receiver, as shown in Fig. 11.1.
In private-key cryptography, once the key is known, both encryption and decryption can be carried out.
In private-key cryptography, the decryption algorithm is the inverse of the encryption algorithm, and the number of private keys for $N$ users to communicate is $\frac{N(N-1)}{2}$, as each pair must have a unique private key. The number of keys grows quadratically, thus making these systems infeasible for larger-scale use. In private-key distribution, a trusted third party, referred to as a key distribution center (KDC), is used. In privatekey cryptography, each user establishes a shared secret key with KDC. The secret keys, created by $\mathrm{KDC}$, are used exclusively between $\mathrm{KDC}$ and the users and not among the users themselves. When a user wants to transmit secretly with another one, the transmitter then asks KDC for a session (temporary) secret key to be used between the two users. A session private key between two parties is used only once.
A widely known example of private-key cryptography is the Data Encryption Standard (DES), which has a block cipher structure. DES was developed in the 1970 s, and for over 25 years, DES was used by the US government to protect binary data during transmission and storage in computer systems and by the banking industry and businesses to protect financial transactions for commercial data security. At the transmitter, a 64-bit plaintext is created into a 64-bit ciphertext, and at the receiver, a 64-bit cipher text is converted back to a 64-bit plaintext, noting that in DES, the same 56-bit key is used for both encryption and decryption. The key in fact consists of 64 bits. However, only 56 of these are actually used by the algorithm. Eight bits are used solely for error detection and are thereafter discarded. Despite its deprecation as an official standard, DES remains popular; it is used across a wide range of applications, including ATM encryption, email privacy, and secure remote access.
数学代写|离散数学代写Discrete Mathematics代考|Public-Key Cryptography
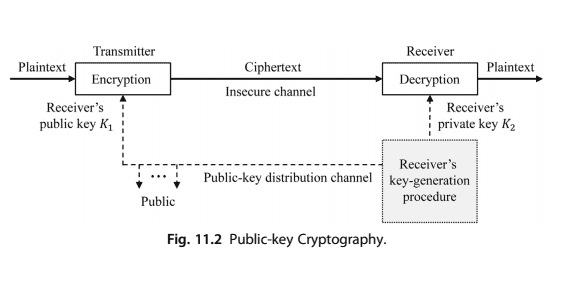
Public-key cryptography is based on personal secrecy rather than sharing secrecy. In public-key cryptography, the plaintext and ciphertext are numbers that are manipulated by mathematical functions. In public-key cryptography, a public key and a private key are used (see Fig. 11.2). It is a salient requirement that it must not be possible to determine the private key from the public key. In general, the public key is small, and the private key is large. A pair of keys can be used many times. The number of keys for $N$ users to communicate is $2 \mathrm{~N}$. The algorithm is complex and more efficient for short messages.
In public-key distribution, an organization, known as a certification authority (CA), is used. In public-key cryptography, public keys, like secret keys, need to be distributed securely; otherwise, the process can be subject to forgery. CA first checks the identification of a user, asks the user’s public key, and writes it on the certificate. To prevent the certificate itself from being forged, CA signs the certificate with its own private key, which is difficult to be forged. The user uploads the signed certificate. Anyone who wants a user’s public key downloads the user’s signed certificate and then uses the CA’s public key to obtain the user’s public key.
Message authentication protects two communicating parties from any third party; it does not, however, protect the two parties against each other. In situations where something more than authentication is needed, the digital signature is the most attractive solution; in addition, it can also prevent denial and forgery. Public-key cryptography can be used to provide nonrepudiation by producing a digital signature. A digital signature uses a pair of private-public keys belonging to the sender to provide message integrity and message authentication. In short, a digital signature is reminiscent of an ordinary signature, as they both have the benefit of being easy to produce but difficult enough for anyone else to forge. A digital signature can be permanently tied to the content of the message being signed, and it cannot be moved then from one digital file to another, for any attempt will be detected.
In a digital signature system, on the one hand, the messages are normally long, but on the other hand, we must use public-key cryptography systems that are very inefficient when dealing with long messages. The solution is to create a digest of a message through a hashing function, for instance, a checksum is produced that is much smaller than the message. Therefore the transmitter first produces a digest, then encrypts it using its own private key to produce the signature, and then sends the signature along with the message to the receiver. At the receiver, the signer’s public key is applied to the signature to get the transmitted digest, and the digest is also directly determined from the message. If both digests are the same, then only the given transmitter could have issued the message and that the message has maintained its integrity.
It is important to highlight the distinction between how private and public keys are used in digital signature, vis-à-vis in cryptography for confidentiality. In digital signature, the signer (transmitter) signs the message digest with the signer’s private key and the verifier (receiver) verifies with the signer’s public key. In contrast, in cryptography, the public and private keys of the receiver are used in the process.
Another important application of public-key cryptography is the digital envelope. A digital envelope is a framework for data encryption, in which the data is encrypted under a secret key using a private-key cryptography, such as DES or AES, while this secret key is encrypted using a public-key cryptography such as RSA, and sent to the other party. In short, a public key cryptography can be used to distribute private keys to pairs of individuals wishing to communicate.
离散数学代写
数学代写|离散数学代写DISCRETE MATHEMATICS代考|PRIVATE-KEY CRYPTOGRAPHY
私钥密码学基于通过置换或替换明文中的字符来共享机密性。所有经典密码都无一例外地属于私钥密码学。私钥加密通常用于长消息,因为它们 需要更少的时间来加密。在私钥密码学中,一个 $n$-bit 明文块被加密并且 $n$ 位密文块被解密。如果消息块少于 $n$ 位,必须添加填充以使其成为 $n$-位 块。的共同价值观 $n$ 分别为 $64 、 128 、 256$ 和 512 位。私钥密码术使用相同的 $k$ 位密钥,用于发送端的加密和接收端的解密,如图 11.1 所示。
在私钥密码学中,一旦知道密钥,就可以进行加密和解密。
在私钥密码学中,解密算法是加密算法的逆算法,私钥的数量为 $N$ 用户交流是 $\frac{N(N-1)}{2}$ ,因为每一对都必须有一个唯一的私钥。密钥的数量呈二次 方增长,从而使这些系统无法大规模使用。在私钥分发中,受信任的第三方,称为密钥分发中心 $K D C$ ,用来。在私钥密码学中,每个用户与 $K D C$ 建立一个共享密钥。秘密密钥,由KDC, 专门用于KDC和用户,而不是用户本身。当一个用户想与另一个用户秘密传输时,发送器然后向 KDC 请求会话temporary两个用户之间使用的密钥。双方之间的会话私钥仅使用一次。
私钥加密的一个广为人知的例子是数据加密标准 $D E S \mathrm{~ , 它 具 有 分 组 密 码 结 构 。 D E S ~ 是 在 ~} 1970$ 年代开发的,25多年来,DES被美国政府用于保护 计算机系统中传输和存储过程中的二进制数据,以及被银行业和企业用于保护金融交易的商业数据安全。在发送方,将 64 位明文创建为 64 位密 文,在接收方,将 64 位密文转换回 64 位明文,注意在 DES 中,相同的 56 位密钥用于加密和解密。密钥实际上由 64 位组成。然而,算法实际上只 使用了其中的 56 个。八位仅用于错误检测,然后被丟弃。尽管作为官方标准已被弃用,DES 仍然很受欢迎;它用于广泛的应用程序,
数学代写|离散数学代写DISCRETE MATHEMATICS代考|PUBLIC-KEY CRYPTOGRAPHY
公钥加密基于个人保密而非共享保密。在公钥密码学中,明文和密文是由数学函数处理的数字。在公钥密码学中,使用公钥和私钥seeFig. 11.2. 一个突出的要求是不能从公钥中确定私钥。一般来说,公钥小,私钥大。一对钥匙可以多次使用。键的数量 $N$ 用户交流是 $2 \mathrm{~N}$. 该算法复杂,对于 短消息更有效。
在公钥分发中,一个称为证书颁发机构的组织 $C A$ ,用来。在公钥密码学中,公钥和私钥一样,需要安全地分发;否则,该过程可能会被仂造。 CA首先检查用户的身份,询问用户的公钥,并将其写在证书上。为了防止证书本身被偶造,CA使用自己的私钥对证书进行签名,很难被伪造。用 户上传签名证书。任何想要用户公钥的人都可以下载用户的签名证书,然后使用 CA 的公钥来获取用户的公钥。
消息认证保护两个通信方免受任何第三方的侵害;然而,它并没有保护两方相互对抗。在需要的不仅仅是身份验证的情况下,数字签名是最有吸 引力的解决方案;此外,它还可以防止否认和伪造。公钥加密可用于通过生成数字签名来提供不可否认性。数字签名使用属于发送方的一对私钥公钥来提供消息完整性和消息身份验证。简而言之,数字签名让人联想到普通签名,因为它们都具有易于生成但其他人难以伪造的优点。数字签 名可以永久绑定到被签名消息的内容,
在数字签名系统中,一方面,消息通常很长,但另一方面,我们必须使用公钥密码系统,在处理长消息时效率很低。解决方案是通过哈希函数创 建消息的摘要,例如,产生比消息小得多的校验和。因此,发送方首先生成一个摘要,然后使用自己的私钥对其进行加密以生成签名,然后将签 名与消息一起发送给接收方。在接收方,将签名者的公钥应用于签名以获得传输的摘要,摘要也是直接从消息中确定的。如果两个摘要相同,则 只有给定的发送器可以发出消息并且该肖息保持其完整性。
重要的是要强调私钥和公钥在数字签名中的使用方式与密码学中保密性的区别。在数字签名中,签名者 transmitter使用签名者的私钥和验证者 对消息摘要进行签名receiver使用签名者的公钥进行验证。相反,在密码学中,接收方的公钥和私钥用于该过程。
公钥密码学的另一个重要应用是数字信封。数字信封是数据加密的框架,其中数据使用私钥密码术 (例如 DES 或AES) 在秘密密钥下加密,而此 秘密密钥使用公钥密码术 (例如 RSA) 加密,并且发送给对方。简而言之,公钥加密可用于将私钥分发给希望通信的成对个人。

数学代写|离散数学代写Discrete Mathematics代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
微观经济学代写
微观经济学是主流经济学的一个分支,研究个人和企业在做出有关稀缺资源分配的决策时的行为以及这些个人和企业之间的相互作用。my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学Mathematics代写服务。我们的专家在图论代写Graph Theory代写方面经验极为丰富,各种图论代写Graph Theory相关的作业也就用不着 说。
线性代数代写
线性代数是数学的一个分支,涉及线性方程,如:线性图,如:以及它们在向量空间和通过矩阵的表示。线性代数是几乎所有数学领域的核心。
博弈论代写
现代博弈论始于约翰-冯-诺伊曼(John von Neumann)提出的两人零和博弈中的混合策略均衡的观点及其证明。冯-诺依曼的原始证明使用了关于连续映射到紧凑凸集的布劳威尔定点定理,这成为博弈论和数学经济学的标准方法。在他的论文之后,1944年,他与奥斯卡-莫根斯特恩(Oskar Morgenstern)共同撰写了《游戏和经济行为理论》一书,该书考虑了几个参与者的合作游戏。这本书的第二版提供了预期效用的公理理论,使数理统计学家和经济学家能够处理不确定性下的决策。
微积分代写
微积分,最初被称为无穷小微积分或 “无穷小的微积分”,是对连续变化的数学研究,就像几何学是对形状的研究,而代数是对算术运算的概括研究一样。
它有两个主要分支,微分和积分;微分涉及瞬时变化率和曲线的斜率,而积分涉及数量的累积,以及曲线下或曲线之间的面积。这两个分支通过微积分的基本定理相互联系,它们利用了无限序列和无限级数收敛到一个明确定义的极限的基本概念 。
计量经济学代写
什么是计量经济学?
计量经济学是统计学和数学模型的定量应用,使用数据来发展理论或测试经济学中的现有假设,并根据历史数据预测未来趋势。它对现实世界的数据进行统计试验,然后将结果与被测试的理论进行比较和对比。
根据你是对测试现有理论感兴趣,还是对利用现有数据在这些观察的基础上提出新的假设感兴趣,计量经济学可以细分为两大类:理论和应用。那些经常从事这种实践的人通常被称为计量经济学家。
Matlab代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。