MY-ASSIGNMENTEXPERT™可以为您提供my.uq.edu PHYS4040 Quantum field theory量子场论课程的代写代考和辅导服务!
这是昆士兰大学 量子场论课程的代写成功案例。
PHYS4040课程简介
Course Description: This course covers advanced topics from single-particle quantum mechanics, such as advanced quantum dynamics, path-integrals, and quantum decoherence. It will also cover introductory non-relativistic many-body quantum theory, relativistic quantum mechanics, and relativistic quantum field theory. We will look at selected applications from atom optics, condensed matter physics, and particle physics.
Assumed Background:
Students should have a sound understanding of quantum physics at the level of PHYS3040 (or equivalent). Background in special relativity (e.g. PHYS2100), electromagnetic fields (e.g. PHYS3051), condensed matter physics (e.g. PHYS2020) and statistical mechanics (e.g. PHYS3020) is strongly recommended.
Prerequisites
This course aims at a first introduction to relativistic quantum field theory. This plays a fundamental role in our understanding of particle physics but arises also in the study of statistical mechanics and second quantised condensed matter systems.
Course Changes in Response to Previous Student Feedback
The course has been modified to be more interactive, with more chance for students to work through problems with assistance.
PHYS4040 Quantum field theory HELP(EXAM HELP, ONLINE TUTOR)
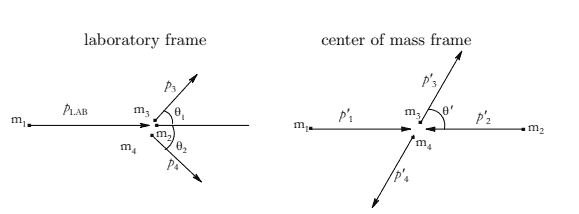
The conservation of four-momentum implies that in particle one’s rest frame,
$$
p_1^0=m_1=E_2+E_3 .
$$
By the invariance of $p_1^2, p_2^2$, and $p_3^2$, it is clear that,
$$
\begin{aligned}
p_1^2=m_1^2 & =\left(p_2+p_3\right)^2, \
& =p_2^2+p_3^2+2 p_2 p_3, \
& =m 2^2+m_3^2+2 E_2 E_3-\vec{p}_2 \overrightarrow{p_3} .
\end{aligned}
$$
But in particle one’s rest frame, $\vec{p}_2=-\vec{p}_3$ and by (1.1), $E_3=m_1-E_2$. Therefore,
$$
\begin{gathered}
m_1^2=m_2^2+m_3^2+2 m_1 E_2-2\left(E_2^2-\vec{p}_2^2\right), \
=m_3^2-m_2^2+2 m_1 E_2, \
\therefore E_2=\frac{m_1}{2}+\frac{m_2^2-m_3^2}{2 m_1} .
\end{gathered}
$$
In the center of mass frame of reference, the total 4-momentum can be described by,
$$
p_{c m}=p_1^{\prime}+p_2^{\prime}=\left(E_1+E_2 ; \overrightarrow{0}\right) \equiv\left(E_{c m} ; \overrightarrow{0}\right)
$$
Note that $p_1 p_2$ is an invariant scalar product. Evaluated in the laboratory frame,
$$
p_1 p_2=E_L m_2-\vec{p}L \overrightarrow{0}=E_L m_2 $$ This allows us to conclude that, $$ \begin{aligned} p{c m}^2 & =E_{c m}^2=p_1^{\prime 2}+p_2^{\prime 2}+2 p_1 p_2, \
\therefore E_{c m}^2 & =m_1^2+m_2^2+2 E_L m_2 .
\end{aligned}
$$
Consider the four-vectors $\eta$ and $\lambda$ defined by,
$$
\begin{array}{rr}
\eta \equiv\left(p_1+p_2\right)=\left(E_L+m_2 ; \vec{p}L\right) & \eta^{\prime} \equiv\left(E_1^{\prime}+E_2^{\prime} ; \overrightarrow{0}\right)=\left(E{c m} ; \overrightarrow{0}\right) \
\lambda \equiv\left(p_1-p_2\right)=\left(E_L-m_2 ; \vec{p}L\right) & \lambda^{\prime} \equiv\left(E_1^{\prime}-E_2^{\prime} ; 2 \vec{p}^{\prime}\right) . \end{array} $$ By the frame-invariance of the scalar product, $$ \eta \lambda=\eta^{\prime} \lambda^{\prime}=E_L^2-m_1^2-\left|\vec{p}_L\right|^2=E{c m}\left(E_1^{\prime}-E_2^{\prime}\right)
$$
Consider two concentric coplanar circles ( $r=$ constant) in Schwarzschild geometry. Suppose that the measured circumferences of these circles are $C_1$ and $C_2$. (a) What is the radial co-ordinate difference $\Delta r$ between these circles? (b) What is the measured radial distance between these two circles? (c) For the sun, take the two circles as having circumferences $C_1=2 \pi R_{\odot}$ and $C_2=4 \pi R_{\odot}$. By how many centimeters does the measured radial distance between them differ from the result expected in flat space?
Now consider the identity $\eta^{\prime 2} \lambda^{\prime 2}=\eta^2 \lambda^2$. Calculating these products and using the result above,
$$
\begin{aligned}
\eta^{\prime 2} \lambda^{\prime 2}=E_{c m}^2\left(\left(E_1^{\prime}-E_2^{\prime}\right)^2-4\left|\vec{p}1^{\prime}\right|^2\right) & =\left(\left(E_L+m_2\right)^2-\left|\vec{p}_L\right|^2\right)\left(\left(E_L-m_2\right)^2-\left|\vec{p}_L\right|^2\right)=\eta^2 \lambda^2, \ E{c m}^2\left(E_1^{\prime}-E_2^{\prime}\right)^2-4\left|\vec{p}1\right|^2 E{c m}^2 & =\left(E_L^2-m_2^2-\left|\vec{p}L\right|^2\right)^2-4 m_2^2\left|\vec{p}_L\right|^2, \ & =E{c m}^2\left(E_1^{\prime}-E_2^{\prime}\right)^2-4 m_2^2\left|\vec{p}L\right|^2, \ \therefore\left|\vec{p}_1^{\prime}\right|^2=\frac{m_2^2\left|\vec{p}_L\right|^2}{E{c m}^2} & \Rightarrow\left|\vec{p}1\right|=\frac{m_2\left|\vec{p}_L\right|}{E{c m}} .
\end{aligned}
$$
(d) By the conservation of four-momentum, $q=p_1-p_3=p_4-p_2$. So,
$$
\begin{aligned}
q^2=\left(p_4-p_2\right)^2 & =2 m_4^2-2 p_2 p_4 \
& =2 m_4^2-2 E_4 m_4 \
\therefore q^2 & =-2 m_4\left(E_4-m_4\right) .
\end{aligned}
$$
The first part of this problem, namely that $s \equiv\left(p_1+p_2\right)^2=E_{c m}^2$, was demonstrated and used in part (b) above. Let us now consider $t \equiv q^2$,
$$
t \equiv q^2=p_1^2+p_3^2-2 p_1 p_3=2 m_1^2-2 E_1^{\prime} E_3^{\prime}+2\left|\vec{p}_1^{\prime}\right|\left|\vec{p}_3^{\prime}\right| \cos \left(\theta^{\prime}\right)
$$
Here, we wrote $p_1 p_2$ explicitly in the center of mass frame. Because it is an invariant, any frame will do. Now we can use the fact that $m_1=m_3$ and $m_2=m_4$ to see that $\left|\vec{p}_1^{\prime}\right|=\left|\vec{p}_3^{\prime}\right|$ and that $E_1^{\prime}=E_3^{\prime}$ by using part (c) from above. We will now use the notation of the assignment where $\left|\vec{p}_1^{\prime}\right|=p^{\prime}$. This quickly reduces the above equality to
$$
q^2=2\left(m_1^2-E_1^{\prime 2}+p^2 \cos \left(\theta^{\prime}\right)\right) \text {. }
$$
This can be simplified in two ways. First, notice that $m_1^2-E_1^{\prime 2}=-p^{\prime 2}$ because $E_1^{\prime 2}-p^{\prime 2}=$ $m_1^2$. Second we will use the trigonometric identity $1-\cos (\alpha)=2 \sin ^2(\alpha / 2)$. Introducing these simplifications we obtain
$$
q^2=-4 p^2 \sin ^2\left(\theta^{\prime} / 2\right) .
$$

MY-ASSIGNMENTEXPERT™可以为您提供MY.UQ.EDU PHYS4040 QUANTUM FIELD THEORY量子场论课程的代写代考和辅导服务!