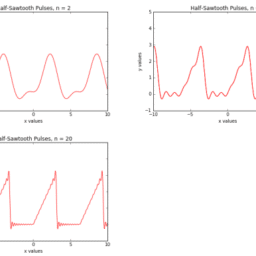
MY-ASSIGNMENTEXPERT™可以为您提供Stanford EE261 Fourier analysis傅里叶分析的代写代考和辅导服务!
这是斯坦福大学 傅里叶分析课程的代写成功案例。
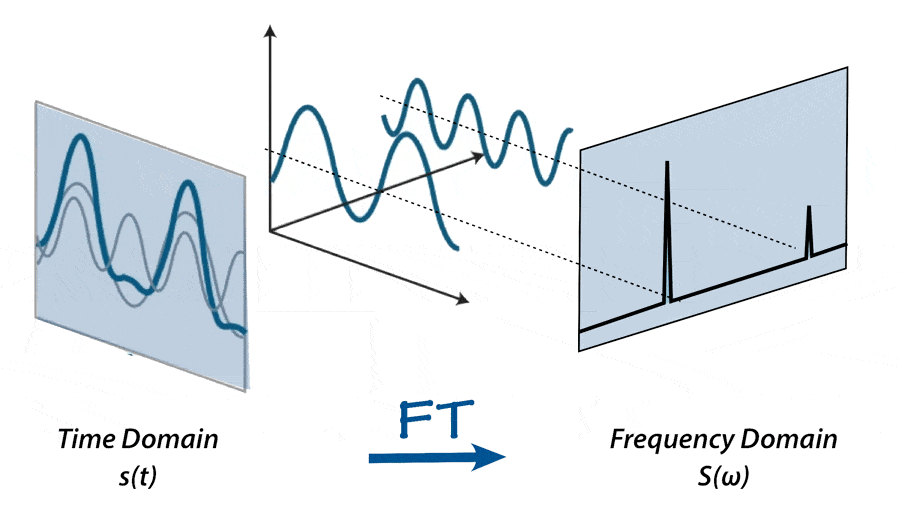
EE261课程简介
The goals for the course are to gain a facility with using the Fourier transform, both specific techniques and general principles, and learning to recognize when, why, and how it is used. Together with a great variety, the subject also has a great coherence, and the hope is students come to appreciate both.
Topics include: The Fourier transform as a tool for solving physical problems. Fourier series, the Fourier transform of continuous and discrete signals and its properties. The Dirac delta, distributions, and generalized transforms. Convolutions and correlations and applications; probability distributions, sampling theory, filters, and analysis of linear systems. The discrete Fourier transform and the FFT algorithm. Multidimensional Fourier transform and use in imaging. Further applications to optics, crystallography. Emphasis is on relating the theoretical principles to solving practical engineering and science problems.
Prerequisites
e goals for the course are to gain a facility with using the Fourier transform, both specific techniques and general principles, and learning to recognize when, why, and how it is used. Together with a great variety, the subject also has a great coherence, and the hope is students come to appreciate both.
Topics include:
- The Fourier transform as a tool for solving physical problems.
- Fourier series, the Fourier transform of continuous and discrete signals and its properties.
- The Dirac delta, distributions, and generalized transforms.
- Convolutions and correlations and applications; probability distributions, sampling theory, filters, and analysis of linear systems.
- The discrete Fourier transform and the FFT algorithm.
- Multidimensional Fourier transform and use in imaging.
- Further applications to optics, crystallography.
- Emphasis is on relating the theoretical principles to solving practical engineering and science problems.
EE261 Fourier analysis HELP(EXAM HELP, ONLINE TUTOR)
The dyadic cubes in $\mathbb{R}^d$ are the sets of the form
$$
Q_{n, k}=\left[k_1 2^n,\left(k_1+1\right) 2^n\right) \times \cdots \times\left[k_d 2^n,\left(k_d+1\right) 2^n\right)
$$
were $n$ ranges over $\mathbb{Z}$ and $k \in \mathbb{Z}^d$.
(a) Given a collection of dyadic cubes whose diameters are bounded, show that one may find a sub-collection which covers the same region of $\mathbb{R}^d$ but with all cubes disjoint.
(b) Define the (uncentered) dyadic maximal function by
$$
\leftM_D f\right=\sup _{Q \ni x} \frac{1}{|Q|} \int_Q f(y) d y
$$
where the supremum is over all dyadic cubes that contain $x$. Show that this operator is of weak type $(1,1)$.
(c) Deduce boundedness of the Hardy-Littlewood maximal function from the above.
Remarks: Part (a) provides a replacement for the Vitali Covering Lemma. I propose you address (c) ‘geometrically’; draw some pictures in the planar $(d=2)$ case.
(a) Evaluate
$$
D_N(x)=\sum_{n=-N}^N e^{2 \pi i n x}
$$
and show that it is not an approximate identity on $\mathbb{T}$.
(b) Show that $\frac{1}{2 N+1}\left|D_N(x)\right|^2$ is an approximate identity and derive its relation to the Fejer kernel.
(c) Calculate
$$
\sum_{n \in \mathbb{Z}} r^{|n|} e^{2 \pi i n x}
$$
for $0<r<1$ and show that for $r \rightarrow 1$ it gives rise to an approximate identity.
(d) Suppose $\phi_n$ is an approximate identity and $d \mu$, a finite complex measure on $\mathbb{T}$.
Show that $\phi_n * d \mu$ converges weak-* to $d \mu$.
Note: $d \mu_n$ converges weak-* to $d \mu$ iff for every bounded continuous function, $f$, $\int f d \mu_n \rightarrow \int f d \mu$
(a) Given $f \in L^p(\mathbb{R}), 1 \leq p<\infty$, show that $t \mapsto f(x+t)$ defines a continuous map of $\mathbb{R}$ into $L^p(\mathbb{R}, d x)$.
(b) Show that it is not equi-continuous as $f$ varies over the set of $f$ with $|f|_{L^p} \leq 1$.
(That is, $\epsilon$ cannot be chosen from $\delta$ independently of $f$.)
(c) Show that part (a) is false for $L^{\infty}$ and $M(\mathbb{R})$.
(From Wolff §4.) Find a sequence of Schwartz functions $\phi_n$ such that (a) $\left|\phi_n\right|_{L^p}$ and $\left|\hat{\phi}n\right|{L^{p^{\prime}}}$ are constant. The supports of $\hat{\phi}n$ are disjoint and those of $\phi_n$ are almost disjoint. Use $\sum{n=1}^N \phi_n$ to show that if $|\hat{f}|_{L^{p^{\prime}}} \lesssim|f|_{L^p}$ then $p \leq 2$.
By almost disjoint we mean $\left|\sum_{n=1}^N \phi_n\right|_{L^p}^p \leq \frac{100}{99} \sum_{n=1}^N\left|\phi_n\right|_{L^p}^p$. Notice that if the supports were actually disjoint, then $100 / 99$ could be replaced by 1 .
Hint: Take a single $C_c^{\infty}$ function and modify it by translation and multiplication by characters.

MY-ASSIGNMENTEXPERT™可以为您提供STANFORD EE261 FOURIER ANALYSIS傅里叶分析的代写代考和辅导服务!