数学代写|MATH5330 Abstract Algebra

For $n=5,8,12,20$, and 25 , find all positive integers less than $n$ and relatively prime to
$n$.

Determine
a. $\operatorname{gcd}(2,10) \quad \operatorname{lcm}(2,10)$
b. $\operatorname{gcd}(20,8) \quad \operatorname{lcm}(20,8)$
c. $\operatorname{gcd}(12,40) \quad \operatorname{lcm}(12,40)$
d. $\operatorname{gcd}(21,50) \quad \operatorname{lcm}(21,50)$
e. $\operatorname{gcd}\left(p^2 q^2, p q^3\right) \quad \operatorname{lcm}\left(p^2 q^2, p q^3\right)$ where $p$ and $q$ are distinct primes

Determine $51 \bmod 13,342 \bmod 85,62 \bmod 15,10 \bmod 15,(82 \cdot 73) \bmod 7,(51+68)$ $\bmod 7,(35 \cdot 24) \bmod 11$, and $(47+68) \bmod 11$.

Find integers $s$ and $t$ such that $1=7 \cdot s+11 \cdot t$. Show that $s$ and $t$ are not unique.

Prove that every integer that is a common multiple of every member of a finite set of integers is a multiple of the least common multiple of those integers.

Prove that for any three consecutive integers $n, n+1, n+2$ one must be divisible by 3 .

Show that if $a$ and $b$ are positive integers, then $a b=\operatorname{lcm}(a, b) \cdot \operatorname{gcd}(a, b)$.

Suppose $a$ and $b$ are integers that divide the integer $c$. If $a$ and $b$ are relatively prime, show that $a b$ divides $c$. Show, by example, that if $a$ and $b$ are not relatively prime, then $a b$ need not divide $c$.

If $a$ and $b$ are integers and $n$ is a positive integer, prove that $a \bmod n=b \bmod n$ if and only if $n$ divides $a-b$.

Let $d=\operatorname{gcd}(a, b)$. If $a=d a^{\prime}$ and $b=d b^{\prime}$, show that $\operatorname{gcd}\left(a^{\prime}, b^{\prime}\right)=1$.

Let $n$ be a fixed positive integer greater than 1. If $a \bmod n=a^{\prime}$ and $b \bmod n=b^{\prime}$, prove that $(a+b) \bmod n=\left(a^{\prime}+b^{\prime}\right) \bmod n$ and $(a b) \bmod n=\left(a^{\prime} b^{\prime}\right) \bmod n$. (This exercise is referred to in Chapters $6,8,10$, and 15.)

Let $a$ and $b$ be positive integers and let $d=\operatorname{gcd}(a, b)$ and $m=\operatorname{lcm}(a, b)$. If $t$ divides both $a$ and $b$, prove that $t$ divides $d$. If $s$ is a multiple of both $a$ and $b$, prove that $s$ is a multiple of $m$.

Let $n$ and $a$ be positive integers and let $d=\operatorname{gcd}(a, n)$. Show that the equation $a x \bmod$ $n=1$ has a solution if and only if $d=1$. (This exercise is referred to in Chapter 2.)

Show that $5 n+3$ and $7 n+4$ are relatively prime for all $n$.

Suppose that $m$ and $n$ are relatively prime and $r$ is any integer. Show that there are integers $x$ and $y$ such that $m x+n y=r$.

Let $p, q$, and $r$ be primes other than 3 . Show that 3 divides $p^2+q^2+r^2$.

Prove that every prime greater than 3 can be written in the form $6 n+1$ or $6 n+5$.

Determine $7^{1000} \bmod 6$ and $6^{1001} \bmod 7$.

Let $a, b, s$, and $t$ be integers. If $a \bmod s t=b \bmod s t$, show that $a \bmod s=b \bmod s$ and $a \bmod t=b \bmod t$. What condition on $s$ and $t$ is needed to make the converse true? (This exercise is referred to in Chapter 8.)

If $n$ is an integer greater than 1 and $(n-1) !=1 \bmod n$, prove that $n$ is prime.

Show that $\operatorname{gcd}(a, b c)=1$ if and only if $\operatorname{gcd}(a, b)=1$ and $\operatorname{gcd}(a, c)=1$. (This exercise is referred to in Chapter 8.)

Let $p_1, p_2, \ldots, p_n$ be primes. Show that $p_1 p_2 \cdots p_n+1$ is divisible by none of these primes.

Prove that there are infinitely many primes. (Hint: Use Exercise 22.)

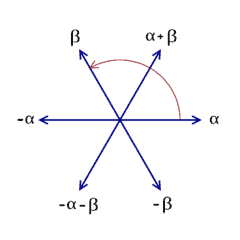
For any complex numbers $z_1$ and $z_2$, prove that $\left|z_1 z_2\right|=\left|z_1\right|\left|z_2\right|$.