MY-ASSIGNMENTEXPERT™可以为您提供ucsd.edu Math280A Probability Theory概率论课程的代写代考和辅导服务!
这是加利福尼亚大学圣迭戈分校概率论课程的代写成功案例。
Math280A课程简介
Math 280A is the first quarter of a three-quarter graduate level sequence in the theory of probability. This sequence provides a rigorous treatment of probability theory, using measure theory, and is essential preparation for Mathematics PhD students planning to do research in probability. A strong background in undergraduate real analysis at the level of Math 140AB is essential for success in Math 280A. In particular, students should be comfortable with notions such as countable and uncountable sets, limsup and liminf, and open, closed, and compact sets, and should be proficient at writing rigorous epsilon-delta style proofs. Graduate students who do not have this preparation are encouraged instead to consider Math 285, a one-quarter course in stochastic processes which will be offered in Winter 2021. See also this page, maintained by Ruth Williams, for more information on graduate courses in probability at UCSD.
Prerequisites
According to the UC San Diego Course Catalog, the topics covered in the full-year sequence 280ABC include the measure-theoretic foundations of probability theory, independence, the Law of Large Numbers, convergence in distribution, the Central Limit Theorem, conditional expectation, martingales, Markov processes, and Brownian motion. Given the current pandemic crisis and emergency remote teaching modality, it is more difficult than usual to predict what pace we will work through this material, and where the dividing line between 280A and 280B will occur.
Math280A Probability Theory HELP(EXAM HELP, ONLINE TUTOR)
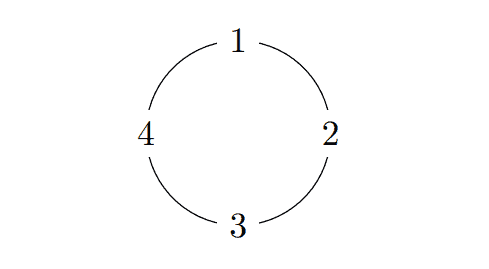
Four people are seated around a table as in the diagram below. Another clumsy person accidentally spills water on two adjacent people at the table. (For example, the water could be spilled on 1 and 2 , or on 1 and 4 , but not on 1 and 3.) The clumsy person is equally likely to spill water on any of the four adjacent pairs.
Let $W_1$ be the event “person 1 had water spilled on them”. Define $W_2, W_3, W_4$ similarly.
(a) Which pairs of the events $W_1, W_2, W_3, W_4$ are independent? Explain why.
(b) Which pairs of the events $W_1, W_2, W_3, W_4$ are disjoint? Explain why.
You operate a polar research station; every morning, you send a radio message indicating which way the wind is blowing. The wind is likely to blow in any of 4 directions, which you indicate with the codewords “000”, “110”, “101”, and “011”.
Due to the extreme weather, each bit ( 0 or 1$)$ of the message independently has a $\frac{1}{3}$ chance of being flipped in transit: 1 changed to 0 or vice versa.
What is the probability that when you send your message, the recipient receives “111” on their end?
You are waiting for a bus at a bus stop. There are actually two buses that stop here. The one you want will arrive at a uniformly random time within the next 30 minutes. There is also a different bus, which will arrive at a uniformly random time within the next 60 minutes.
Given that exactly one of the buses arrives within the next 5 minutes, what is the probability that it is the one you want?
Note: we want a conditional probability here-and in the next two problems, as well.
You find a 6-sided die on the ground. For no reason in particular, you decide to roll it. After you roll it three times, you discover something peculiar: every time, the die has landed on the side labeled :i. (4). You get suspicious: what if this is an extremely biased die that always lands on 4 ?
(a) What extra piece of information would you need to calculate, given your experimental data, how likely this die is to be an “extremely biased” die that always lands on 4 ?
(b) Come up with a plausible value for this extra piece of information, and use it to compute that probability.
Suppose you live in an extremely unfortunate climate where it always rains on weekends (Saturday and Sunday). For that matter, there is always a $\frac{1}{2}$ chance of rain on a weekday (Monday-Friday) as well.
If you have completely forgotten which day of week it is (so that it is equally likely to be any of the seven days), but you go outside and see that it’s raining, what is the probability that it’s the weekend?

MY-ASSIGNMENTEXPERT™可以为您提供UCSD.EDU MATH280A PROBABILITY THEORY概率论课程的代写代考和辅导服务!