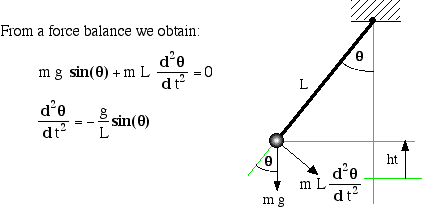MY-ASSIGNMENTEXPERT™可以为您提供stanford Math220 Ordinary Differential Equations常微分方程的代写代考和辅导服务!
这是斯坦福大学 常微分方程课程的代写成功案例。
Math220课程简介
Grading policy: The grade will be based on the weekly homework (25%), on the in-class midterm exam (30%) and on the in-class (i.e. not take-home, to take place during finals week, as designated by the registrar) final exam (45%).
The homework will be due in class or in the instructor’s mailbox by 9am on the designated day, which will usually (but not always) be Fridays. You are allowed to discuss the homework with others in the class, but you must write up your homework solution by yourself. Thus, you should understand the solution, and be able to reproduce it yourself. This ensures that, apart from satisfying a requirement for this class, you can solve the similar problems that are likely to arise on the exams.
Prerequisites
Course Description : We will cover most of the textbook. This includes formulating physical systems as differential equations, learning various methods to solve them, basics of infinite series and how to use them to solve differential equations, studying linear and nonlinear systems of differential equations, and topological methods.
Learning Outcomes:: The broad learning goals of the course are:
Model various physical phenomena with differential equations
Understand that solutions to differential equations can be addressed with both exact methods and qualitative methods
Math220 Ordinary Differential Equations HELP(EXAM HELP, ONLINE TUTOR)
Exercise 1.1.1. (Frictionless spring) Consider a time varying population of organisms $P(t)$ living in a closed environment (possibly a petri dish). The initial population at time $t=0$ is $P(0)=p_0$. The population in the dish at future times is governed by the logistic model
$$
\frac{d}{d t} P(t)=k P(t)-\frac{k}{K} P(t)^2
$$
where $k>0$ is the reproductive rate of the species and $K>0$ is the carrying capacity of the environment.
- Solve the equation analytically.
- What is the limiting value of $P(t)$ ?
- If the initial population in the dish is $p_0=10$, the reproductive rate is $k=2$ and the carrying capacity is $K=1000$, at what time $t>0$ does the population double? Tripple? Ten times its initial value?
- Suppose that the initial population is very small compared to the carrying capacity. Derive a simplified model of the population growth. Explain what happens to the population size as time goes on (i.e. why was the Reverend Dr. Malthus so worried after he forgot to include the $P^2$ term in his analysis?)
Exercise 1.1.2. (Frictionless spring) Recall Hook’s law, which describes the force exerted on a mass attached to the end of a stretched spring
$$
F(x)=-K x
$$
where $K$ is the “stiffness” constant of the spring, and $x$ is the signed displacement from the equilibrium position of the spring.
- Let the object have mass $m>0$. Use Newton’s laws to derive the equation of motion for the system consisting of a mass connected to a spring, moving freely on a frictionless table top (perhaps a surface of ice or perhaps the mass is attached to well oiled wheels/bearings).
- Suppose that the mass is held motionless at an initial position $x(0)=a$, and that at time $t=0$ the mass is released. Describe the motion of the system for all future time. What is the frequency of the systems oscillation?
- Suppose that the mass is initially at rest in the equilibrium position $x=0$, and that at time $t=0$ the system is “kicked”, imbuing the mass with an initial velocity of $x^{\prime}(0)=b$. Describe the motion of the system for all future time. What is the frequency of the systems oscillation?
Exercise 1.1.3. (Spring with friction) Consider the same setup as in the previous problem, but now suppose that we account for friction between the table and the mass (or friction in the wheels). A typical model of friction is to assume that the force of friction is proportional to the magnitude of the velocity, acting against the direction of motion. (So the faster the object moves the more friction “tries to slow it down”).
- Let the object have mass $m>0$. Use Newton’s laws to derive the equation of motion for the system consisting of a mass connected to a spring, moving on a table top, subject to the force of friction described above. Suppose that the proportionality coefficient of the friction is $C>0$.
- Suppose that the mass is held motionless at an initial position $x(0)=a$, and that at time $t=0$ the mass is released. Describe the motion of the system for all future time.
- Suppose that the mass is initially at rest in the equilibrium position $x=0$, and that at time $t=0$ the system is “kicked”, imbuing the mass with an initial velocity of $x^{\prime}(0)=b$. Describe the motion of the system for all future time.
Exercise 1.1.4. Derive Kepler’s laws from Newton’s laws and the law of universal graviton. Consider only two bodies. (Try this problems for a few minutes/a few hours before you look up the solution online).

MY-ASSIGNMENTEXPERT™可以为您提供STANFORD MATH220 ORDINARY DIFFERENTIAL EQUATIONS常微分方程的代写代考和辅导服务!