MY-ASSIGNMENTEXPERT™可以为您提供sydney MATH5340 Topology代数拓扑的代写代考和辅导服务!
这是悉尼大学代数拓扑课程的成功案列。
MATH5340课程简介
Topology is the mathematical theory of the “shape of spaces”. It gives a flexible framework in which the fabric of space is like rubber and thus enables the study of the general shape of a space. The spaces often arise indirectly: as the solution space of a set of equations; as the parameter space for a family of objects; as a point cloud from a data set; and so on. This leads to strong interactions between topology and a plethora of mathematical and scientific areas. The love of the study and use of topology is far reaching, including the use of topological techniques in the phases of matter and transition which received the 2016 Nobel Prize in Physics. This unit introduces you to a selection of topics in pure or applied topology. Topology receives strength from its areas of applications and imparts insights in return. A wide spectrum of methods is used, dividing topology into the areas of algebraic, computational, differential, geometric and set-theoretic topology. You will learn the methods, key results, and role in current mathematics of at least one of these areas, and gain an understanding of current research problems and open conjectures in the field.
Prerequisites
At the completion of this unit, you should be able to:
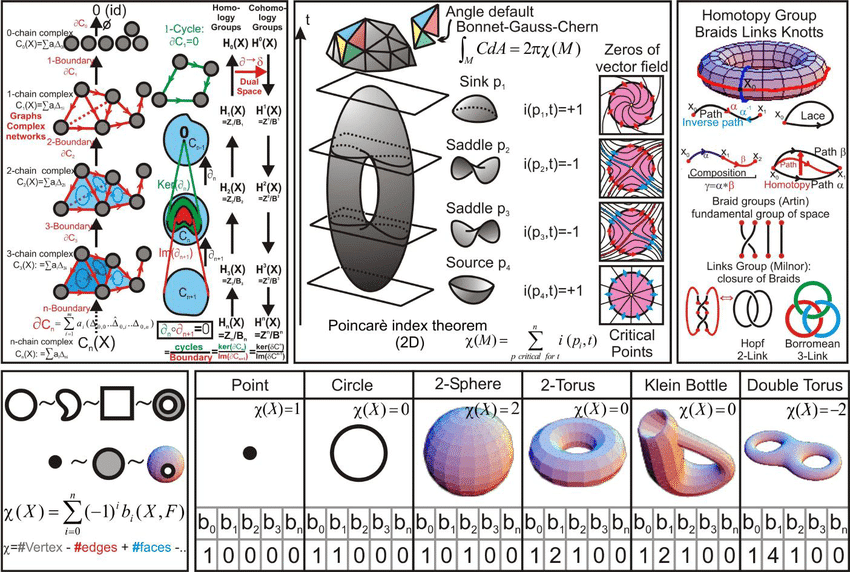
- LO1. Demonstrate a coherent and advanced understanding of the key concepts of fundamental group, covering spaces, homology and cohomology.
- LO2. Apply the fundamental principles and results of algebraic topology to solve given problems.
- LO3. Distinguish and compare the properties of different types of topological spaces and maps between them.
- LO4. Formulate topological problems in terms of algebraic invariants and determine the appropriate framework to solve them.
- LO5. Communicate coherent mathematical arguments appropriately to student and expert audiences, both orally and through written work.
- LO6. Devise computational solutions to complex problems in algebraic topology.
- LO7. Compose correct proofs of unfamiliar general results in algebraic topology.
MATH5340 Algebraic topology HELP(EXAM HELP, ONLINE TUTOR)
Use the principle of recursive definition to show that for any real number x there is a bijection g: \mathbb{N} \rightarrow \mathbb{N} such that
\lim {n \rightarrow \infty} \sum{i=1}^n \frac{(-1)^{g(i)}}{g(i)}=x
Denoting by P, D \subset \mathbb{N} the subsets of even and odd numbers respectively, we define recursively g: \mathbb{N} \rightarrow \mathbb{N} by g(1)=1 and
g(n+1)= \begin{cases}\min (P-{g(1), g(2), \ldots, g(n)}) & \text { if } \sum_{i=1}^n \frac{(-1)^{g(i)}}{g(i)} \leq x \ \min (D-{g(1), g(2), \ldots, g(n)}) & \text { if } \sum_{i=1}^n \frac{(-1)^{g(i)}}{g(i)}>x\end{cases}
As
\sum_{n \in P} \frac{1}{n}=\sum_{n \in D} \frac{1}{n}=+\infty
the map g is bijective and
\lim {n \rightarrow \infty} g(n)=+\infty, \quad \lim {n \rightarrow \infty}\left|\sum_{i=1}^n \frac{(-1)^{g(i)}}{g(i)}-x\right|=0 .
Let X be the set of finite sequences of natural numbers. Prove X is countable.
Hint: call \left{p_n\right} the sequence of primes: p_1=2, p_2=3, p_3=5 and so on. To each finite sequence a_1, \ldots, a_n of natural numbers we can associate the product p_1^{a_1} p_2^{a_2} \cdots p_n^{a_n}
Prove the existence of an infinite, non-countable family of subsets C_i \subset \mathbb{N} such that C_i \cap C_j has finite cardinality for every i \neq j.
Hint: consider, for any real x \in[1,10[, the map
f_x: \mathbb{N} \rightarrow \mathbb{N}, \quad f_x(n)=\left\lfloor 10^n x\right\rfloor,
where \lfloor-\rfloor indicates the integer part: \lfloor t\rfloor=\max {n \in \mathbb{Z} \mid n \leq t}. Prove that \lim _n f_x(n) / 10^n=x, and since 10^n \leq f_x(n)<10^{n+1}, show that x \in[1,10[ is uniquely determined by the range of f_x. Then show that f_x(n)<f_y(n) implies f_x(m)<f_y(m) for any m \geq n.
Let X=\coprod\left{X_i \mid i \in I\right} and Y=\coprod\left{Y_i \mid i \in I\right} be disjoint unions of families indexed by the same set I. If X_i has the cardinality of Y_i for every i \in I, prove that X has the same cardinality of Y.
By the axiom of choice we may choose, for any i \in I, a bijection f_i: X_i \rightarrow Y_i. Now consider the map
f: X \rightarrow Y, \quad f(x)=f_i(x) \text { if } x \in X_i

MY-ASSIGNMENTEXPERT™可以为您提供SYDNEY MATH5340 TOPOLOGY代数拓扑的代写代考和辅导服务!