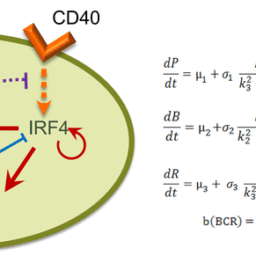
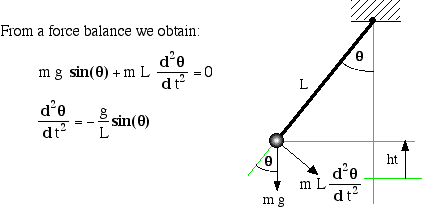MY-ASSIGNMENTEXPERT™可以为您提供stanford Math220 Ordinary Differential Equations常微分方程的代写代考和辅导服务!
这是斯坦福大学 常微分方程课程的代写成功案例。

Math220课程简介
Grading policy: The grade will be based on the weekly homework (25%), on the in-class midterm exam (30%) and on the in-class (i.e. not take-home, to take place during finals week, as designated by the registrar) final exam (45%).
The homework will be due in class or in the instructor’s mailbox by 9am on the designated day, which will usually (but not always) be Fridays. You are allowed to discuss the homework with others in the class, but you must write up your homework solution by yourself. Thus, you should understand the solution, and be able to reproduce it yourself. This ensures that, apart from satisfying a requirement for this class, you can solve the similar problems that are likely to arise on the exams.
Prerequisites
Course Description : We will cover most of the textbook. This includes formulating physical systems as differential equations, learning various methods to solve them, basics of infinite series and how to use them to solve differential equations, studying linear and nonlinear systems of differential equations, and topological methods.
Learning Outcomes:: The broad learning goals of the course are:
Model various physical phenomena with differential equations
Understand that solutions to differential equations can be addressed with both exact methods and qualitative methods
Math220 Ordinary Differential Equations HELP(EXAM HELP, ONLINE TUTOR)
One aims to determine the time of death of a homicide victim. The body was found with a temperature of $85^{\circ} \mathrm{F}$ at $12 \mathrm{~h} 00 \mathrm{PM}$ in a closed room, which has a constant temperature of $72^{\circ} \mathrm{F}$. Three hours later, the temperature of the body was measured in the same room and it was $78^{\circ} \mathrm{F}$. Using Fourier’s law of cooling, i.e.
$$
T^{\prime}(t)=k\left(T_{e n v}-T(t)\right)
$$
where $k$ is a positive constant, find the time of death knowing also that at this time the victim had a normal body temperature of $98.6^{\circ} \mathrm{F}$.
Find the general solution of each of the following equations:
(1) $16 y^{\prime \prime}-8 y^{\prime}+y=0$
(2) $y^{\prime \prime}+4 y^{\prime}+5 y=0$
(3) $y^{\prime \prime}+4 y^{\prime}-5 y=0$
(4) $y^{\prime \prime}-6 y^{\prime}+9 y=(x+1) e^{3 x}$
(5) $y^{\prime \prime \prime}-6 y^{\prime \prime}+13 y^{\prime}-10 y=e^{2 x} \cos (x)$
Consider a linear homogeneous ODE of the form $T[y]=0$, where the differential operator $T$ is given as
$$
T[y]=y^{\prime \prime}+a(x) y^{\prime}+b(x) y
$$
for some functions $a(x), b(x)$.
(1) Prove that if $y_1(x)$ and $y_2(x)$ are two solutions of the given homogeneous equation, then so is every linear combination $c_1 y_1(x)+c_2 y_2(x)$ of $y_1, y_2$ by scalars $c_1, c_2 \in \mathbb{R}$.
(2) Let $f(x)$ be another function. Consider now a non-homogeneous equation
$$
T[y]=f(x)
$$
Suppose that $y_p(x)$ is a particular solution of the new equation. Prove that every other solution of $T[y]=f(x)$ is of the form $y=y_p+y_h$, where $y_h$ is a solution of the associated homogeneous equation.
If $y_1(x)$ and $y_2(x)$ are solutions of
$$
y^{\prime \prime}+P(x) y^{\prime}+Q(x) y=R_1(x)
$$
and
$$
y^{\prime \prime}+P(x) y^{\prime}+Q(x) y=R_2(x),
$$
show that $y(x)=y_1(x)+y_2(x)$ is a solution of
$$
y^{\prime \prime}+P(x) y^{\prime}+Q(x) y=R_1(x)+R_2(x)
$$
This is called the principle of superposition. Use this principle to find the general solution of $y^{\prime \prime}+9 y=$ $2 \sin 3 x+4 \sin x-26 e^{-2 x}+27 x^3$
(1) Show that the Laplace transform of the function $f:(0,+\infty) \rightarrow(0,+\infty), f(x)=1 / x$ does not exists. Hint: estimate $e^{-p x}$ from below by a constant when $x \in[\varepsilon, 1], 0<\varepsilon<1$.
(2) Find a function which has the Laplace transform $1 /\left(p^2+p^4\right)$.
(3) Find the Laplace transforms of $\sin ^2(a x)$ and $\cos ^2(a x)$ only using the Laplace transform of $\cos (b x)$ and constants, but no integration. Hint: write two trigonometric formulas linking the previous two functions.
(4) Find the Laplace transform of $f:[0,+\infty) \rightarrow \mathbb{R}$ defined as $f(x)=\sin (x)$ if $x \in[0, \pi]$ and $f(x)=0$ if $x>\pi$.

MY-ASSIGNMENTEXPERT™可以为您提供STANFORD MATH220 ORDINARY DIFFERENTIAL EQUATIONS常微分方程的代写代考和辅导服务!