MY-ASSIGNMENTEXPERT™可以为您提供sites.google MA307 Riemann surface黎曼曲面课程的代写代考和辅导服务!
这是印度科學理工學院黎曼曲面课程的代写成功案例。
MA307课程简介
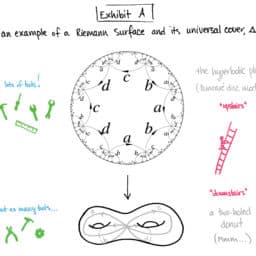
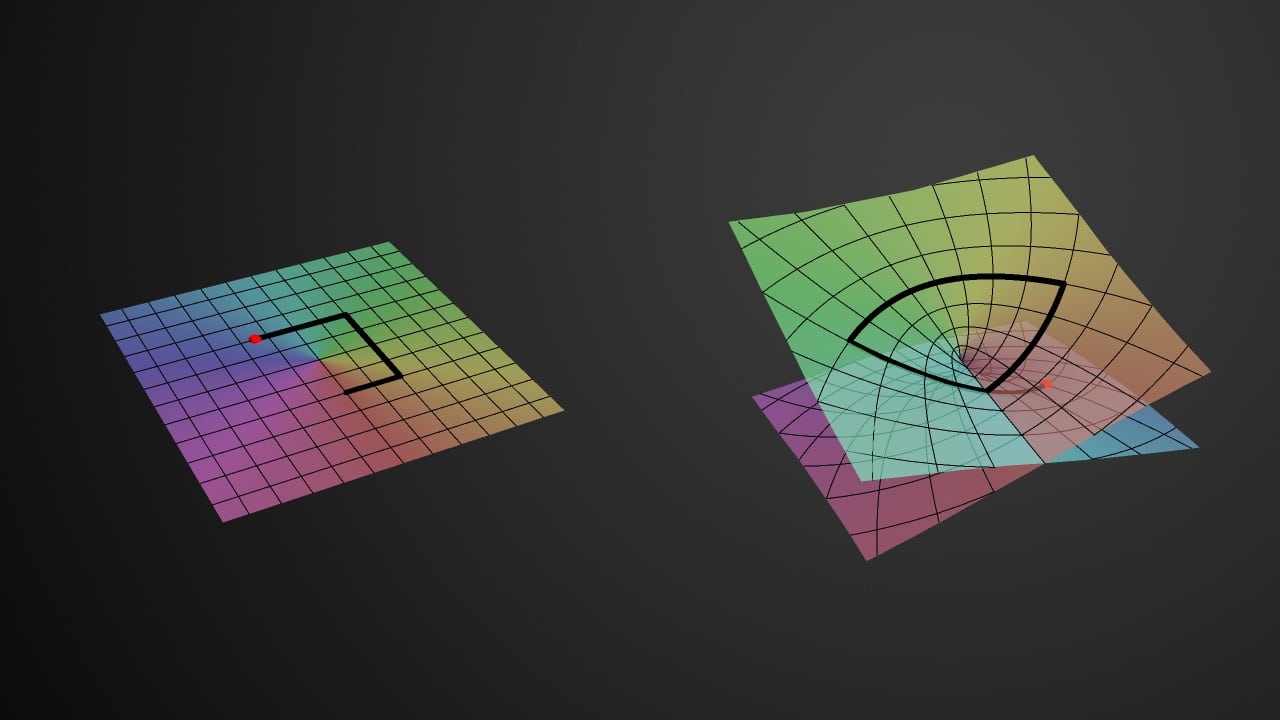
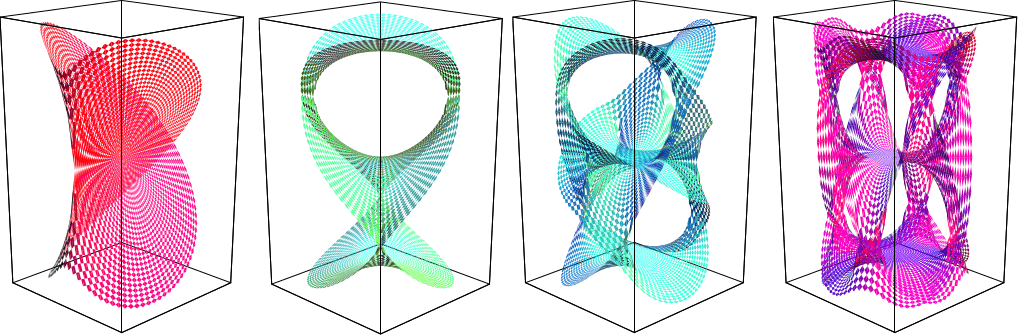
Course description: Riemann surfaces are one-dimensional complex manifolds, obtained by gluing together pieces of the complex plane by holomorphic maps. This course will be an introduction to the the theory of Riemann surfaces, with an emphasis on analytical and topological aspects. After describing examples and constructions of Riemann surfaces, the topics covered would include branched coverings and the Riemann-Hurwitz formula, holomorphic 1-forms and periods, the Weyl’s Lemma and existence theorems, the Hodge decomposition theorem, Riemann’s bilinear relations, Divisors, the Riemann-Roch theorem, theorems of Abel and Jacobi, the Uniformization theorem, Fuchsian groups and hyperbolic surfaces.
Prerequisites
There will be no class on January 5th (Tuesday).
There will be no class on December 17th (Thursday).
There will be no class on November 19th (Thursday). Also, no lectures would be held in the midterm week of Nov 23 -27.
A new Teams code has been emailed to the mailing list.
There will be weekly homework also.
There will be no lecture on Tuesday, October 6th.
Lectures will be held on Tuesdays and Thursdays, 3:30-5pm.
Our first meeting will be held on Thursday October 1st , 3:30-5pm.
Classes will be online, at the beginning over Microsoft Teams. The first meeting link will be put up here, and on the IISc Intranet Bulletin board, before the meeting time.
MA307 Riemann surface HELP(EXAM HELP, ONLINE TUTOR)
Let $X=\left{[x: y: z] \in \mathbb{C P}^2 \mid x^3 y+y^3 z+z^3 x=0\right}$ be the smooth projective curve we saw in Homework 1 (it’s called the Klein’s quartic).
(a) Let $\eta=e^{i 2 \pi / 7}$. Show that the map $F: X \rightarrow X$ given by $[x: y$ : $z] \mapsto\left[\eta^2 x: \eta y: \eta^4 z\right]$ is well-defined and a biholomorphism.
(b) Assume that the quotient space $Y=X / \sim$ where $x \sim F(x)$ for all $x \in X$, is a Riemann surface, and the quotient map $\pi: X \rightarrow Y$ is a holomorphic map. Compute the degree of $\pi$, and find its ramification points and their multiplicities.
(c) From the degree-genus formula, it follows that $X$ has genus 3 . Using the Riemann-Hurwitz formula, and your answer in (b), guess what Riemann surface $Y$ is.
Let $\Lambda=\langle z \mapsto z+1, z+i\rangle$ and let $X=\mathbb{C} / \Lambda$. Let $[0] \in X$ be the point corresponding to the $\Lambda$ orbit of $0 \in \mathbb{C}$, and let Aut $_0(X)$ be the group of automorphisms (biholomorphisms) of $X$ that fix $[0]$.
(a) What are the elements of $\operatorname{Aut}_0(X)$ ? (Each such automorphism lifts to an automorphism of $\mathbb{C}$, which is an affine map; determine those affine maps.)
(b) The group $\operatorname{Aut}_0(X)$ acts on $X$ – what is the quotient Riemann surface $X / \operatorname{Aut}_0(X)$ ?
Let $X$ be the hyperelliptic curve defined by the zero set of the (homogenization) of $f(x, y)=y^2-3 x^8-10 x^4-3$, and let $Y$ be the hyperelliptic curve defined by the zero set of the (homogenization) of $g(z, w)=w^2-z^6+1$. Let $X_3$ and $Y_3$ be the corresponding affine curves (i.e. the zero sets of $f$ and $g$ respectively).
(a) Show that the function $f: X_3 \rightarrow Y_3$ defined by
$$
f(x, y)=\left(\left(1+x^2\right) /\left(1-x^2\right), 2 x y /\left(1-x^2\right)^3\right)
$$
extends to a holomorphic map $F: X \rightarrow Y$ of degree 2 which is nowhere ramified.
(b) What is the genus of $X$ and $Y$ ? You need not give a justification for your answer. (Note that the degree-genus formula would not apply since the homogenized polynomials are not nonsingular!)
In the problems below, suppose $X=\mathbb{C} / \Lambda$ where $\Lambda$ is the subgroup of translations corresponding to the lattice generated by $\omega_1, \omega_2$ (that are linearly independent over $\mathbb{R}$ ), exactly as in class. Moreover, let $\mathcal{P}$ be the Weierstrass function on $X$.
Suppose $f$ is an elliptic function on $X$ of degree $d$, and let $A$ be the set of points $c \in \mathbb{C P}^1$ such that $f(z)=c$ has strictly less than $d$ distinct solutions. Show that $A$ is non-empty and finite.
Show that $g(z):=\mathcal{P}^{\prime \prime}(z)-6(\mathcal{P}(z))^2$ is a constant function.
Show that if $f: X \rightarrow \mathbb{C} P^1$ is a holomorphic map (i.e. an elliptic function) of degree two, then
$$
f(z)=\frac{a \mathcal{P}(z-\alpha)+b}{c \mathcal{P}(z-\alpha)+d}
$$
for some $a, b, c, d, \alpha \in \mathbb{C}$ such that $a d-b c=1$.

MY-ASSIGNMENTEXPERT™可以为您提供SITES.GOOGLE MA307 RIEMANN SURFACE交换代数课程的代写代考和辅导服务!