如果你也在 怎样代写组合学Combinatorics 这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。组合学Combinatorics是数学的一个领域,主要涉及计数(作为获得结果的手段和目的)以及有限结构的某些属性。主要涉及计数,作为获得结果的手段和目的,以及有限结构的某些属性。它与数学的许多其他领域密切相关,有许多应用,从逻辑学到统计物理学,从进化生物学到计算机科学。
组合学Combinatorics因其解决的问题的广泛性而闻名。组合问题出现在纯数学的许多领域,特别是在代数、概率论、拓扑学和几何学中,以及在其许多应用领域。许多组合问题在历史上被孤立地考虑,对某个数学背景下出现的问题给出一个临时性的解决方案。然而,在二十世纪后期,强大而普遍的理论方法被开发出来,使组合学本身成为一个独立的数学分支。组合学最古老和最容易理解的部分之一是图论,它本身与其他领域有许多自然联系。在计算机科学中,组合学经常被用来获得算法分析中的公式和估计。
组合学Combinatorics代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。 最高质量的组合学Combinatorics作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此组合学Combinatorics作业代写的价格不固定。通常在专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
同学们在留学期间,都对各式各样的作业考试很是头疼,如果你无从下手,不如考虑my-assignmentexpert™!
my-assignmentexpert™提供最专业的一站式服务:Essay代写,Dissertation代写,Assignment代写,Paper代写,Proposal代写,Proposal代写,Literature Review代写,Online Course,Exam代考等等。my-assignmentexpert™专注为留学生提供Essay代写服务,拥有各个专业的博硕教师团队帮您代写,免费修改及辅导,保证成果完成的效率和质量。同时有多家检测平台帐号,包括Turnitin高级账户,检测论文不会留痕,写好后检测修改,放心可靠,经得起任何考验!
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
我们在数学Mathematics代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学Mathematics代写服务。我们的专家在组合学Combinatorics代写方面经验极为丰富,各种组合学Combinatorics相关的作业也就用不着 说。
数学代写|组合学代写Combinatorics代考|Cutting a Cube
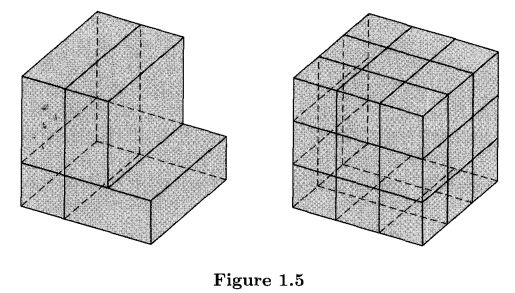
Consider a block of wood in the shape of a cube, 3 feet on an edge. It is desired to cut the cube into 27 smaller cubes, 1 foot on an edge. What is the smallest number of cuts in which this can be accomplished? One way of cutting the cube is to make a series of 6 cuts, 2 in each direction, while keeping the cube in one block as shown in Figure 1.5. But is it possible to use fewer cuts if the pieces can be rearranged between cuts? An example is also given in Figure 1.5 where the second cut now cuts through more wood than it would have if we had not rearranged the pieces after the first cut. Since the number of pieces, and thus the number of rearrangements, increases with each cut, this might appear to be a difficult problem to analyze.
But let us look at it another way. Every one of the 27 small cubes except the one in the middle has at least one face that was originally part of one of the faces of the large cube. The cube in the middle has every one of its faces formed by cuts. Since it has 6 faces, 6 cuts are necessary to form it. Thus, at least 6 cuts are always necessary, and rearranging between cuts does not help. An energetic student might wish to investigate the number of different ways in which the cube can be cut into 27 smaller cubes, using only 6 cuts.
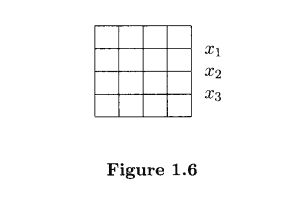
Another example, which combines features of Example 1.1 and the cube-cutting example, is the following: Consider a 4-by-4 chessboard that is perfectly covered with 8 dominoes. Show that it is always possible to cut the board into two nonempty horizontal pieces or two nonempty vertical pieces without cutting through one of the 8 dominoes. The horizontal or vertical line of such a cut is called a fault-line of the perfect cover. Suppose there is a perfect cover of a 4-by-4 board such that none of the three horizontal lines and three vertical lines that cut the board into two nonempty pieces is a fault-line. Let $x_1, x_2$, and $x_3$ be, respectively, the number of dominoes that are cut by the horizontal lines (see Fig. 1.6).
数学代写|组合学代写Combinatorics代考|Magic Squares
Among the oldest and most popular forms of mathematical recreations are magic squares. A magic square of order $n$ is an $n$-by- $n$ array constructed out of the integers $1,2,3, \ldots, n^2$ in such a way that the sum of the integers in each row, in each column, and in each of the two diagonals is the same number $s$. The number $s$ is called the magic sum of the magic square. Examples of magic squares of orders 3 and 4 are
$$
\left[\begin{array}{lll}
8 & 1 & 6 \
3 & 5 & 7 \
4 & 9 & 2
\end{array}\right] \text { and }\left[\begin{array}{rrrr}
16 & 3 & 2 & 13 \
5 & 10 & 11 & 8 \
9 & 6 & 7 & 12 \
4 & 15 & 14 & 1
\end{array}\right]
$$
with magic sums 15 and 34 , respectively. In medieval times there was a certain mysticism associated with magic squares; they were worn for protection against evils. Benjamin Franklin was a magic square fan, and his papers contain many interesting examples.
The sum of all the integers in a magic square of order $n$ is
$$
1+2+3+\cdots+n^2=\frac{n^2\left(n^2+1\right)}{2},
$$
using the formula for the sum of numbers in an arithmetic progression (see Section 7.1). Since a magic square of order $n$ has $n$ rows each with magic sum $s$, we obtain the relation $n s=n^2\left(n^2+1\right) / 2$. Thus, any two magic squares of order $n$ have the same magic sum, namely,
$$
s=\frac{n\left(n^2+1\right)}{2}
$$
组合学代写
数学代写|组合学代写Combinatorics代考|Cutting a Cube
考虑一块立方体形状的木头,边长3英尺。把这个立方体切成27个小方块,每边1英尺。能做到这一点的最小削减是多少?切割立方体的一种方法是连续切割6次,每个方向切割2次,同时将立方体保持在一个块中,如图1.5所示。但是,如果切割之间可以重新排列,是否有可能使用更少的切割?图1.5中也给出了一个例子,如果我们在第一次切割后没有重新排列碎片,那么第二次切割现在会切割更多的木材。由于棋子的数量,以及重新排列的数量,随着每次切割而增加,这似乎是一个难以分析的问题。但是让我们从另一个角度来看。除了中间的那个,27个小立方体中的每一个都至少有一个面原来是大立方体的一个面的一部分。中间的立方体的每一面都是由切割形成的。因为它有6个面,所以需要6个切口来形成它。因此,至少6次切割总是必要的,并且在切割之间重新安排没有帮助。一个精力充沛的学生可能希望研究一下,用6次切,有多少种不同的方法可以把一个立方体切成27个更小的立方体。
另一个例子结合了例1.1的特性和切立方体的例子如下:考虑一个4乘4的棋盘,上面完全覆盖着8张多米诺骨牌。显示它总是有可能切成两个非空的水平块或两个非空的垂直块,而不通过8多米诺骨牌中的一个。这种切割的水平或垂直线称为完美覆盖层的断层线。假设一个4乘4的棋盘有一个完美的覆盖物,使得将棋盘切成两个非空块的三条水平线和三条垂直线中没有一条是断层线。设$x_1, x_2$和$x_3$分别为被水平线切割的多米诺骨牌数量(见图1.6)。
数学代写|组合学代写Combinatorics代考|Magic Squares
在最古老和最流行的数学娱乐形式是魔方。阶为$n$的幻方是一个由整数$1,2,3, \ldots, n^2$组成的$n$ -by- $n$数组,其构造方式使每一行、每一列和两条对角线中的整数之和等于$s$。这个数字$s$被称为幻方的幻和。阶为3和4的幻方的例子有
$$
\left[\begin{array}{lll}
8 & 1 & 6 \
3 & 5 & 7 \
4 & 9 & 2
\end{array}\right] \text { and }\left[\begin{array}{rrrr}
16 & 3 & 2 & 13 \
5 & 10 & 11 & 8 \
9 & 6 & 7 & 12 \
4 & 15 & 14 & 1
\end{array}\right]
$$
,幻和分别为15和34。在中世纪,有一种神秘主义与魔法方块有关;穿它们是为了防止邪恶。本杰明·富兰克林是一个方框迷,他的论文中有许多有趣的例子。
在阶为$n$的幻方中所有整数的和是
$$
1+2+3+\cdots+n^2=\frac{n^2\left(n^2+1\right)}{2},
$$
,使用等差数列中数字和的公式(参见7.1节)。由于阶为$n$的幻方有$n$行,每一行的幻和为$s$,因此我们得到关系$n s=n^2\left(n^2+1\right) / 2$。因此,任意两个阶为$n$的幻方具有相同的幻和,即
$$
s=\frac{n\left(n^2+1\right)}{2}
$$

微观经济学代写
微观经济学是主流经济学的一个分支,研究个人和企业在做出有关稀缺资源分配的决策时的行为以及这些个人和企业之间的相互作用。my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学Mathematics代写服务。我们的专家在图论代写Graph Theory代写方面经验极为丰富,各种图论代写Graph Theory相关的作业也就用不着 说。
线性代数代写
线性代数是数学的一个分支,涉及线性方程,如:线性图,如:以及它们在向量空间和通过矩阵的表示。线性代数是几乎所有数学领域的核心。
博弈论代写
现代博弈论始于约翰-冯-诺伊曼(John von Neumann)提出的两人零和博弈中的混合策略均衡的观点及其证明。冯-诺依曼的原始证明使用了关于连续映射到紧凑凸集的布劳威尔定点定理,这成为博弈论和数学经济学的标准方法。在他的论文之后,1944年,他与奥斯卡-莫根斯特恩(Oskar Morgenstern)共同撰写了《游戏和经济行为理论》一书,该书考虑了几个参与者的合作游戏。这本书的第二版提供了预期效用的公理理论,使数理统计学家和经济学家能够处理不确定性下的决策。
微积分代写
微积分,最初被称为无穷小微积分或 “无穷小的微积分”,是对连续变化的数学研究,就像几何学是对形状的研究,而代数是对算术运算的概括研究一样。
它有两个主要分支,微分和积分;微分涉及瞬时变化率和曲线的斜率,而积分涉及数量的累积,以及曲线下或曲线之间的面积。这两个分支通过微积分的基本定理相互联系,它们利用了无限序列和无限级数收敛到一个明确定义的极限的基本概念 。
计量经济学代写
什么是计量经济学?
计量经济学是统计学和数学模型的定量应用,使用数据来发展理论或测试经济学中的现有假设,并根据历史数据预测未来趋势。它对现实世界的数据进行统计试验,然后将结果与被测试的理论进行比较和对比。
根据你是对测试现有理论感兴趣,还是对利用现有数据在这些观察的基础上提出新的假设感兴趣,计量经济学可以细分为两大类:理论和应用。那些经常从事这种实践的人通常被称为计量经济学家。
Matlab代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。