MY-ASSIGNMENTEXPERT™可以为您提供caltech Math121a Combinatorics组合学的代写代考和辅导服务!
这是加州理工学院组合学课程的代写成功案例。
Math121a课程简介
Math 121 is our standard three-term course on combinatorics though we are only able to offer two terms this year. The first term covers “structural” combinatorics, the study of interesting discrete structures, both in terms of general properties as well as in terms of the existence or classification of particularly nice or extreme instances. We will spend much of the term on graphs and related topics such as Ramsey theory, with the remainder of the term spent covering other important structures Latin squares, codes, designs, finite geometries, etc.. The second term will cover more quantititative aspects of combinatorics, as well as applications to and from algebra.
Prerequisites
Grades: Grades will be assessed on the basis of homeworks, which will be given roughly biweekly. There will be no exams (or midterms). Students may discuss problems with each other but have to write down the solutions independently.
The following restrictions hold for all problems of the set: Students may ask questions to the TA (if one exists) and the professor. Resources which you may use while working on the homework include any books and non-interactive websites (i.e. no posting of the questions on internet fora). For calculations which you can do by hand, you may use a computer algebra program Mathematica, Maple, etc.; you may also fell free to use a computer to gain intuition say by solving small instances of the problems, so long as your eventual proof does not depend on such a computation. If you use significant ideas from any source, other than the books mentioned on this website, you should mention where you got them from.
Math121a Combinatorics HELP(EXAM HELP, ONLINE TUTOR)
We are interested in forming 3 letter words (“3-words”) using the letters in LITTLEST. For the purposes of the problem, a “word” is any ordered list of letters.
(a) How many words can be made with no repeated letters?
(b) How many words can be made with unlimited repetition allowed?
(c) How many words can be made if repeats are allowed but no letter can be used more often than it appears in LITTLEST?
(a) Since there are 5 distinct letters, the answer is $5 \times 4 \times 3=60$.
(b) Since there are 5 distinct letters, the answer is $5^3=125$.
(c) Either the letters are distinct OR one letter appears twice OR one letter appears three times. We have seen that the first can be done in 60 ways. To do the second, choose one of L and T to repeat, choose one of the remaining 4 different letters and choose where that letter is to go, giving $2 \times 4 \times 3=24$. To do the third, use T. Thus, the answer is $60+24+1=85$.
Redo the previous exercise for $k$-words. The last part should be starred. It can be done if you treat each value of $k \leq 8$ separately and carefully break it down into cases with OR. Even so, you should study the next section before you attempt it.
For (a) we have $5 \times 4 \times \cdots \times(6-k)$. For (b) we have $5^k$. For (c) we omit the details, just noting
$\begin{array}{lll}\text { For } k=1, \text { there are } 5 . & \text { For } k=2, \text { there are } 7 . & \text { For } k=4 \text {, there are } 286 . \ \text { For } k=5, \text { there are } 820 . & \text { For } k=6, \text { there are 1920. } & \text { For } k=7 \text {, there are } 3360 . \ \text { For } k=8, \text { there are } 3360 . & \text { For } k>8, \text { there are none. } & \end{array}$
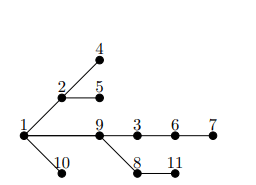
Each of the following belongs to one of the four types of things described in Example 1.13. In each case, list the other three things that correspond to it using the correspondences in the example.
(a) 1122112122
(b) $(a(b c))(((d e) f) g)$
(c)
(a) push, push, pop, pop, push, push, pop, push, pop, pop. Remembering to start with something, say $a$ on the stack: $(a(b c))((d e) f)$.
(b) This is almost the same as (a). The sequence is 112211212122 and the last “pop” in (a) is replaced by “push, pop, pop.”
(c) $a((b((c d) e))(f g))$; push, push, push, pop, push, pop, pop, push, push, pop, pop, pop; 111010011000 .
Suppose we have an election as in Example 1.13 , but now the first candidate is always ahead except for the $0-0$ and $n-n$ ties at the start and finish. How many ways can this happen?
If we remove the first vote (which must be for the first candidate) and the last vote (which must be for the second candidate), we now have an election where ties are allowed but each candidate receives only $n-1$ votes. Thus the answer is $C_{n-1}$.

MY-ASSIGNMENTEXPERT™可以为您提供CALTECH MATH121A COMBINATORICS组合学的代写代考和辅导服务!